Аксиоматическое построение системы натуральных чисел
ТЕМА 1
АКСИОМАТИЧЕСКОЕ ПОСТРОЕНИЕ СИСТЕМЫ
НАТУРАЛЬНЫХ ЧИСЕЛ
Цель: Проверить знание понятий данной темы (аксиоматическое определение системы натуральных чисел, число как элемент натурального ряда), отношения «меньше», четырех арифметических действий, отрезка натурального ряда, конечного множества, числа элементов множества, счета, применять знания и умения для решения практических задач.
Задания к тестам: выделить желтым цветом правильные ответы; дать обоснование правильных ответов. В обосновании сформулировать в теоретических заданиях определение, теорему, указать номер теоремы, пункт и стр. учебника, в практических решение, используя метод. рекоменд. К контрольной работе. Обоснование дать к каждому тестовому заданию.
Ф.И.О. Барсукова Евгения Александровна
Группа: ОБ-РНО-11
1 Утверждения, которые принимаются без доказательства,
называются:
a) определениями
b) теоремами
c) аксиомами
d) примерами
e) высказываниями
Обоснование: аксиомы – предложения, которые в данной теории принимаются без доказательства; в них раскрываются свойства основных понятий. П.59, С.232.
2 Требования, предъявляемые к системе аксиом:
a) полнота, монотонность, независимость
b) непротиворечивость, независимость, полнота
c) независимость, непротиворечивость, монотонность
d) монотонность, полнота, непротиворечивость
e) полнота, монотонность, противоречивость
Обоснование: система аксиом называется непротиворечивой, если из нее нельзя логически вывести два взаимно исключающих друг друга предложения. Непротиворечивая система аксиом называется независимой, если никакая из аксиом этой системы не является следствием других аксиом этой системы. П.59, с.232
3 При аксиоматическом построении системы натуральных чисел элемент, непосредственно следующий за элементом а обозначают:
a) – а
b) 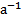
c) 
d) 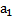
e) - 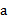
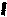 Обоснование: элемент, непосредственно следующий за элементом а, обозначают а (штрих). П.60, с.233
Обоснование: элемент, непосредственно следующий за элементом а, обозначают а (штрих). П.60, с.233
4 Система аксиом Пеано содержит:
a) 2 аксиомы
b) 5 аксиом
c) 3 аксиомы
d) 4 аксиомы
e) 6 аксиом
Обоснование: «сформулированные аксиомы часто называют аксиомами Пеано». П.60, с.233
5 Элементы множества N , для которых установлено отношение «непосредственно следовать за», удовлетворяющие четырем аксиомам Пеано, называются:
a) четными числами
b) нечетными числами
c) положительными числами
d) натуральными числами
e) другой ответ
Обоснование: в качестве основного понятия при аксиоматическом построении арифметики натуральных чисел взято отношение «непосредственно следовать за», заданное на непустом множестве N. Множество N, для элементов которого установлено отношение «непосредственно следовать за», удовлетворяющее аксиомам 1-4, называется множеством натуральных чисел, а его элементы – натуральными числами. П.60, с.233
6 Термин «натуральное число» впервые употребил:
a) Евклид
b) Архимед
c) Пифагор
d) Фалес
e) Боэций
Обоснование: термин «натуральное число» впервые употребил в V в. Римский ученый А.Боэций, который известен как переводчик работ известных математиков прошлого на латинский язык как автор книги «О введении в арифметику», которая до XVI века была образцом для всей европейской математики. Пар.13, с.231
7 Науку, в которой изучаются натуральные числа и действия над ними, называют:
a) алгебра
b) арифметика
c) математика
d) геометрия
e) натурология
Обоснование: теоретическая наука, которая стала изучать числа и действия над ними, получила название «арифметика». Пар.13, с.230
8 Для счета предметов достаточно множества:
a) целых чисел
b) рациональных чисел
c) иррациональных чисел
d) действительных чисел
e) натуральных чисел
Обоснование: Чтобы вести счет, нужна последовательность числительных, которая начинается с единицы и которая позволяет осуществлять переход от одного числительного к другому и столько раз, сколько это необходимо. Нужен отрезок натурального ряда. Пар.14, стр.231; только после того, как человек научился оперировать множествами-посредниками,…, т.е. когда произошло отвлечение от природы элементов множеств-посредников, возникло представление о натуральном числе. Постепенно сложилось и представление о бесконечности множества натуральных чисел (работа «Псаммит»). Пар.13, с.230
9 Ассоциативный закон сложения натуральных чисел выглядит так:
a) 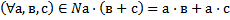
b) 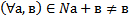
c) 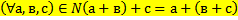
d) 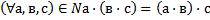
e) 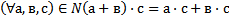
Обоснование: п.61, с.240, теорема 4
10 Действие, с помощью которого находят разность натуральных чисел, называют:
a) уменьшение
b) сложение
c) вычитание
d) деление
e) уменьшаемое
Обоснование: вычитанием натуральных чисел a и b называется операция, удовлетворяющая условию: a-b=c тогда и только тогда, когда b+c=a. П.64, с.249
11 Числа при умножении называются:
a) слагаемые
b) множители
c) делители
d) делимые
e) уменьшаемые
Обоснование: число a*b называется произведением чисел a и b, а сами числа a и b – множителями. П.62, с.243
12 Действие, при помощи которого находят частное натуральных чисел называют:
a) умножением
b) сложением
c) вычитанием
d) делением
e) разностью
Обоснование: делением натуральных чисел a и b называется операция, удовлетворяющая условию: a:b=c тогда и только тогда, когда b*c=a. П.65, с.251
13 Если к множеству натуральных чисел добавить нуль, то получится новое множество, которое называют множеством :
a) целых отрицательных чисел
b) целых положительных чисел
c) множеством положительных чисел
d) целых неотрицательных чисел
e) другой вариант ответа
Обоснование: присоединим к множеству N натуральных чисел еще один элемент, который называется нулем и обозначается 0. Полученное множество называется множеством целых неотрицательных чисел и обозначается Z0. Таким образом, Z0=N 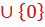 . П.66, с.254
. П.66, с.254
14 Для того чтобы вычесть сумму из числа, достаточно вычесть из этого числа каждое слагаемое последовательно одно за другим. Это правило:
a) деления разности на число
b) деления суммы на число
c) вычитания числа из суммы
d) вычитания разности из числа
e) вычитания суммы из числа
Обоснование: п.64, с.250, теорема 22
15 Чтобы узнать, на сколько одно число меньше или больше другого, надо:
a) из большего числа вычесть меньшее
b) к большему числу прибавить меньшее
c) большее число разделить на меньшее
d) меньшее число умножить на какое-нибудь натуральное число
e) большее число умножить на меньшее
Обоснование: п.64, с.249, теорема 19
16 Запишите, используя символику, правый дистрибутивный закон умножения относительно сложения для натуральных чисел:
a) 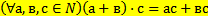
b) 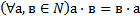
c) 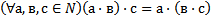
d) 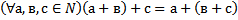
e) 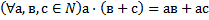
Обоснование: п.62, с.244, теорема 8
1 При делении целых неотрицательных чисел на число 7 могут получиться остатки:
f) 1, 2, 3, 4, 5, 6, 7
g) 0, 1, 2, 3, 4, 5, 6
h) 1, 2, 3
i) 1, 3, 5, 7
j) 0, 1, 2, 3, 4, 5, 6, 7
Обоснование: пусть а – целое неотрицательное число, а b – число натуральное. Разделить а на b с остатком – это значит найти такие целые неотрицательные числа q и r, что а=bq+r, причем 0≤r 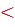 b. П.66, с.255
b. П.66, с.255
17 Как изменится сумма двух натуральных чисел, если каждое из двух слагаемых увеличить в 2 раза
a) Увеличится в 4 раза
b) Увеличится на 2 раза
c) Увеличится на 4 раза
d) Увеличится в 2 раза
e) Другой ответ
Обоснование: п.62, с.244, теорема 8; т.е. было а+b=с. Стало: 2*а+2*b=с, следовательно 2(а+b)=с, значит стало 2с – увеличится в 2 раз.
18 Число а при делении на 8 дает в остатке 3 и поэтому имеет вид:
a) 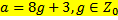
b) 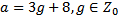
c) 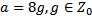
d) 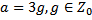
e) 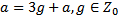
Обоснование: по определению: пусть а – целое неотрицательное число, а b – число натуральное. Разделить а на b с остатком – это значит найти такие целые неотрицательные числа q и r, что а=bq+r, причем 0≤r 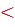 b. П.66, с.255
b. П.66, с.255
19 Для того, чтобы существовало частное двух натуральных чисел a и b , необходимо, чтобы
a) 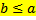
b) 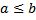
c) 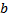
d) 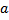
e) другой ответ
Обоснование: п.65, с.252, теорема 23
20 Множество N при помощи отношения «иметь один и тот же остаток при делении на 6» разбивается на
a) 5 классов
b) 2 класса
c) 6 классов
d) 3 класса
e) другой ответ
Обоснование: основываемся на определение п.66, с.255, где 0≤r 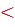 b, значит, при делении на 6 будет 6 остатков: 0,1,2,3,4,5, следовательно, данное множество разбивается на 6 классов
b, значит, при делении на 6 будет 6 остатков: 0,1,2,3,4,5, следовательно, данное множество разбивается на 6 классов
21 Свойство транзитивности отношения «меньше» на множестве натуральных чисел записывается так:
a) Для любых натуральных чисел a,b,c, если a<b и b<c, то a<c
b) Для любых натуральных чисел a,b, если a<b, то неверно, что в<а
c) Для любых натуральных чисел a, неверно, что a<a
d) Для любых натуральных чисел a,b, a<b или b<a
e) Для любых натуральных чисел a,b, если a<b, то b<a
Обоснование: п.63, с.246, теорема 13
22 Если при делении с остатком числа а на 15 получили неполное частное 10, то наибольшее возможное значение делимого:
a) 150 d) 165
b) 160 e)151
c) 164
Обоснование: по определению: пусть а – целое неотрицательное число, а b – число натуральное. Разделить а на b с остатком – это значит найти такие целые неотрицательные числа q и r, что а=bq+r, причем 0≤r 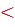 b. П.66, с.255. Найдем наибольшее значение делимого, т.е. а: если b=15, q=10, а остаток r находится в промежутке 0≤r
b. П.66, с.255. Найдем наибольшее значение делимого, т.е. а: если b=15, q=10, а остаток r находится в промежутке 0≤r 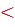 15, значит, наибольший остаток 14, отсюда следует: а=15*10+14=164, ч.т.д.
15, значит, наибольший остаток 14, отсюда следует: а=15*10+14=164, ч.т.д.
23 Законы сложения натуральных чисел в аксиоматической теории доказываются:
a) методом от противного
b) методом полной индукции
c) с использованием дедуктивного вывода
d) методом математической индукции
e) другой ответ
Обоснование: п.67, с.257, пример 1. Метод доказательства, основанный на теореме 30 (п.67, с.257), называется методом математической индукции.
24 Если А(1) и (А(k) => А(k+1)) – истинное высказывание, то делают вывод о том, что утверждение А (n) истинно для любого натурального числа n. Так формулируется:
a) дедуктивный вывод
b) метод математической индукции
c) метод полной индукции
d) закон контрапозиции
e) другой ответ
Обоснование: п.67, с.257, теорема 30
25 Если делимое и делитель умножить на n, то частное:
a) увеличится в n раз
b) не изменится
c) уменьшится в n раз
d) увеличится на n
e) уменьшится на n
Обоснование: делением натуральных чисел а и b называется операция, удовлетворяющая условию: а:b=с тогда и только тогда, когда b*с=а (п.65, с.251). а:b=с. (а*n) : (b*n)= с*n, т.к. по определению b*с=а, значит bn*cn=an, так как число, на которое умножали, одинаковое и если сократить на n, то выйдет изначальное равенство b*с=а, значит частное ее изменится
26 Метод математической индукции состоит:
a) из четырех частей
b) из одной части
c) из пяти частей
d) из двух частей
e) из n частей
Обоснование: п.67, с.257
27 Деление является алгебраической операцией на множестве:
a) натуральных чисел
b) целых неотрицательных чисел
c) целых чисел
d) иррациональных чисел
e) рациональных чисел
Обоснование: Рациональные числа — это целые и дробные числа (обыкновенные дроби, конечные десятичные дроби и бесконечные периодические дроби).
28 Множество натуральных чисел – упорядоченное множество, так как отношение «меньше» для натуральных чисел:
a) транзитивно и симметрично
b) является отношением эквивалентности
c) рефлексивно и симметрично
d) рефлексивно и транзитивно
e) транзитивно и антисимметрично
Обоснование: п.63, с.247
29 Разность натуральных чисел а-b существует только тогда, когда
a) 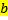
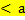 c)
c) 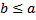 e) другой ответ
e) другой ответ
b) 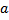 d)
d) 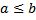
Обоснование: п.64, с.249, теорема 19
30 Одним из основных (неопределяемых) понятий математики является:
a) теорема
b) квадрат
c) умозаключение
d) индукция
e) множество
Обоснование: множество – те или иные группы объектов, рассматриваемые как единое целое: натуральные числа, треугольники, квадраты и т.д. (пар.1, п.1, с.7)
31 При делении на 7 чисел a и b получаются остатки 2 и 5. тогда произведение ab при делении на 7 дает остаток:
a) 10 c) 2 e) 7
b) 3 d) 5
Обоснование: Числа можно представить так:
первое - (7a+2)
второе - (7b+5), где a и b некоторые целые натуральные числа
7a и 7b - целая часть чисел, которая делится на 7
2 и 5 - соответственно остатки. Тогда их произведение (7a+2)(7b+5) = 49ab + 35a + 14b + 10. Из получившегося выражения видим, что первые три слагаемых делятся на 7 при любых натуральных a и b, остается 10, которое при делении на 7 дает остаток 3 - это и есть искомый остаток. При делении произведения этих чисел остаток будет равен 3.
32 Не выполняя вычислений выясните значения каких выражений будут равны
a) (50+16)-14 и 50+(16-14)
b) (50+16)-14 и 50-(16-14)
c) (50+16)-14 и (50-16)+14
d) (50+16)-14 и (50-14)-16
e) (50+16)-14 и 50-(16+14)
Обоснование: п.64, с.250, теорема 21, под б): для того чтобы вычесть число из суммы достаточно вычесть это число из одного слагаемого суммы и к полученному результату прибавить другое слагаемое
33 Если из системы аксиом нельзя логически вывести два взаимно исключающих друг друга предложения, то она называется:
a) полной
b) независимой
c) непротиворечивой
d) противоречивой
e) зависимой
Обоснование: п.59, с.232.
34 Отрезком Na натурального ряда называется
a) множество натуральных чисел, в котором а элементов
b) конечное множество А, где 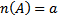
c) множество последовательных натуральных чисел, в котором а элементов
d) множество натуральных чисел, не превосходящих натурального числа а
e) другой ответ
Обоснование: по определению п.68, с.259
35 Если с и d- натуральные числа, то 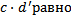
a) 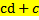 c)
c) 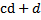 e)
e) 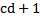
b) 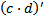 d)
d) 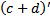
Обоснование: по определению п.62, с.243: умножением натуральных чисел называется алгебраическая операция, обладающая свойствами: 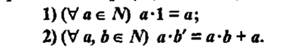 , где из 2 пункта следует аналогично, что
, где из 2 пункта следует аналогично, что 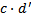 =
= 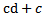
36 Множества А и В называют равномощными, если
a) 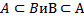
b) Если каждому элементу множества А соответствует элемент множества В
c) Если они равночисленны
d) Между ними можно установить взаимно-однозначное соответствие
e) Другой ответ
Обоснование: п.42, с.172
37 Числа возникли из потребности:
a) счета
b) измерения
c) количественной характеристики элементов конечного множества
d) измерения положительных скалярных величин
e) счета и измерения
Обоснование: пар.13, с.229: числа возникли из потребности счета и измерения и претерпели длительный путь исторического развития.
38 Отношение «непосредственно следовать за», заданное на множестве натуральных чисел, обладает свойством
a) Транзитивности
b) Рефлексивности
c) Антисимметричности
d) Связанности
e) Симметричности
Обоснование: отношение R на множестве Х называется антисимметричным, если для различных элементов х и у из множества Х выполнено условие: из того, что х находится в отношении R с элементом у, следует, что элемент у в отношении R c элементом х не находится. 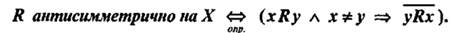 (п.60, с.234, где описывается суть отношения «непосредственно следовать за»)
(п.60, с.234, где описывается суть отношения «непосредственно следовать за»)
39 Множество целых неотрицательных чисел упорядочивает отношение
a) «непосредственно следовать за»
b) «меньше»
c) «равно»
d) «непосредственно предшествовать»
e) «больше на 2»
Обоснование: п.66, с.254: «Присоединим к множеству N натуральных чисел еще один элемент, который называется нулем и обозначается 0. Полученное множество называется множеством целых неотрицательных чисел и обозначается Z0. Таким образом, Z0=N 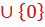 . Относительно числа 0 условимся, что оно меньше любого натурального числа, а арифметические операции, в случае, когда одна из компонентов равна нулю, определяются равенствами»
. Относительно числа 0 условимся, что оно меньше любого натурального числа, а арифметические операции, в случае, когда одна из компонентов равна нулю, определяются равенствами»
40 Если делимое увеличить в 48 раз, а делитель в 6 раз, то частное
a) увеличится на 42 раза
b) уменьшится в 8 раз
c) уменьшится на 42
d) увеличится в 8 раз
e) увеличится на 8
Обоснование: делением натуральных чисел а и b называется операция, удовлетворяющая условию: а:b=с тогда и только тогда, когда b*с=а (п.65, с.251) Из основных свойств деления знаем, что если увеличить (или уменьшить) делимое в несколько раз, то частное увеличится (или уменьшится) во столько же раз и если увеличить (или уменьшить) делитель в несколько раз, то частное уменьшится (или увеличится) во столько же раз, значит соответственно: если записать частное в виде равенства a : b = c, то изложенное свойство частного можно записать так: (a · m) : b = c · m и (a : m) : b = c : m и если a : b = c, то (a · m) : (b · m) = c и (a : m) : (b : m) = c. Значит:
Если делимое увеличить в 48 раз, то частное увеличится в 48 раз.
Если делитель увеличить в 6 раз, то частное уменьшится в 6 раз.
Таким образом, если проделать оба эти действия, то частное увеличится в 8 раз, так как 48 кратно 6.
41 Если уменьшаемое уменьшить на 3, а вычитаемое увеличить на 3, то разность
a) не изменится
b) уменьшится на 6
c) увеличится на 6
d) уменьшится на 3
e) увеличится на 3
Обоснование: вычитанием натуральных чисел а и b называется операция, удовлетворяющая условию: а-b=c тогда и только тогда, когда b+с=а (п.64, с.249). (a-3) – (b+3) = a-3-b-3 = (a-b) – 6 = c - 6
42 Какой цифрой заканчивается сумма
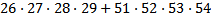
a) 9 c) 8 e) 7
b) 0 d) 4
Обоснование: сложением натуральных чисел называется алгебраическая операция, обладающая свойствами: 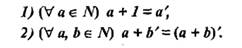 (п.61, с.237)
(п.61, с.237)
умножением натуральных чисел называется алгебраическая операция, обладающая свойствами: 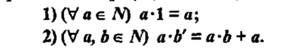 (п.62, с.243)
(п.62, с.243)
Перемножив только единицы, получим, что каждое из двух произведений слева (6*7*8*9=3024) и справа (1*2*3*4=24) оканчивается цифрой 4, поэтому вся сумма оканчивается цифрой 8. (4+4=8)
43 Какой цифрой заканчивается разность
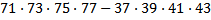
a) 4 c) 9 e)3
b) 5 d) 6
Обоснование: вычитанием натуральных чисел a и b называется операция, удовлетворяющая условию: a-b=c тогда и только тогда, когда b+c=a. П.64, с.249
умножением натуральных чисел называется алгебраическая операция, обладающая свойствами: 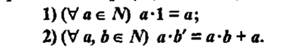 (п.62, с.243)
(п.62, с.243)
Перемножив только единицы, получим, что произведение слева (1*3*5*7=105) и справа (7*9*1*3=189) оканчивается цифрой 5 и 9 соответственно, при этом первое произведение больше второго.5+9=16, под единицами стоит цифра 6, значит разность оканчивается цифрой 6.
44 Если каждый из двух множителей увеличить в 3 раза, то произведение
a) увеличится в 3 раза
b) не изменится
c) увеличится в 9 раз
d) увеличится на 9
e) увеличится на 3
Обоснование: умножением натуральных чисел называется алгебраическая операция, обладающая свойствами: 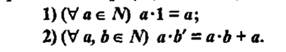 (п.62, с.243)
(п.62, с.243)
а*b=с
3а*3b=9с, так как 9(а*b)=9с (п.62, с.245. теорема 9), и если сократить на 9, то вернемся к искомому выражению а*b=с. Что означает, что произведение действительно увеличится в 9 раз.
45 Если уменьшаемое увеличить в 4 раза и вычитаемое увеличить в 4 раза, то разность
a) Увеличится в 8 раз
b) Увеличится в 4 раза
c) Не изменится
d) Увеличится в 16 раз
e) Увеличится на 8
Обоснование: умножением натуральных чисел называется алгебраическая операция, обладающая свойствами: 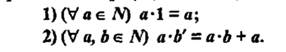 (п.62, с.243)
(п.62, с.243)
вычитанием натуральных чисел a и b называется операция, удовлетворяющая условию: a-b=c тогда и только тогда, когда b+c=a. П.64, с.249
а-b=c. (а*4) – (b*4) = 4(а-b), следовательно, разность увеличится в 4 раза.
46 Если число а при делении на 5 дает в остатке 1, то число а2 при делении на 5 дает в остатке
a) 0 c) 3 e) 1
b) 2 d) 4
Обоснование: делением натуральных чисел a и b называется операция, удовлетворяющая условию: a:b=c тогда и только тогда, когда b*c=a. П.65, с.251
Число a:5 можно записать в виде 5n+1, значит а2:5 можно записать как (5n+1)2=25n2+5n+1. 25n2+5n делится на 5 без остатка, значит 1 – остаток.
47 В аксиоматической теории свойство антисимметричности отношения «меньше» доказывается
a) Методом от противного
b) С помощью дедуктивного вывода
c) Методом математической индукции
d) Методом полной индукции
e) На основе закона контрапозиции
Обоснование: п.63. с. 246, теорема 14.
48 В аксиоматической теории свойство транзитивности отношения «меньше» доказывается
a) С помощью дедуктивного вывода
b) Методом математической индукции
c) Методом от противного
d) Методом полной индукции
e) На основе закона контрапозиции
Обоснование: п.63, с.246, теорема 13
49 При доказательстве того, что деление на нуль невозможно рассматривается
a) Два случая d) Несколько частных случаев
b) Один случай e) Другой ответ
c) Три случая
Обоснование: п.66, с.254, теорема 28.
50 Как называется число b в равенстве a : b = c
a) Вычитаемое c) Делитель e) Разность
b) Делимое d) Частное
Обоснование: число а:b называется частным чисел а и b, число а – делимым, число b – делителем. П.65, с.252
51 Как называется число а в равенстве 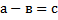
a) Уменьшаемое c) Вычитаемое e) Другой ответ
b) Делимое d) Разность
Обоснование: число а-b называется разностью чисел а и b, число а – уменьшаемым, а число b – вычитаемым. П.64, с.249.
52 Какое свойство неявно используют младшие школьники при выполнении задания 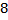
a) Коммутативное свойство сложения
b) Свойство монотонности сложения
c) Свойство сократимости сложения
d) Ассоциативное свойство сложения
e) Другой ответ
Обоснование: п.63, с.248: «С отношением "меньше"("больше") для натуральных чисел младшие школьники знакомятся в самом начале обучения. И часто, наряду с его теоретико- множественной трактовкой, неявно используется определение, данное нами в рамках аксиоматической теории. Например, учащиеся могут объяснить , что 9> 7 , так как 9 - это 7+2. Нередко и неявное использование свойств монотонности сложения и умножения. Например, дети объясняют, что " 6+2< 6+3, так как 2 <3»
53 Первая аксиома Пеано формулируется так:
a) В множестве N существует элемент, непосредственно не следующий ни за каким элементом этого множества. Называют его единицей
b) Для каждого элемента а из N существует единственный элемент а´, непосредственно следующий за а.
c) Пусть множество М есть подмножество множества N и известно, что единица содержится в М; и из того, что а содержится в М, следует, что и а´ содержится в М. Тогда множество М совпадает с множеством N.
d) Прямая разделяет плоскость на две полуплоскости.
e) Для каждого элемента а из N существует не более одного элемента, за которым непосредственно следует а.
Обоснование: п.60, с.233
54 Четвертая аксиома Пеано формулируется так:
a) Пусть множество М есть подмножество множества N и известно, что: единица содержится в М; и из того, что а содержится в М, следует, что и а´ содержится в М. Тогда множество М совпадает с множеством N.
b) Для каждого элемента а из N существует не более одного элемента, за которым непосредственно следует а.
c) Прямая разделяет плоскость на две полуплоскости.
d) В множестве N существует элемент, непосредственно не следующий ни за каким элементом этого множества. Называют его единицей.
e) Для каждого элемента а из N существует единственный элемент а´, непосредственно следующий за а.
Обоснование: п.60, с.233
55 Используя определение умножения натуральных чисел в аксиоматической теории, найдите значение выражения 3*7
a) 3*7=3*(10-3)=3*10-3*3=30-9=21
b) 3*7=3+3+3+3+3+3+3=21
c) 3*7=7+7+7=21
d) 3*7=3*(5+2)=3*5+3*2=15+6=21
e) 3*7=3*6’=3*6+3=18+3=21
Обоснование: умножением натуральных чисел называется алгебраическая операция, обладающая свойствами: 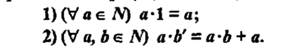 (п.62, с.243, 2 свойство)
(п.62, с.243, 2 свойство)
56 Установление взаимно однозначного соответствия между элементами непустого конечного множества А и отрезком натурального ряда называется
a) Теоретико-множественной характеристикой множества А
b) Классом конечных равномощных множеств
c) Отношением порядка на множестве А
d) Счетом элементов множества А
e) Другой ответ
Обоснование: по определению п.68, с.260
57 В аксиоматической теории разностью натуральных чисел а и в называется натуральное число c, удовлетворяющее условию:
a) в+с=а
b) 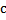
c) а+с=в
d) 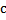
e) другой ответ
Обоснование: вычитанием натуральных чисел a и b называется операция, удовлетворяющая условию: a-b=c тогда и только тогда, когда b+c=a. П.64, с.249
58 Запишите, используя символику, коммутативный закон сложения для натуральных чисел:
a) 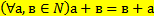
b) 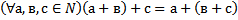
c) 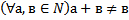
d) 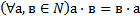
e) 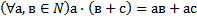
Обоснование: п.61, с.241, теорема 5
59 Запишите, используя символику, ассоциативный закон умножения для натуральных чисел:
a) 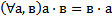
b) 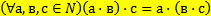
c) 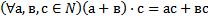
d) 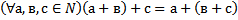
e) Для любых натуральных чисел a, b, c, 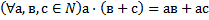
Обоснование: п.62, с.245, теорема 10
60 Не выполняя вычислений, определите значения каких выражений будут равны
a) 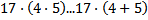
b) 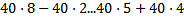
c) 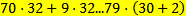
d) 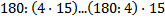
e) 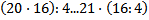
Обоснование: Если вынести с левой части уравнения общий множитель, получаем 32⋅(70+9)=79⋅(30+2), если упростить выражение, то получится 32*79=79*32, а это коммутативный закон умножения, следовательно они равны.
61 Сложением натуральных чисел называется алгебраическая операция, обладающая двумя свойствами, второе свойство записывается так
a) Для любых натуральных чисел а и в 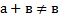
b) Для любых натуральных чисел а и в 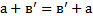
c) Для любых натуральных чисел а и в 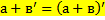
d) Для любых натуральных чисел а и в 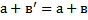
e) другой ответ
Обоснование: сложением натуральных чисел называется алгебраическая операция, обладающая свойствами: 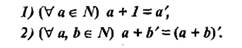 (п.61, с.237)
(п.61, с.237)
62 При аксиоматическом построении системы натуральных чисел в качестве основного взято отношение:
a) «следовать за»
b) «непосредственно следовать за»
c) «непосредственно предшествовать»
d) «предшествовать»
e) другой ответ
Обоснование: п.60, с.233 «В качестве основного понятия при аксиоматическом построении арифметики натуральных чисел взято отношение «непосредственно следовать за», заданное на непустом множестве N.»
63 Вторая аксиома Пеано формулируется так:
a) В множестве N существует элемент, непосредственно не следующий ни за каким элементом этого множества. Называют его единицей.
b) Для каждого элемента а из N существует не более одного элемента, за которым непосредственно следует а.
c) Пусть множество М есть подмножество множества N и известно, что единица содержится в М; и из того, что а содержится в М, следует, что и а’ содержится в М. Тогда множество М совпадает с множеством N
d) Для каждого элемента а из N существует единственный элемент а’, непосредственно следующий за а.
e) Прямая разделяет плоскость на две полуплоскости
Обоснование: п.60, с.233
64 В аксиоматической теории отношение «меньше» определено следующим образом:
a) 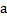
b) 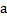
c) 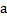
d) 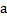
e) другой ответ.
Обоснование:
65 Отношение «меньше» на множестве натуральных чисел обладает свойствами:
a) Рефлексивность, симметричность и транзитивность;
b) Рефлексивность, антисимметричность и транзитивность;
c) Рефлексивность, антисимметричность и связанность;
d) Антисимметричность, транзитивность и связанность;
e) Симметричность, антисимметричность и транзитивность.
Обоснование: п.63, с.246 теорема 12 - свойство связанности отношения «меньше»; теорема 13 - свойство транзитивности отношения «меньше»; теорема 14 - свойство антисимметричности отношения «меньше»
66 Умножением натуральных чисел называется алгебраическая операция, определенная на множестве натуральных чисел и обладающая двумя свойствами, второе свойство записывается так
a) Для любых натуральных чисел а и в а·в'=ав+а
b) Для любых натуральных чисел а и в а·в'=(а·в)'
c) Для любых натуральных чисел а и в а·в'=ав+а
d) Для любых натуральных чисел а и в а·в'=(а·в)'
e) Для любых натуральных чисел а и в а·в'=ав+в
Обоснование: по определению п.62, с.243: умножением натуральных чисел называется алгебраическая операция, обладающая свойствами: 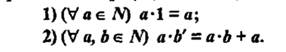 ,
,
67 Назовите в порядке выполнения преобразований свойства сложения, которые используются при нахождении значения выражения 23+(19+7)=23+(7+19)=(23+7)+19=30+19=49
a) коммутативное свойство сложения и дистрибутивность слева относительно сложения
b) ассоциативное свойство сложения и коммутативное свойство сложения
c) дистрибутивность справа относительно сложения и ассоциативное свойство сложения
d) коммутативное свойство сложения и ассоциативное свойство сложения
e) дистрибутивность слева относительно сложения и коммутативное свойство сложения
Обоснование: п.61, с.241 сначала была выполнена теорема 5, затем теорема 4 с.240: a+(b+c)=a+(c+b)=(a+c)+b
68 Отрезком натурального ряда N4 является множество:
a) {1,3,5,7} c) {1,2,3,4} e) {10,11,12,13}
b) {2,3,4,5} d) {1,2,4,5}
Обоснование: п.68, с.259 по определению: отрезком Nа натурального ряда называется множество натуральных чисел, не превосходящих натурального числа а. Таким образом, если у нас задано N4 , значит множество будет состоять из {1,2,3,4}
69 Из перечисленных свойств множества натуральных чисел выделите свойство дискретности:
a) Из всех натуральных чисел единица является наименьшим числом.
b) Ни для одного натурального числа а нет такого натурального числа n, что а<n<а+1
c) Множество натуральных чисел – упорядоченное множество, т.к. отношение «меньше» для натуральных чисел транзитивно и антисимметрично
d) Множество натуральных чисел бесконечно
e) Любое непустое подмножество множества натуральных чисел содержит наименьшее число.
Обоснование: п.63, с.248: «Ни для одного натурального числа а не существует такого натурального числа что а<n<а+1. Это свойство называется свойством дискретности множества натуральных чисел».
70 На множестве натуральных чисел алгебраической является операция:
a) Пересечение c) Вычитание e) Сложение
b) Деление d) Объединение
Обоснование: п.61, стр.237 - по определению: сложением натуральных чисел называется алгебраическая операция, обладающая некоторыми свойствами
71 Если один из множителей увеличить в 5 раз, а второй уменьшить в 5 раз, то произведение
a) Увеличится в 5 раз
b) Не изменится
c) Уменьшится в 5
d) Увеличится в 25 раз
e) Уменьшится в 25
Обоснование: по свойству произведения: если уменьшить/увеличить множимое или множитель в несколько раз, то и произведение уменьшится/увеличится во столько же раз. В нашем случае сначала произведение увеличилось в 5 раз, так как один из множителей увеличили в 5 раз, затем уменьшилось в 5 раз, так как второй множитель уменьшили в 5 раз, следовательно, произведение осталось прежним: (5*a)*b=5c; (5*a)*(b:5)=с (так как 5 и 1/5 сократятся при умножении)
72 Третья аксиома Пеано формулируется так:
a) Прямая разделяет плоскость на две полуплоскости
b) Для каждого элемента а из N существует единственный элемент а', непосредственно следующий за а.
c) Пусть множество М есть подмножество множества N и известно, что: единица содержится в М и из того, что а содержится в М, следует, что и а' содержится в М. Тогда множество М совпадает с множеством N.
d) Для каждого элемента а из N существует не более одного элемента, за которым непосредственно следует а..
e) В множестве N существует элемент, непосредственно не следующий ни за каким элементом этого множества. Называют его единицей.
Обоснование: п.60, с.233
73 Назовите в порядке выполнения преобразований свойства, которые используются при нахождении значения выражения 17·25+75·17=17·25+17·75=17·(25+75)=17·100=1700
a) коммутативное свойство умножения и дистрибутивность слева относительно сложения
b) коммутативное свойство сложения и дистрибутивность слева относительно сложения
c) ассоциативное свойство умножения и коммутативное свойство умножения
d) дистрибутивность справа относительно сложения и ассоциативное свойство умножения
e) дистрибутивность слева относительно сложения и коммутативное свойство умножения
Обоснование: п.62, с.245 сначала была выполнена теорема 11, затем теорема 9: a*b+c * a=a*b+a * c=a*(b+c)
74 Законы умножения натуральных чисел в аксиоматической теории доказываются:
a) методом полной индукции
b) методом от противного
c) методом математической индукции
d) с использованием дедуктивного вывода
e) другой ответ
Обоснование: п.67, с.257: Метод доказательства, который основан на аксиоме 4(с.254) можно использовать при доказательстве свойств сложения и умножения, можно применять и для доказательства других утверждений о натуральных числах.








