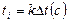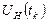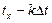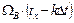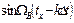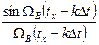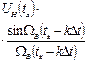Дискретезация кемшіліктерін анықтау және узіліссіз сигналдарды қалпына келтіру
1.1Котельников В.А. теоремасы: Дискреттік үзіліссіз сигналдар
Б.з.б 30 жылдарында дискреттік үзіліссіз сигналдардың теориясы мен практикасына қызығушылық көбейді. Қызығушылық пайда болғаны, дискреттік арқылы екі ұтыс аламыз: кедергілермен айналдыру үзіліссіз сигналды (сурет 1) және мезгілдік тығыздықтың байланыс жолын жасау. Мәліметті бірнеше бастаулардан бір линиядан жіберу, бізге жоғары экономикалық нәтиже береді. Мезгілдік тығыздықты (сурет 2) көреміз. Котельников дискретезацияны зерттеп оның теориясы негіздеп, өзінің иатақты теориясын дәлелдеді.
|
|
|
|
|

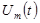
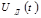
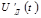
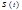
|
|
|
 1 2 3 4 5
1 2 3 4 5 

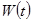
|
| ||||||
|
| ||||||
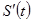
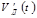

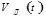
 |  |  |  |  | |||||||
 | |||||||||||
6 7 8 9 10 
|
|
 11
11
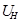

 б)
б)  1 0 1 0 д)
1 0 1 0 д)








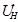
в) е)  1 0 1 0
1 0 1 0




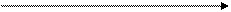
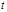

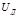
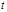
ж) 1 0 1 0

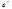 )
)





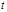

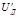
 г)
г)
|
|
0 0

1-сурет
Сурет1 Дискреттік үзіліссіз сигналдардың беріліс жүйесі
а) үлгілі жүйесі мезгілдік диаграманың туйіншіктерінде
б ) в т т 2││ в ) дискретизатор ішінде уақыт бойынша дискретизация
г)в т т 4,9 д) в т т 5,8 мс амплитудалық модуляциямен
е ) в т т 6 ж ) в т 7
ИС1 ОС1 ВФ1
|
|
|
П1
 | |||||||
 |  | ||||||
 | |||||||
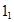
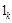
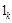
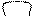
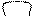 ИС2 ОС2 ВФ2
ИС2 ОС2 ВФ2
|
|
|
|


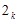

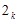 П2
П2




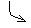
. .


 .ИСN ОСN . ВФN
.ИСN ОСN . ВФN
|
|
|
 .
. 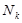
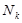
ПN
2-сурет
2-сурет.Уақытша тығыздалуымен және үздіксіз сигнал көздерімен берлген N каналды байланыс жүйесі
 | |||
 | |||
 |
 Б
Б
 | |||
 | |||

 А
А
 |
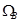
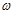
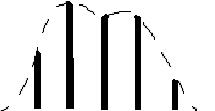
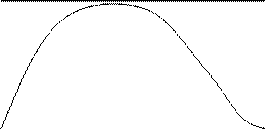
4 сурет
4 сурет .Идеалды ФНЧ(А)ның және шынайы (Б)ның амплитудалық - жиілікті сипаттамасы
«Үздіксіз сигнал, уақыт функциясымен берілген және кейбір fB жиіліктен тұратын құрама жиіліктері жоқ сигнал» өзінің есебімен анықталатын, уақыт интервалына тең At арқылы алынған мәнімен анықталады.
At=1/2 fB
Бұл жерде, fB – спектр сигналының жоғарғы жиілігі.
Бұл теорема дискреттік арна арқылы үздіксіз сигналдың жеткізілуін , қабылдауда оның қалыпқа келуін және электро байланыс жолын уақытша тығыздалу мүмкіндігін дәлелдейді.
Дискреттелетін үздіксіз сигналға арналған теоремаға автордың шектеуі (fB гармоникалық құраманың болмауы) оның практикалық қолданылуын мүлде шектемейді. Телефондық арналарда сөйлеу сигналы, спектрі 12-15 кГц болатын, 3кГц жиілік жолағы апарылады: радиохабарлауда бір арнаға 10кГц апарылады, сол сияқты музыкалық жеткізулер жаңғыртуын бұрмалаусыз жеткізуге арнаны қалдыруға екі есе кең жиілікті қажет етеді.
Котельников бойынша дискретизацияның қорытындысы болып, ортагональді функцияның суммасы болатын берілген үздіксіз сигналдың (UH(t)) берілуі, мынадай:
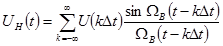
Мұндағы к – жиынның мүшелер саны,
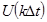 – функцияға ортогональды амплитуда
– функцияға ортогональды амплитуда
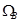 – сигнал спекторының жоғарғы дөңгелек жиілігі:
– сигнал спекторының жоғарғы дөңгелек жиілігі: 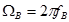
Δt – уақыт бойынша дискреттеу қадамы, В.А.Котельниковтың теоремасы бойынша анықталады.
Сонымен қарастырылып отырған дискреттік үздіксіз сигнал U(t) байланыс тракта кірісте ауыстырылып, келесі Δt үшбұрыштық импульс арқылы аралықта алынады. Бұл келесі кезекте дискреттік сигналға айналуы мүмкін (егер мынадай тапсырма тұрса) онда бұл жағдайда дискретизаторға айналғанда уақытпен екінші операция дәреже арқылы кванторда(бұл 1-ші суретте орнын алып тұр) импульстық амплитуда жатқан дәрежеге айналады.
Бірақ дискретизация орындалып жатқанда В.А.Котельниковтың тапсырмасы тек уақытша каналдармен айналмайды және де үздіксіз дискреттік сигналға дәрежесінде квант болмайды.
Онда, барлық импульстар амплитуда UH(t) мағынасы бойынша есеп нүктесінде (∆t, 2∆t…т.б.) және бұл импульстар бірден модуляторға түседі(бұл жерде көбіне амплитудалық модуляция болады).
 Сонда, сумма белгісі болатын «к» нені білдіреді? Бұл функция мына түрде
Сонда, сумма белгісі болатын «к» нені білдіреді? Бұл функция мына түрде
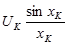 болады да (3 сур.) көсетілген. Төменгі жиілікті (ФНЧ) фильтрлік реакциялар жоғарғы жиілікті fB , бірыңғай тікбұрышты импульс амплитудамен UK тура осындай көрініске ие болады. Тура осындай көрініс ФНЧ да болады (амплитудалық-жиіліктік сипаттамасы АЧХ фильтірі 4 сур. көрсетілген).
болады да (3 сур.) көсетілген. Төменгі жиілікті (ФНЧ) фильтрлік реакциялар жоғарғы жиілікті fB , бірыңғай тікбұрышты импульс амплитудамен UK тура осындай көрініске ие болады. Тура осындай көрініс ФНЧ да болады (амплитудалық-жиіліктік сипаттамасы АЧХ фильтірі 4 сур. көрсетілген).

|
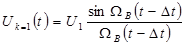
|
|
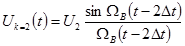
|
|
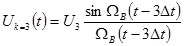
|
|
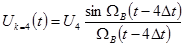
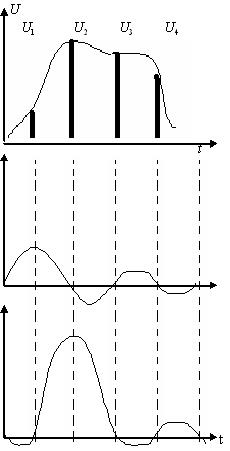
3-сурет
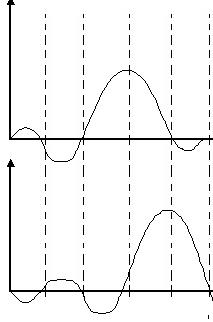
3-сурет. В.А. Котельников бойынша үздіксіз сигналдың дискретизациясы 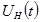 : а)
: а) 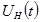 функциясы және В.А. Котельников бойынша импульс. б) І-ыншы импульске ФНЧның реакциясы. в)2-ыншы импульске ФНЧ реакциясы. г)4-ыншы импульске ФНЧ реакциясы.
функциясы және В.А. Котельников бойынша импульс. б) І-ыншы импульске ФНЧның реакциясы. в)2-ыншы импульске ФНЧ реакциясы. г)4-ыншы импульске ФНЧ реакциясы.
Сонымен қатар, егер идеалды ФНЧға (жоғары жиілікті fBдан) В.А. Котельниковтың үздіксіз сигналдарының дискретизациялануы бойынша алынған тізбектелген тікбұрышты импульстерді берсек, онда берілген фильтрдағы реакция суммасы барлық импультерді бермейді V(t), UH(t) ға жақындалған (үш себепке байланысты абсолютті соған тең алу мүмкін емес).
1.2. Үздіксіз сигналдың енгізуде және кванттауда, дискреттеуде пайда болатын қателіктері.
Басымдылық келесі жолдың құндылығымен беріледі: хабар жіберуде қосымша қателіктер енгізіледі, кванттық деңгейдегі және импульс өту кезіндегі есеп арқылы ФНЧ шешіледі.
Бұл қателіктер келесі жағдайда болмаса:В.А.Котельниковтың шексіз ұзындығы аз импульс,шексіз үлкен санына байланысты:қадам квантты(кванттанудағы көрші кезеңдер арасындағы интервал) шексіз кіші шамаға тең, кезеңдер саны шектелмеген шама, ФНЧ (дедискретизатор)-кіршіксіз. Бірақ бұл жағдайлар шындық жүйесінде қатыспаған және ешқашан орындалмайды, сонда көрсетілген қателіктер қайталанбайды.
Шындық шарттар және жүйелер үшін:
Сандық анықтама жүйе мен шешімдердің күрделі мәселесі. Шығыс сигналдарының ∆VH(t) кіріс сигналдарынан ∆UH(t) айырмашылығы бұрмаланудың болу себептеріне байлты.Шығыс сигналын анықтау үшін қателіктерді қарастыра отырып, сонымен қатар онын бұрмалануының көрсете білу. Бастапқы қателіктер жалпы жағдайда былай анықталады:
E0(t)=ƒ[EД(t),EК(t),EФНЧ (t)]
EД(t)- дискреттеу уақыты бойынша сигналдардың бұрмалануы.
EК(t) -деңгей бойынша кезіндегі қателік.
EФНЧ (t)-бұрмалану, қабылдағыштың шығысындағы ФНЧның идеалды емес екенімен шартталған.
Нақты шарттарда және детерминантты сигналды (сынақ үшін алынған сигнал қарастырылып отырған есептеу үшін әдейі таңдалынған математикалық заңның өзгеруі уақыт өте келе белгілі болады) анализденген қателіктер есептеуге беріледі.Осылайша, дискретизация есебінен қателік былай анықталады:
Мұндағы,
∆UH(tх)-нүктедегі сигналдың шындық мәні, tх уақыт осіндегі, UД(tх)-көрсетілген нүктедегі сигналдың мәні, Котельниковтың әдісі бойынша анықталған.
Қателіктердің қосындысы дискретизация есебінен уақыт бойынша және кванттық кезең бойынша,сол формула бойынша анықталады, бірақ ∆UД(tх) табар кезде импульс амплитудасы U(U∆t) қатарға кіретін шынайы емес кванттық кезеңге жақындалып дөңгеленгенін алған дұрыс. Қателікті анықтау үшін, дедискретизатор (ФНЧ) кіргізген келесі жағдайды жасауға болады: мәні арқылы табуға болады.
EФНЧ( t)=1\t0∫[VФНЧ(t)-UН (t)]dt
Мұндағы, UН (t)-байланыс канал кірісіндегі детерминанттық сигнал.
Vфнч(t)- ФНЧ-дан өткен сигналдың уақытша сипаттамасы. Сонғысы мына түрде анықталады (Фурьеның кері қалыптасуының көмегімен):
U( ω )= 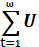 c ( ω 1 )Kфнч (ω1)
c ( ω 1 )Kфнч (ω1)
Мұндағы, 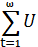 c(ω1) – сигнал көзінен шығу кезіндегі детерминатталған сигнал спектрі.
c(ω1) – сигнал көзінен шығу кезіндегі детерминатталған сигнал спектрі.
Kфнч (ω)- төменгі жиілікті фильтрдің АЧХ.
2. Жұмыстың орындалу тәртібі
2.1 Δt үздіксіз сигнал дискретизациясының интервалын анықтау,мына формуламен (1) анықталады,мұндағы fв=Ωв/2 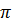 , Ωв берілген.
, Ωв берілген.
2.2 В.А. Котельникова есептеуін анықтау және сол бойынша сигналдың графигін салу.
Бұл үшін сигналдың ұзақтығы (tc) дискретизация интервалына бөледі; осымен В.А. Котельникова есебі кескінделетін уақыт моменті анықталады.
2.3. Кванттауды алып жүргендегі қателікті анықтау.
Оны мына формула бойынша анықтауды: Ek(t)=EД.к(t)-EД(t)
EД.к(t) -уақыт бойынша және деңг ей бойынша кванттауды дикреттеу кезіндегі қателік. Соңғысы EД.к(t) да тура осы жолмен анықталады(EД(t)). Деңгейдің кернеулік жақын мәні алынады. Барлық деңгейдінің кернеулік мәні кванттау деңгейінің номеріне көбейтіледі (jΔa).
Мұндағы, UH(t)max- уақыт бойынша сигналдың кесіндісінің максималдық мәні
n-кванттаудың сандық деңгейі. Деңгейлердің кернеулік мәнін кестеге енгіземіз.
2.4. Қателіктің пайда болу себебін түсіндіру. Қателіктерді ЭВМ-де есептеп көрсету керек.
3. Есептеу бөлімі
Сигнал мына түрде берілген:
ω=π/2 Гц, а=0.6
сигнал спекторы жиілікпен шектелген: Ωв=2π Гц
сигналдың ұзақтығы tc=8c
Барлық есептеулер кестеге енгізіледі.
Кванттау UH(t) лездік мәндерінің (Δt, 2Δt және т.б.) нүктелерінің амплитудасына тең және бұл импульстер дереу модуляторға беріледі,(көбінесе модуляция амплитудасы қолданылады). Осы қосылыста «к» функциясы нені білдіреді? Яғни, (осының орқасында жеңіл түрде тексереміз) функция Uk sinxk/ xk түрінде болады, 3 суретте көрсетілгендей. Бірақ төменгі жиілік фильтр реакциясы жоғарғы жиілік fB бірлік тікбұрышты импульс Uk амплитудасымен берілгендегі реакция түрінде болады. ФНЧ де дәл осы түрде болады.
В.А.Котельников әдісі бойынша үздіксіз сигналдың дискреттелу интервалын анықтау . Мына формула бойынша енгіземіз: ∆t=1/2 ƒB , Гц ƒB=0,3÷3,4
В.А.Котельников әдісі бойынша есептеу және сигналдың графигін салу.
(N) есеп санын анықтаймыз, ол үшін сигнал ұзындығын (tс) дискреттеу интервалына (∆t) бөлеміз.
Котельников есептеуі бойынша t1=k∆ t ,уақыт моментін табамыз t1, мұндағы “k” 0 ден N ға дейін өзгереді(яғни 0 ден 48ге дейін өзгереді ).Осы және кейінгі есептеу нәтижелерін кестеге енгіземіз.
| Есептеу нөмері(К) | Есептік уақыт моменті t1=k∆ t | Аралық есептеу кезеңдері |
Сигнал | ||
| Мәні сos (π/2) t1 | Шамасы 1... сos(π/2) t1 | Көбейткіш e-0,6 t1 | |||
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 1 2 3 4 5 6 7 8 9 10 11 12 13 | 0 0,31 0,62 0,93 1,24 1,55 1,86 2,17 2,48 2,79 3,11 3,41 3,72 4,03 | 1 0,9 0,6 0,1 -0,4 -0,7 -0,9 -0,96 -0,73 -0,32 0,15 -0,5 0,9 0,99 | 0 0,1 0,4 0,9 1,4 1,7 1,9 1,9 1,7 1,3 0,87 1,5 0,1 0,01 | 1 0,83 0,69 0,57 0,48 0,39 0,33 0,27 0,23 0,19 0,16 0,13 0,11 0,09 | 0 0,083 0,276 0,513 0,67 0,66 0,62 0,513 0,391 0,24 0,139 0,195 0,01 0,0009 |
Кесте №1
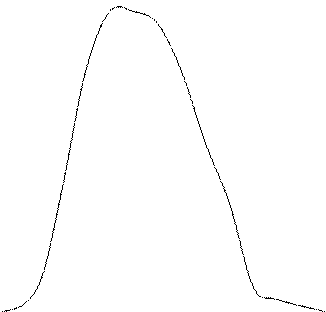
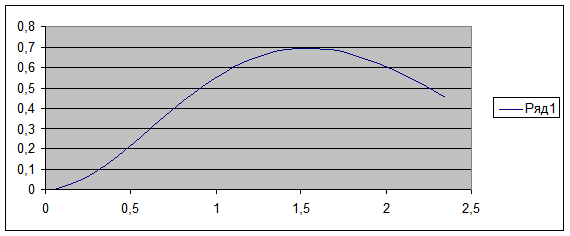
UH (t1) мәнін алған соң , UH (t) берілген сигналдың графигін тұрғызамыз.

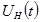
 |  |  |  |  |  |  |  |  |  |  |  |  |

 0,7
0,7

 0,6
0,6

 0,5
0,5

 0,4
0,4
 | |||||||||||||||||||||||||||
 |  |  |  |  |  |  |  |  |  |  |  |  | |||||||||||||||

 0,3
0,3
 |

















 0,2
0,2
0,1 0 0,3 0,6 0,9 1,2 1,5 1,8 2,1 2,4 2,7 3,1 3,4 3,7 4,0 
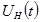 дискретизация әсерінен пайда болған
дискретизация әсерінен пайда болған 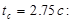 уақыт моментіндегі берілген сигналдың жаңғыруының қателігін есептеу.
уақыт моментіндегі берілген сигналдың жаңғыруының қателігін есептеу.
Берілген қателікті мына формула бойынша анықтаймыз
Мына нүктедегі сигналдың шын мәнін табамыз 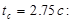
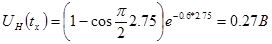
Сигналдың көрсетілген нүктедегі жуықталған мәні В.А. Котельников бойынша анықталады:
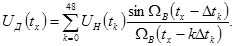
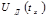 бойынша есептеуді мына кестеге 2 енгіземіз
бойынша есептеуді мына кестеге 2 енгіземіз 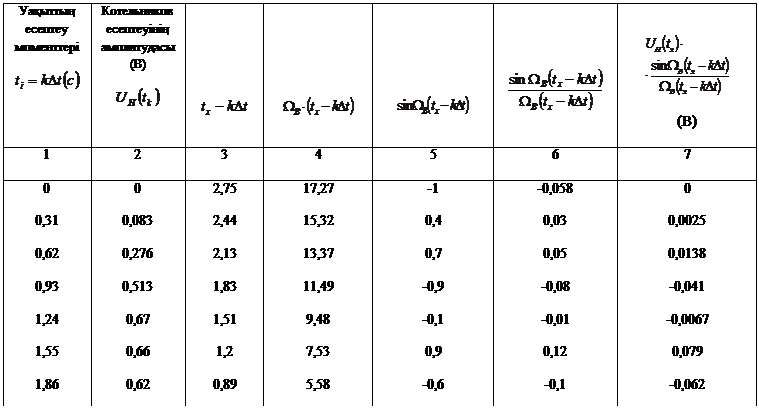
Кестенің оң жақ бағанындағы компоненттер суммасы, бұл жағдайда Котельников қатарын құрайды: 
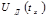 =0,2708 .
=0,2708 .
Сонда ізделген қателік:

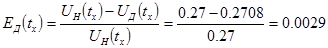 В, немесе процентпен – 29%. Қателік практикада жіберілуге болады.
В, немесе процентпен – 29%. Қателік практикада жіберілуге болады.
Есептің шығарылу жолы
fb =7
a=0,9
tc =13
tx =8
Δt=1/2 fb =1/2*7=1/14=0,071
N= tc /Δt=13/0,071=183,09
| k | ti =kΔt | Cos π/2* ti | 1- Cos π/2* ti | e-0,6 ti | UH (ti )=( 1- Cos π/2* ti ) e-0,6 ti |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0,071 | 0,993794 | 0,006206 | 0,958295 | 0,005948 |
| 2 | 0,142 | 0,975252 | 0,024748 | 0,918329 | 0,022727 |
| 3 | 0,213 | 0,944604 | 0,055396 | 0,880029 | 0,04875 |
| 4 | 0,284 | 0,902232 | 0,097768 | 0,843327 | 0,082451 |
| 5 | 0,355 | 0,84866 | 0,15134 | 0,808156 | 0,122307 |
| 6 | 0,426 | 0,784554 | 0,215446 | 0,774452 | 0,166853 |
| 7 | 0,497 | 0,71071 | 0,28929 | 0,742153 | 0,214698 |
| 8 | 0,568 | 0,628043 | 0,371957 | 0,711201 | 0,264536 |
| 9 | 0,639 | 0,537582 | 0,462418 | 0,68154 | 0,315157 |
| 10 | 0,71 | 0,440447 | 0,559553 | 0,653116 | 0,365453 |
| 11 | 0,781 | 0,337845 | 0,662155 | 0,625878 | 0,414428 |
| 12 | 0,852 | 0,23105 | 0,76895 | 0,599775 | 0,461198 |
| 13 | 0,923 | 0,121386 | 0,878614 | 0,574762 | 0,504993 |
| 14 | 0,994 | 0,010216 | 0,989784 | 0,550791 | 0,545164 |
| 15 | 1,065 | -0,10108 | 1,101081 | 0,52782 | 0,581172 |
| 16 | 1,136 | -0,21112 | 1,211123 | 0,505807 | 0,612595 |
| 17 | 1,207 | -0,31854 | 1,318545 | 0,484712 | 0,639115 |
| 18 | 1,278 | -0,42201 | 1,422012 | 0,464497 | 0,660521 |
| 19 | 1,349 | -0,52024 | 1,520241 | 0,445125 | 0,676698 |
| 20 | 1,42 | -0,61201 | 1,612013 | 0,426561 | 0,687622 |
| 21 | 1,491 | -0,69619 | 1,696188 | 0,408771 | 0,693353 |
| 22 | 1,562 | -0,77172 | 1,771722 | 0,391723 | 0,694024 |
| 23 | 1,633 | -0,83768 | 1,837676 | 0,375386 | 0,689838 |
| 24 | 1,704 | -0,89323 | 1,893232 | 0,359731 | 0,681053 |
| 25 | 1,775 | -0,9377 | 1,937701 | 0,344728 | 0,66798 |
| 26 | 1,846 | -0,97053 | 1,970531 | 0,330351 | 0,650967 |
| 27 | 1,917 | -0,99131 | 1,991313 | 0,316573 | 0,630397 |
| 28 | 1,988 | -0,99979 | 1,999791 | 0,303371 | 0,606678 |
| 29 | 2,059 | -0,99586 | 1,995859 | 0,290718 | 0,580233 |
| 30 | 2,13 | -0,97957 | 1,979565 | 0,278594 | 0,551495 |
| 31 | 2,201 | -0,95111 | 1,951113 | 0,266975 | 0,520898 |
| 32 | 2,272 | -0,91085 | 1,910854 | 0,255841 | 0,488874 |
| 33 | 2,343 | -0,85929 | 1,85929 | 0,245171 | 0,455844 |
|
|
|
|
|
|
|
|
| 0 | 0 | 8 | 50,24 | 0,9753 | 0,0194 | 0 |
| 0,071 | 0,071 | 7,929 | 49,794 | -0,993 | -0,02 | -0,0014 |
| 0,142 | 0,284 | 7,858 | 49,348 | 0,896 | 0,0182 | 0,0052 |
| 0,213 | 0,639 | 7,787 | 48,902 | -0,696 | -0,014 | -0,0091 |
| 0,284 | 1,136 | 7,716 | 48,456 | 0,4149 | 0,0086 | 0,0097 |
| 0,355 | 1,775 | 7,645 | 48,011 | -0,086 | -0,002 | -0,0032 |
| 0,426 | 2,556 | 7,574 | 47,565 | -0,252 | -0,005 | -0,0136 |
| 0,497 | 3,479 | 7,503 | 47,119 | 0,5618 | 0,0119 | 0,0415 |
| 39,831 | 15,985 | -31,831 | -199,898 | 0,3403 | -0,0017 | -0,0271 |
UH (tx)=( 1- Cos π/2* tc ) e-0,6 tc =(1-3,14/2*13)*2,7-7,8 =0,6513*0,0004= 0,0002 B
Uд (tx)=∑ UH (tx)* sin ΩB (tx –kΔt) / ΩB (tx –kΔt)= - 0,0271 B
Eд (tx) = UH (tx) - Uд (tx) / UH (tx) = (0,0002 –(-0,0271)) / (-0,0271) = 0,1007 B немесе 10 %