Рисунок 9.4 - Схема расположения сил ири движении лотка вниз
На рис. 9.4 показано направление сил, действующих на деталь при движении лотка вниз, т.е. в момент притяжения якоря электромагнита.
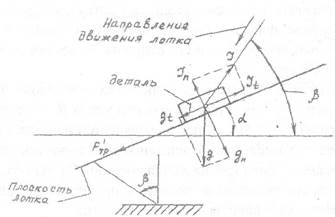
Рисунок 9.5 - Схема расположения сил при движении лотка вверх
На рис. 9.5 показано направление сил, действующих на деталь при движении лотка вверх, т.е. в момент отхода якоря от статора электромагнита.
При движении лотка вниз сила инерции, действующая на деталь, стремится сдвинуть её вдоль плоскости лотка в сторону, противоположную движению лотка.
Согласно схеме рис 9.4., имеем
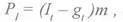(9.1)
где Р] - сила инерции, действующая на деталь в плоскости лотка;
/, - проекция ускорения лотка на его плоскость;
gl - проекция ускорения силы тяжести на плоскость лотка;
т - масса детали.
Сила трения Frp, препятствующая смещению детали относительно плоскости лотка, равна:
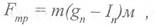(9.2)
где gm , 1т - проекции ускорения силы тяжести и лотка на вертикаль к плоскости тела;
/л - коэффициент трения между деталью и плоскостью лотка.
При движении лотка вверх имеем (согласно рис. 9.5):
Если сила инерции детали будет больше силы трения, т.е. в этом случае будет соблюдаться неравенство.
Учитывая, что при колебании лотка вверх и вниз значение углов а и b остаются постоянными, то можно считать, что абсолютные значения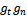 
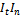также остаются постоянными.
Если сравнить силы инерции Р( и Р2 по формулам (9.1) и (9.3), то вследствие незначительной величины gt (т.к. угол а берётся в пределах 1...30), можно считать, что они равны друг другу, т.е. Р1 =Р2.
Сравнивая силы трения F 1пр и F 2пр устанавливаем, что их значения зависят от величины In согласно (9.2) и (9.4), сила трения при движении лотка уменьшается, а при движении лотка вверх - увеличивается. Таким образом, в зависимости от величины инерции лотка У, деталь на поверхности лотка будет проскальзывать на большую величину при движении лотка вниз, когда сила трения меньше, и будет проскальзывать на меньшую величину (или даже не будет проскальзывать) при движении лотка вверх, тогда сила трения детали о лоток имеет большую величину.
Величина Уп=0, если b= а, следовательно, движение детали по лотку при наличии одинакового ускорения лотка в обоих направлениях может быть обеспечено только при условия b > а.
В зависимости от величины ускорения па вертикали Iп деталь по лотку может передвигаться с проскальзыванием или подбрасыванием.
1. Если составляющая ускорения лотка Iп меньше составляющей ускорения свободного падения тела gn, то деталь не будет отделяться от лотка, и ее перемещение в плоскости лотка будет зависеть от соотношения сил трения и инерции. Следовательно, при In < gn и
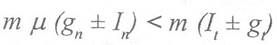
имеем движение детали с проскальзыванием.
Если составляющая ускорения лотка 1п больше, чем составляющая ускорения свободного падения тела Gn, то деталь отделится от лотка и встретится с ним тогда, когда лоток будет двигаться вверх. В этом случае произойдёт удар детали о лоток и деталь под действием сообщённой ей некоторой кинетической энергии переместится в направлении удара по некоторой траектории. Произойдет микрополет детали. Чем больше разность In — gn, тем сильнее удар и больше путь, пройденный заготовкой за один цикл.
Следовательно, при ln-gn>0 имеем движение заготовки в режиме с подбрасыванием.
Время tk, за которое лоток перемещается из одного крайнего положения в другое, есть величина постоянная и при частоте колебании 50 Гц составит 0,005 сек.
Если составляющая ускорения лотка 1п будет равна составляющей ускорения свободно падающего тела gn, то вертикальное перемещение лотка (см. рис. 9.6) можно подсчитать по формуле:
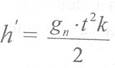
Учитывая для определенной частоты постоянство значения tk, согласно (9.5) величина вертикального перемещения лотка h будет прямо пропорциональна величине 1п
Замеряя значения h лотка работавшего вибрационного питателя, можно определить, в каком режиме он работает.
Таким образом, если h < h ' то In < gn и, следовательно, вибробункер будет работать в режиме с проскальзыванием.
Если же h > h ' , то Уn. > gn и вибробункер будет работать в режиме с подбрасыванием.
Определение производительности ВБЗУ
Если известна скорость перемещения детали по лотку вибробункера, то производительность вибробункера Q можно подсчитать по следующей формуле:
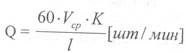
где V - средняя скорость перемещения детали по лотку вибробункера, мм/с;
/ - размер заготовки в направлении движения, мм;
К - коэффициент заполнения, учитывающий разрывы в потоке заготовок, движущихся по лотку, принимается равным 0,40-0,55.
Теоретически средняя скорость передвижения деталей по лотку можно определить исходя из следующих рассуждений.
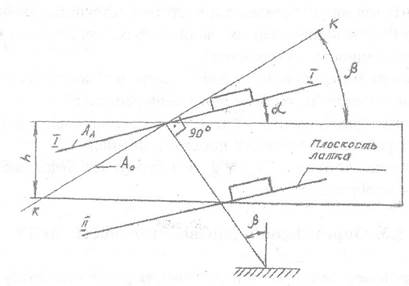
Направление колебаний лотка! обычно принимается как совпадавшее с направлением прямой К-К (см. рис. 9.6), перпендикулярной пружинам, что при большом значении соотношения между длиной пружин и амплитудой колебаний лотка практически полностью соответствует действительности. Направление действия возмущающих усилий вибратора, будут ли они совпадать с направлением прямой К-К или осью бункера, принципиального значения не имеет. Полагая, что лоток совершает в направлении прямой К-К гармонические колебания с круговой частотой w и амплитудой Ао и мгновенное положение его в момент времени t описывается уравнением:
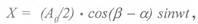
то скорость лотка выражается через производную перемещения:
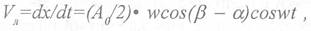
гдеА0 - размах колебаний лотка в направлении, перпендикулярном рессорам;
м>=2Пц - круговая частота колебаний; ц - частота колебаний, ц =50 Гц
b - угол наклона рессора или угол наклона колебания, b - 30°; a - угол наклона плоскости лотка, а = 2°.
Если обозначить размах колебаний лотка в направлении его плоскости через Ал, то скорость лотка:
V л= (А0/2)* cos wt , (9.9)
где Ал – А0 cos ( b - а).
Подставляя в формулу (9.9) значение w, получаем другое выражение значения скорости лотка вибробункера
Ve = Ал Пц cos wt. (9.10)
Отсюда максимальная скорость лотка будет
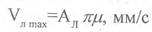
С учетом режима работы вибробункера, среднюю скорость движения деталей по лотку можно выразить следующей формулой
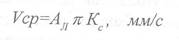
где К - коэффициент скорости, показывающий, насколько средняя скорость заготовки в данном режиме приближается к максимальной скорости лотка.
Для режима с проскальзыванием Кс =1,02 + 1,06
Для режима с подбрасыванием Кс =1,88 + 1.92.