1. Сметана имеет жирность (Рис. 2). Как это сказать по-другому?
Тема урока : Проценты на 09.04
На этом уроке мы узнаем, что такое проценты, где они встречаются и как с ними работать. Решим несколько примеров на вычисление процентов.
Если у вас возникнет сложность в понимании тему, рекомендуем посмотреть урок «Десятичные дроби и проценты».
Введение
Прочитаем на латыни 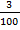 . Это будет звучать как «
. Это будет звучать как « 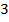 pro centum –
pro centum – 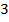 на сотню». Или в -русском варианте «
на сотню». Или в -русском варианте « 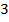 процента». То есть процент – это название «сотая» по-латыни. Кроме названия, есть и свой символ
процента». То есть процент – это название «сотая» по-латыни. Кроме названия, есть и свой символ 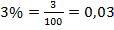 .
.
Зачем нужны проценты? В математике не нужны. Здесь уже есть десятичные дроби, в том числе сотые. Проценты – это договоренность, чтобы лучше понимать друг друга, в таких науках, как экономика, статистика, социология и т.д.
Задача
В одном классе учится 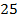 человек, из них
человек, из них 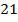 хорошист, в другом
хорошист, в другом 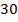 человек, из них
человек, из них 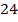 хорошиста (Рис. 1). Где успеваемость выше?
хорошиста (Рис. 1). Где успеваемость выше?
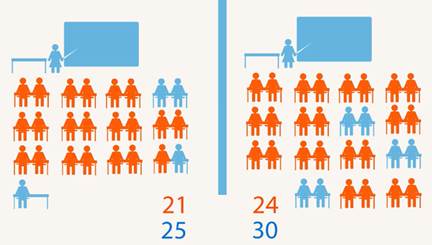
Рис. 1. Иллюстрация к условию задачи
Решение
В одном классе хорошисты составляют 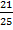 часть, а во втором –
часть, а во втором – 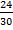 части. Где этот показатель выше, то есть какая из этих дробей больше? Чтобы понять, нужно привести дроби к одному знаменателю и сравнить. Во многих профессиях (экономика, финансы) договорились такие показатели сразу считать со знаменателем
части. Где этот показатель выше, то есть какая из этих дробей больше? Чтобы понять, нужно привести дроби к одному знаменателю и сравнить. Во многих профессиях (экономика, финансы) договорились такие показатели сразу считать со знаменателем 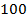 .
.
Приведем наши дроби к знаменателю 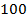 :
:
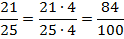
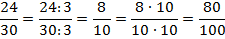
Теперь все просто: 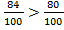 .
.
Но это и есть проценты: 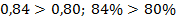 .
.
Ответ: в первом классе хорошистов больше, чем во втором.
Эквивалентные записи
Итак, в математике 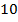 -е,
-е, 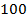 -е,
-е, 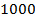 -е. В финансах, экономике – проценты. Потренируемся переходить от одной эквивалентной записи к другой и наоборот.
-е. В финансах, экономике – проценты. Потренируемся переходить от одной эквивалентной записи к другой и наоборот.
1. Сметана имеет жирность 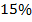 (Рис. 2). Как это сказать по-другому?
(Рис. 2). Как это сказать по-другому?

Рис. 2. Сметана
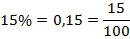
2. 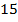 минут – это четверть часа (Рис. 3). Как то же самое сказать с использованием процентов?
минут – это четверть часа (Рис. 3). Как то же самое сказать с использованием процентов?

Рис. 3. Четверть часа
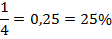
3. В этом году выпало  осадков от нормы (Рис. 4). Как это можно сказать по-другому?
осадков от нормы (Рис. 4). Как это можно сказать по-другому?
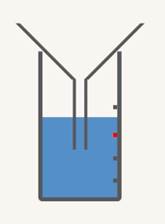
Рис. 4. Количество осадков выше нормы
Ну, во-первых,  – это на
– это на 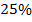 больше, чем
больше, чем 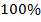 . То есть можно сказать «выпало на
. То есть можно сказать «выпало на 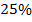 больше обычного».
больше обычного».
Если перевести в десятичную дробь, то можно сказать, что в этом году осадки составили 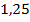 от нормы (или на
от нормы (или на 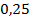 больше обычного).
больше обычного).
Переход от процентов к десятичной дроби
Десятичные дроби – удобный математический инструмент для расчетов. Если нужно решить задачу на проценты, то лучше всегда переходить от процентов к записи в виде десятичной дроби.
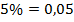
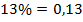
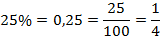
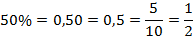
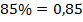
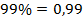
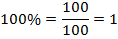
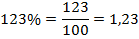
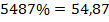
Может случиться, что самих процентов окажется дробное количество. Никакого значения для нас это не имеет.
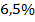 (шесть с половиной процентов). Уменьшаем в
(шесть с половиной процентов). Уменьшаем в 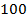 раз, т.е. переносим десятичную запятую влево на две позиции:
раз, т.е. переносим десятичную запятую влево на две позиции: 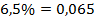 .
.
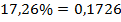
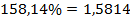
Итак, чтобы перевести проценты в десятичную дробь, нужно количество процентов уменьшить в 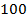 раз, сдвинуть запятую влево на
раз, сдвинуть запятую влево на 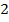 позиции.
позиции.
Переход от десятичной дроби к процентам
В задачах на проценты часто и ответ надо дать в процентах. Потренируемся делать переход в обратную сторону, десятичную дробь записывать в процентах.
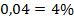
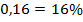
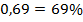
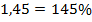
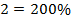
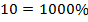
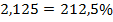
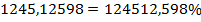
Итак:
· чтобы перейти от процентов к десятичной дроби, нужно число уменьшить в 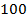 раз, перенести запятую влево на две позиции;
раз, перенести запятую влево на две позиции;
· чтобы совершить обратный переход от десятичной дроби к процентам, надо увеличить число в 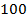 раз, перенести запятую вправо на две позиции.
раз, перенести запятую вправо на две позиции.
Промежуточный итог
Давайте подведем итог.
· Мы разобрались, что такое процент. Это международное название для одной сотой.
· Мы научились переходить от одной эквивалентной записи к другой. От процентов, которые используются во многих науках к десятичным дробям (т.е. уже к математическому инструменту), и обратно.
Нахождение процента от числа
Пример 1
Найти 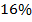 от
от 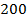 .
.
Решение
Так как 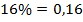 , то теперь задача для нас звучит так – «найти
, то теперь задача для нас звучит так – «найти 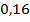 от
от  ».
».
Но, чтобы найти дробь от числа, нужно число умножить на эту дробь: 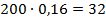 .
.
Итак, 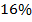 от
от 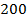 это
это 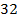 .
.
Ответ: 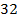 .
.
Пример 2
От 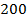 найти
найти 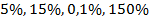 .
.
Решение
1. 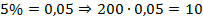 .
.
2. 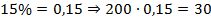 .
.
3. 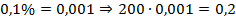 .
.
4. 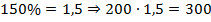 .
.
Заключение
На следующем уроке мы подробно рассмотрим, какие виды задач на проценты обычно встречаются, и научимся их решать. Рассмотрим общий алгоритм решения любой задачи на проценты.
Домашнее задание
1. Переведите десятичную дробь в проценты: а) 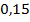 ; б)
; б) 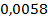 ; в)
; в) 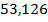 ;
; 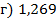 .
.
2. Переведите проценты в десятичную дробь: а) 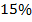 ; б)
; б) 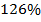 ; в)
; в) 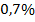 ; г)
; г) 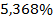 .
.
3. Найдите процент от величины:
а) 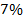 от
от 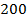 м
м
б) 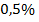 от
от 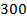 г
г
в) 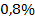 от
от 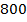 кг
кг
г) 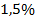 от
от 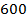 дм
дм
Десятичные дроби и проценты
П 37 стр. 252 № 1063,1065,1068,1072,1074,1075








