§ 2. Об однородных расширениях частичных геометрий.
Геометрия  ранга 2 – это система инцидентности
ранга 2 – это система инцидентности 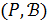 , где
, где 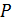 – множество точек,
– множество точек, 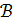 – некоторый набор подмножеств
– некоторый набор подмножеств 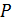 , называемых блоками. Два блока называются коллинеарными, если они лежат в общем блоке. Если
, называемых блоками. Два блока называются коллинеарными, если они лежат в общем блоке. Если  является геометрией ранга 2, то точечный граф
является геометрией ранга 2, то точечный граф 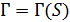 – это граф с множеством вершин
– это граф с множеством вершин 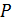 , в котором различные вершины смежны, если они коллинеарны. Геометрия
, в котором различные вершины смежны, если они коллинеарны. Геометрия  будет называться связной, регулярной и т.д., если граф
будет называться связной, регулярной и т.д., если граф 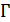 обладает соответствующими свойствами.
обладает соответствующими свойствами.
Пара 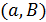 , из
, из 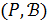 , называется флагом, если точка
, называется флагом, если точка 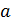 принадлежит блоку
принадлежит блоку 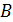 , и антифлагом в противном случае. Если
, и антифлагом в противном случае. Если 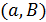 является антифлагом, то через
является антифлагом, то через 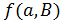 обозначим число точек в
обозначим число точек в 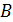 , коллинеарных
, коллинеарных 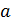 . Геометрия называется
. Геометрия называется 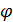 – однородной (
– однородной ( 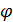 – натуральное число), если для любого антифлага
– натуральное число), если для любого антифлага 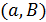 число
число 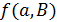 равно 0 или
равно 0 или 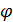 , и сильно
, и сильно 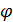 - однородной, если это число всегда равно
- однородной, если это число всегда равно 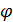 .
.
Вычет 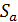 геометрии
геометрии  в точке
в точке 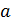 – это геометрия
– это геометрия 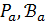 ранга 2, где
ранга 2, где 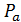 – множество всех точек, коллинеарных
– множество всех точек, коллинеарных 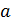 , и
, и 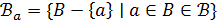 . Пусть
. Пусть 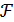 - семейство геометрий ранга 2, и всякий вычет
- семейство геометрий ранга 2, и всякий вычет 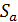 лежит в
лежит в 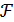 . Тогда говорят, что S является расширением
. Тогда говорят, что S является расширением 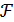 . Геометрия
. Геометрия  называется треугольной, если для любых попарно коллинеарных точек
называется треугольной, если для любых попарно коллинеарных точек 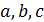 найдется блок, содержащий все три точки
найдется блок, содержащий все три точки 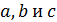 . Точечный граф
. Точечный граф 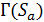 - это подграф (возможно, собственный) графа, индуцированного на
- это подграф (возможно, собственный) графа, индуцированного на 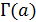 графом
графом 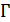 . Заметим, что
. Заметим, что 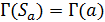 для любой точки
для любой точки 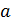 тогда и только тогда, когда геометрия
тогда и только тогда, когда геометрия  треугольная.
треугольная.
Если 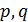 - различные точки геометрии
- различные точки геометрии  , то геометрия
, то геометрия 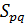 имеет множество точек
имеет множество точек 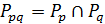 и множество блоков
и множество блоков 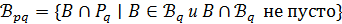 . Положим
. Положим 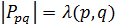 (соответственно,
(соответственно, 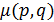 ), если
), если 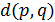 равно 1 (соответственно, 2) в точечном графе
равно 1 (соответственно, 2) в точечном графе 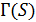 .
.
Блоки геометрии  называются прямыми, если различные блоки пересекаются не более чем в одной точке. В этом случае множество блоков называется множеством прямых и мы будем пользоваться неформальным языком, т.е. такими выражениями, как “прямая проходит через точку”, “точка лежит на прямой” и др.
называются прямыми, если различные блоки пересекаются не более чем в одной точке. В этом случае множество блоков называется множеством прямых и мы будем пользоваться неформальным языком, т.е. такими выражениями, как “прямая проходит через точку”, “точка лежит на прямой” и др.
Если  есть такая геометрия точек и прямых, что каждая прямая имеет ровно
есть такая геометрия точек и прямых, что каждая прямая имеет ровно 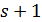 точку, каждая точка лежит ровно на
точку, каждая точка лежит ровно на 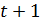 прямой
прямой 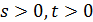 и
и  является сильно -однородной
является сильно -однородной 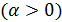 то тогда
то тогда  называется
называется 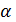 - частичной геометрией порядка
- частичной геометрией порядка 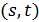 (для краткости
(для краткости 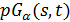 или даже
или даже 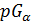 ). Связное расширение семейства частичных геометрий
). Связное расширение семейства частичных геометрий 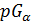 обозначается как
обозначается как 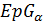 (или даже
(или даже 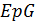 ).
).
Можно показать, что в 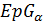 - геометрии
- геометрии 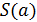 для любого антифлага
для любого антифлага 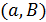 , если
, если 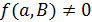 , то
, то 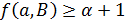 и
и 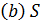 является треугольной геометрией тогда и только тогда, когда она
является треугольной геометрией тогда и только тогда, когда она 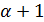 - однородна.
- однородна.
Если  - частичная геометрия
- частичная геометрия 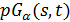 , то двойственная геометрия
, то двойственная геометрия 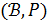 , в которой каждая точка отождествляется с пучком проходящих через нее прямых, является частичной геометрией
, в которой каждая точка отождествляется с пучком проходящих через нее прямых, является частичной геометрией 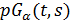 . Обобщенный четырехугольник
. Обобщенный четырехугольник 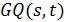 - это частичная геометрия
- это частичная геометрия 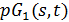 . Геометрия
. Геометрия 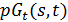 является сетью, а
является сетью, а 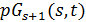 является 2-схемой с
является 2-схемой с 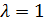 . Коклика из
. Коклика из 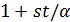 точек в точечном графе геометрии
точек в точечном графе геометрии 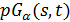 называется овоидом.
называется овоидом.
В данной работе мы исследуем 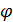 – однородные геометрии
– однородные геометрии 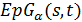 с
с 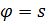 и сильно
и сильно 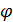 – однородные геометрии с
– однородные геометрии с 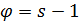 .
.
Пусть геометрия  является
является 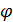 – однородной
– однородной 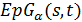 . Если
. Если 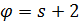 то
то  называется одноточечным расширением (и граф
называется одноточечным расширением (и граф 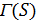 является полным). Например, 3-схема Матье с параметрами
является полным). Например, 3-схема Матье с параметрами 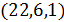 - это одноточечное расширение проективной плоскости
- это одноточечное расширение проективной плоскости 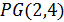 .
.
Если 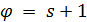 , то геометрия
, то геометрия  будет сильно (
будет сильно ( 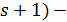 однородной, и
однородной, и 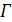 является полным многодольным графом
является полным многодольным графом 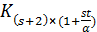 . В этом случае для любой точки a множество точек вычета
. В этом случае для любой точки a множество точек вычета 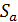 имеет разбиение на
имеет разбиение на 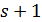 овоидов. Среди известных обобщенных четырехугольников только
овоидов. Среди известных обобщенных четырехугольников только 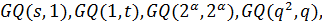
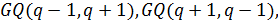 где
где 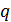 – степень простого числа, допускают разбиение точечного множества на овоиды.
– степень простого числа, допускают разбиение точечного множества на овоиды.
Пример 1. Для любого 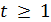 имеется единственная геометрия
имеется единственная геометрия 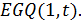 Ее точечный граф является полным трехдольным графом
Ее точечный граф является полным трехдольным графом 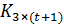 , а множество блоков совпадает с множеством 3-клик этого графа.
, а множество блоков совпадает с множеством 3-клик этого графа.
Пример 2. Сильно 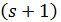 - однородный расширенный четырехугольник
- однородный расширенный четырехугольник 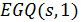 существует при всех
существует при всех 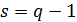 , где
, где 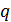 есть степень 2, а при
есть степень 2, а при 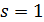 и
и 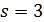 является единственным.
является единственным.
Пусть 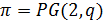 ,
, 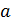 - точка в
- точка в 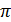 ,
, 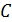 - гиперовал, содержащий
- гиперовал, содержащий 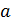 , а
, а 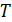 обозначает группу (порядка
обозначает группу (порядка 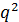 ) всех элаций с центром в точке
) всех элаций с центром в точке 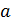 . Точками
. Точками 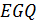 являются все точки
являются все точки 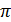 , отличные от
, отличные от 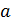 ; блоками являются прямые, не содержащие
; блоками являются прямые, не содержащие 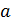 , и трансляции прямой
, и трансляции прямой 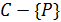 под действием группы
под действием группы 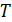 .
.
Примеры 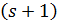 -однородных
-однородных 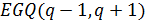 для
для 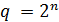 построены
построены 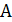 . Пасини и Д. Пасечником.
. Пасини и Д. Пасечником.
Теорема 1. Пусть S является s -однородной геометрией 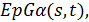 а
а 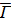 -дополнение к
-дополнение к 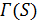 . Тогда либо
. Тогда либо 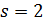 (и геометрия
(и геометрия  известна), либо
известна), либо  есть
есть 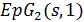 ,
, 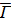 - является сильно регулярным графом с
- является сильно регулярным графом с 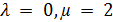 , и
, и  есть геометрия вершин и клик графа
есть геометрия вершин и клик графа 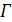 , соответствующих
, соответствующих 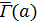 для
для 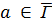 ; либо
; либо  сильно
сильно 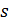 -однородна и одно из следующих утверждений верно:
-однородна и одно из следующих утверждений верно:
(1) 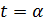 , и
, и 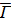 есть граф, являющийся квадратной решеткой на
есть граф, являющийся квадратной решеткой на 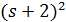 вершинах;
вершинах;
(2) 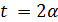 ,
, 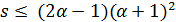 ,
, 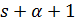 делит
делит 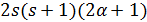 , и
, и 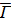 есть треугольный граф на (
есть треугольный граф на ( 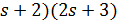 вершинах.
вершинах.
Пример 3. Сильно -однородная геометрия 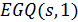 существует для всех
существует для всех 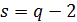 , где
, где 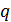 есть степень двойки.
есть степень двойки.
Пусть 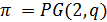 ,
, 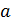 и
и 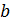 являются точками
являются точками 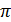 ,
, 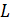 есть прямая
есть прямая 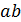 ,
, 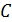 -гиперовал, содержащий
-гиперовал, содержащий 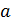 и
и 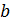 , а
, а 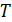 - это группа всех центральных коллинеаций с центром
- это группа всех центральных коллинеаций с центром 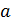 и осью, содержащей
и осью, содержащей 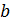 . Тогда
. Тогда 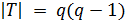 ,
, 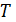 фиксирует все прямые, проходящие через
фиксирует все прямые, проходящие через 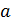 , и является точно 2-транзитивной группой на множестве прямых, проходящих через
, и является точно 2-транзитивной группой на множестве прямых, проходящих через 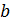 и отличных от
и отличных от 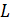 .
.
Множество точек геометрии 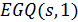 состоит из точек
состоит из точек 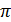 , которые не лежат на L, а множество блоков является объединением множества прямых
, которые не лежат на L, а множество блоков является объединением множества прямых 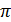 , не содержащих
, не содержащих 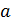 или
или 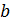 , и образов
, и образов 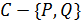 под действием группы элаций
под действием группы элаций 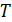 .
.
Пример 4. Сильно 3-однородная геометрия 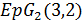 существует.
существует.
Пусть точечное множество  есть множество позиций
есть множество позиций 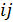 квадратной матрицы порядка 5, а множество блоков
квадратной матрицы порядка 5, а множество блоков 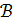 задано наборами
задано наборами 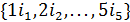 , такими, что
, такими, что 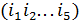 - перестановка.
- перестановка.
Ясно, что  для
для  и
и 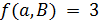 для любого антифлага
для любого антифлага 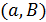 .
.
Далее, для точки 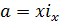 имеем
имеем 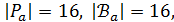 каждая точка из
каждая точка из 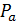 принадлежит трем блокам из
принадлежит трем блокам из 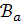 и каждый блок из
и каждый блок из 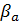 содержит 4 точки из
содержит 4 точки из 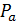 . Таким образом,
. Таким образом, 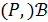 является сильно 3-однородной геометрией
является сильно 3-однородной геометрией 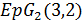 .
.
Теорема 2. Пусть  является сильно
является сильно 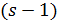 -однородной геометрией
-однородной геометрией 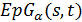 . Тогда либо
. Тогда либо  является геометрией
является геометрией 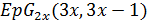 для некоторого нечетного
для некоторого нечетного 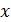 , либо
, либо  равняется
равняется 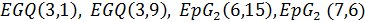 или
или 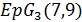 .
.
Дж. Тас построил частичную геометрию 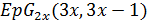 с
с 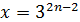 с помощью спреда гиперболической квадрики в проективном пространстве
с помощью спреда гиперболической квадрики в проективном пространстве 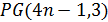 . К настоящему времени известно существование такого спреда только для случая
. К настоящему времени известно существование такого спреда только для случая 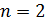 .
.
Теоремы 1 и 2 обобщают соответствующие результаты П. Камерона и Дж. Фишера по расширениям обобщенных четырехугольников на случай частичных геометрий.
1. Предварительные результаты
В этом разделе доказаны некоторые необходимые вспомогательные результаты.
Лемма 1.1. Пусть  является частичной геометрией
является частичной геометрией 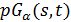 . Тогда
. Тогда 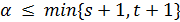 и выполняются следующие утверждения:
и выполняются следующие утверждения:
(1) точечный граф 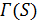 является сильно регулярным с
является сильно регулярным с 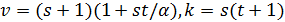 ,
,
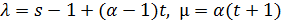 , и
, и 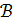 содержит
содержит 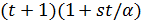 прямых;
прямых;
(2) 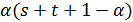 делит
делит 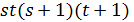 (условие целочисленности);
(условие целочисленности);
(3) (s+1−2α)t ≤(s−1)(s+1−α)2 (условие Крейна);
(4) если  содержит подгеометрию
содержит подгеометрию 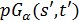 , то
, то 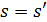 или
или 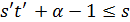 .
.
Лемма 1.2. Пусть  является -однородной геометрией
является -однородной геометрией 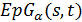 . Тогда точечный граф
. Тогда точечный граф 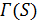 является реберно регулярным с
является реберно регулярным с 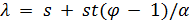 . Кроме того,
. Кроме того, 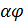 делит
делит 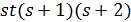 , и в случае
, и в случае 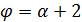 число
число 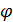 четно.
четно.
Пусть далее 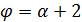 и
и 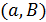 является антифлагом с
является антифлагом с 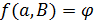 . По структуре вычета
. По структуре вычета 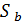 для
для 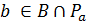 точка
точка 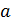 лежит на
лежит на 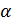 прямых в
прямых в 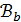 , пересекающих
, пересекающих 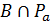 , так что
, так что 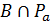 содержит единственную точку
содержит единственную точку 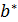 такую, что тройка
такую, что тройка 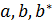 не лежит ни в одном из блоков множества
не лежит ни в одном из блоков множества 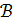 . Ясно, что
. Ясно, что 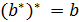 , поэтому число
, поэтому число 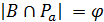 четно.
четно.
Лемма 1.3. Пусть  - сильно -однородная геометрия
- сильно -однородная геометрия 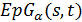 , где
, где 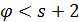 . Тогда точечный граф
. Тогда точечный граф 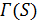 является псевдогеометрическим для
является псевдогеометрическим для 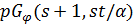 и имеет собственные значения
и имеет собственные значения 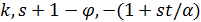 .
.
Лемма 1.4. 3-однородное расширение частичной геометрии 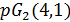 не существует.
не существует.
Доказательство. Пусть  является точечным графом 3-однородной геометрии
является точечным графом 3-однородной геометрии 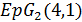 . Тогда
. Тогда  сильно регулярен с параметрами
сильно регулярен с параметрами 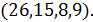 Так как эта геометрия треугольная, то подграф
Так как эта геометрия треугольная, то подграф 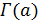 является треугольным графом T
является треугольным графом T 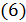 для любого
для любого 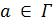 . Значит, окрестности вершин в каждом
. Значит, окрестности вершин в каждом 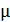 -подграфе графа
-подграфе графа 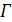 являются четырехугольниками, что противоречит равенству
являются четырехугольниками, что противоречит равенству 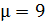 . Лемма доказана.
. Лемма доказана.
2. Случай 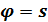
Предположим, что  есть - однородное расширение частичной геометрии порядка
есть - однородное расширение частичной геометрии порядка 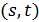 , т. е.
, т. е. 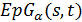 . Пусть
. Пусть 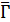 является дополнением к графу
является дополнением к графу 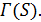
Лемма 2.1. Допустим, что геометрия  сильно -однородна. Тогда либо
сильно -однородна. Тогда либо 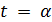 и
и 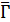 -квадратная
-квадратная 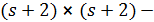 решетка, либо
решетка, либо 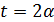 и
и 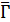 является треугольным графом
является треугольным графом 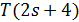 , где
, где 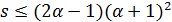 .
.
Доказательство. По лемме 1.3 граф 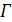 имеет собственное значение
имеет собственное значение 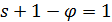 , и по теореме Зейделя граф
, и по теореме Зейделя граф 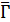 является одним из следующих графов: решетка или треугольный граф, полный многодольный граф
является одним из следующих графов: решетка или треугольный граф, полный многодольный граф 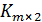 , граф Петерсена, Шрикханде, Чанга, Клебша или Шлефли. Заметим,
, граф Петерсена, Шрикханде, Чанга, Клебша или Шлефли. Заметим, 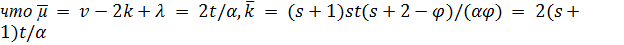 и
и
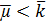 , поэтому графы
, поэтому графы 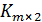 исключаются.
исключаются.
Так как граф Петерсена имеет параметры 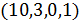 , то
, то 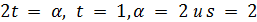 , противоречие с тем, что
, противоречие с тем, что 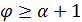 . В случае графа Клебша граф
. В случае графа Клебша граф 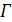 имеет параметры (
имеет параметры ( 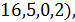 противоречие с тем, что
противоречие с тем, что 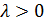 .
.
В случае графа Шлефли граф 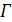 имеет параметры
имеет параметры 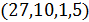 и
и 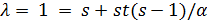 , поэтому
, поэтому 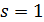 , снова противоречие с тем, что
, снова противоречие с тем, что 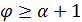 .
.
Пусть 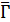 имеет параметры решетки
имеет параметры решетки 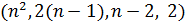 . Тогда
. Тогда 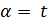 . Заметим, что граф Шрикханде имеет параметры решетки при
. Заметим, что граф Шрикханде имеет параметры решетки при 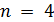 . Но существует единственное расширение обобщенного четырехугольника
. Но существует единственное расширение обобщенного четырехугольника 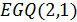 с
с 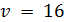 , и его точечный граф является дополнением к
, и его точечный граф является дополнением к 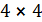 -решетке.
-решетке.
Пусть, наконец, 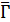 имеет параметры
имеет параметры 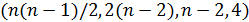 треугольного графа. Тогда
треугольного графа. Тогда 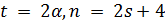 . По условию Крейна для
. По условию Крейна для 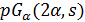 имеем
имеем 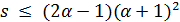 . Будем считать, что
. Будем считать, что 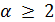 . Но тогда
. Но тогда 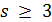 ,
, 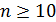 и графы Чанга
и графы Чанга 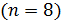 не возникают.
не возникают.
Лемма 2.2. Пусть  является -однородной геометрией
является -однородной геометрией 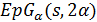 с
с 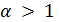 и
и 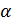 делит
делит 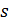 . Тогда
. Тогда 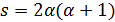 .
.
Доказательство. Положим 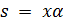 . В случае
. В случае 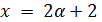 имеем
имеем 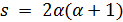 , и заключение леммы выполняется.
, и заключение леммы выполняется.
По лемме 1.1 число 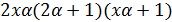 делится на
делится на 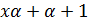 . Далее, числа
. Далее, числа 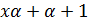 и
и 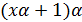 взаимно просты, поэтому
взаимно просты, поэтому 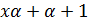 делит
делит 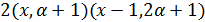 . Наконец,
. Наконец, 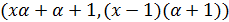 делит
делит 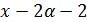 и
и 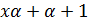 делит
делит 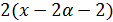 .
.
Пусть 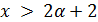 . Тогда
. Тогда 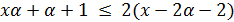 и
и 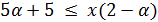 , так что
, так что 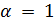 , противоречие. Если
, противоречие. Если 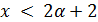 , то
, то 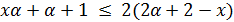 , поэтому
, поэтому 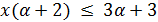 и
и 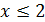 .
.
Поскольку 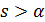 , то
, то 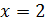 и по условию целочисленности для
и по условию целочисленности для 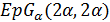 число
число 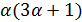 делит
делит 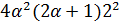 . Значит,
. Значит, 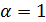 , что противоречит условию леммы.
, что противоречит условию леммы.
Лемма 2.3. Пусть  является -однородной геометрией. Тогда либо
является -однородной геометрией. Тогда либо 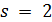 , либо
, либо 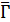 является сильно регулярным графом с
является сильно регулярным графом с 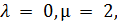 и
и  - геометрия вершин и клик графа
- геометрия вершин и клик графа 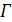 , соответствующих
, соответствующих 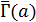 для
для 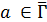 , либо
, либо 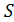 сильно однородна.
сильно однородна.
Доказательство. Допустим, что  - контрпример к этой лемме с минимально возможным
- контрпример к этой лемме с минимально возможным 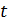 . Имеем
. Имеем 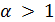 , так что
, так что 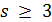 . Диаметр графа
. Диаметр графа 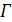 ограничен величиной
ограничен величиной 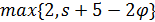 , значит,
, значит, 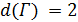 .
.
По выбору  в ней найдутся точки
в ней найдутся точки 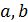 на расстоянии 2 такие, что
на расстоянии 2 такие, что 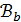 содержит блоки двух типов: блоки
содержит блоки двух типов: блоки 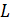 с
с 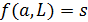 (
( 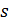 -блоки) и блоки
-блоки) и блоки 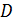 с
с 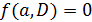 (
( 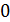 -блоки).
-блоки).
Пусть 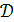 есть геометрия с точечным множеством
есть геометрия с точечным множеством 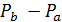 и множеством блоков
и множеством блоков 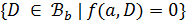 . Тогда каждый блок из
. Тогда каждый блок из 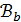 , содержащий две точки
, содержащий две точки 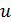 и
и 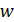 множества
множества 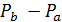 , является
, является 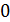 -блоком. Таким образом, геометрия
-блоком. Таким образом, геометрия 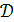 сильно -однородна. Следовательно, либо
сильно -однородна. Следовательно, либо 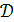 есть геометрия точек единственного
есть геометрия точек единственного 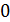 -блока, либо
-блока, либо 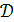 есть геометрия
есть геометрия 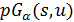 для некоторого
для некоторого 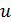 .
.
В первом случае число точек в 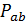 равно
равно 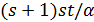 . Далее, каждый блок множества
. Далее, каждый блок множества 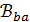 , содержащий точку из
, содержащий точку из 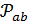 , содержит единственную точку из
, содержит единственную точку из 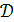 , поскольку
, поскольку 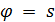 . Так что число ребер между точками множеств
. Так что число ребер между точками множеств  и
и  равно
равно 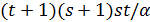 . Однако каждая точка геометрии
. Однако каждая точка геометрии 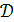 лежит в
лежит в 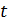 блоках из
блоках из 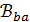 , содержащих по s точек множества
, содержащих по s точек множества 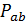 , поэтому то же число ребер равно
, поэтому то же число ребер равно 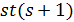 . Значит,
. Значит, 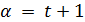 (и этот случай не возникает в расширенном четырехугольнике
(и этот случай не возникает в расширенном четырехугольнике 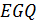 ).
).
В случае 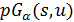 имеется
имеется 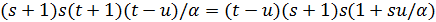 ребер между точками геометрии
ребер между точками геометрии 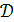 и
и 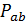 , поэтому
, поэтому 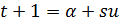 .
.
Допустим, что выполняется первый случай. Тогда 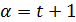 . Пусть для
. Пусть для 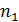 точек
точек 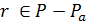 каждый блок множества
каждый блок множества 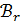 является -блоком, и для
является -блоком, и для 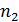 точек
точек 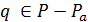 все точки множества
все точки множества 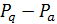 лежат в единственном
лежат в единственном 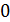 -блоке. Тогда число ребер между точками множеств
-блоке. Тогда число ребер между точками множеств 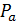 и
и 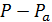 равно
равно
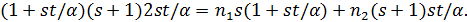
Если 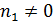 , то по целочисленности числа точек в множествах
, то по целочисленности числа точек в множествах 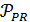 и
и 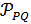 число
число 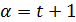 делит
делит 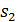 и
и 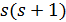 , поэтому
, поэтому 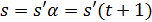 . Далее,
. Далее, 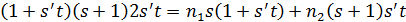 и
и  делит
делит 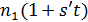 . Так как
. Так как 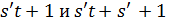 взаимно просты, то
взаимно просты, то 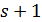 делит
делит 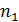 . Если
. Если 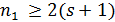 , то
, то 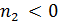 , если же
, если же 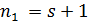 , то
, то 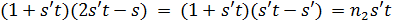 и
и 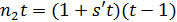 . Поэтому
. Поэтому 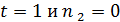 , противоречие.
, противоречие.
Итак, 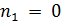 , граф
, граф  разбивается на
разбивается на 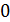 -блоки и
-блоки и 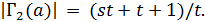 Значит,
Значит, 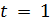 ,
, 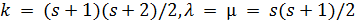 , поэтому граф
, поэтому граф 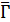 сильно регулярен с
сильно регулярен с 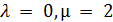 , и
, и  является геометрией вершин и клик графа
является геометрией вершин и клик графа 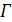 , соответствующих
, соответствующих 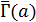 для
для 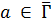 . Но это противоречит выбору
. Но это противоречит выбору  .
.
Таким образом, мы доказали, что для любой точки 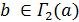
(1) каждый блок из 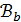 является -блоком или
является -блоком или
(2) 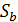 содержит подгеометрию
содержит подгеометрию 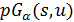 с точечным множеством
с точечным множеством 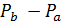 и множеством блоков
и множеством блоков 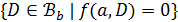 , причем
, причем 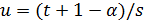 .
.
Пусть 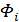 - множество точек графа
- множество точек графа 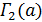 , удовлетворяющее утверждению
, удовлетворяющее утверждению 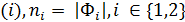 . Заметим, что если
. Заметим, что если 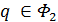 и точка
и точка 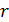 лежит в
лежит в 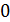 -блоке
-блоке 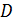 из
из 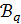 , то
, то 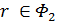 . Следовательно,
. Следовательно, 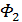 разбивается на
разбивается на 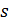 -однородные подгеометрии
-однородные подгеометрии 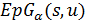 . По индукции мы заключаем, что либо
. По индукции мы заключаем, что либо 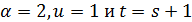 , либо эти подгеометрии сильно однородны, и по лемме 2.1 имеем
, либо эти подгеометрии сильно однородны, и по лемме 2.1 имеем 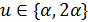 .
.
Как и выше, у нас имеется равенство для количества ребер между точками множеств 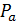 и
и 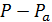 :
:
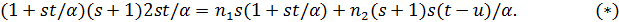
В первом случае 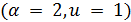 имеем
имеем 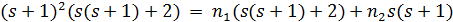 , поэтому
, поэтому 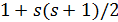 делит
делит 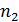 . Если
. Если 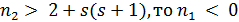 , что абсурдно. Значит,
, что абсурдно. Значит, 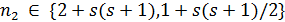 . Так как
. Так как 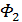 разбивается на подгеометрии
разбивается на подгеометрии 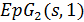 , то
, то 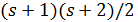 делит
делит 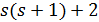 , поэтому
, поэтому 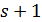 делит 4 и
делит 4 и 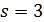 . Противоречие с тем, что
. Противоречие с тем, что 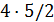 не делит
не делит 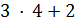 .
.
Предположим теперь, что 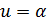 . Тогда t
. Тогда t 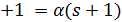 и по утверждению (2) леммы 1.1 число
и по утверждению (2) леммы 1.1 число 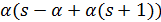 делит s
делит s 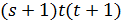 , поэтому
, поэтому 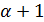 делит
делит 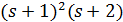 . Далее,
. Далее, 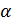 делит
делит 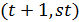 , поэтому
, поэтому 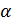 делит
делит 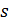 . Положим
. Положим 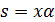 . Тогда
. Тогда 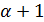 делит
делит 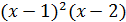 .
.
Если 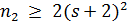 , то из равенства
, то из равенства  следует, что
следует, что 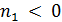 , что противоречиво. Значит,
, что противоречиво. Значит, 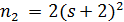 иравенство
иравенство 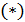 принимает вид:
принимает вид: 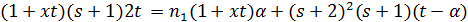 . Отсюда
. Отсюда 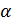 делит
делит  делит (
делит ( 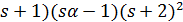 . Далее,
. Далее, 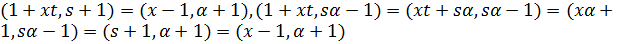 и
и 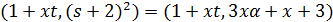 . Так как
. Так как 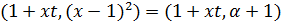 , то
, то 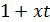 делит
делит 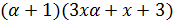 , откуда
, откуда 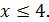
Если 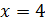 , то
, то 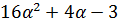 делит
делит 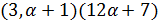 , поэтому
, поэтому 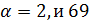 не делит
не делит 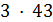 .
.
Если 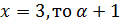 делит 4, и
делит 4, и 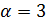 . Но тогда
. Но тогда 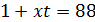 не делит
не делит 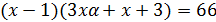 . Значит,
. Значит, 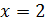 , противоречие с тем, что
, противоречие с тем, что 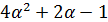 не делит
не делит 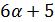 .
.
Итак, 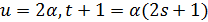 , и по лемме 1.1 число α
, и по лемме 1.1 число α 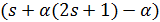 делит
делит 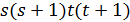 , поэтому
, поэтому 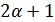 делит
делит 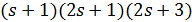 . Как и выше,
. Как и выше, 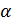 делит
делит 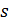 , и по лемме 2.2 имеем
, и по лемме 2.2 имеем 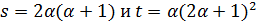 .
.
Если 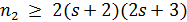 , то ввиду равенства
, то ввиду равенства 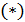 имеем
имеем 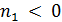 , что абсурдно. Значит,
, что абсурдно. Значит, 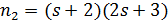 и согласно
и согласно 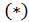 число
число 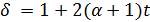 делит
делит 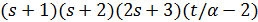 . Далее,
. Далее, 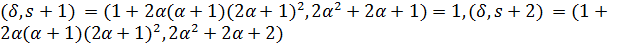 делит 7,
делит 7, 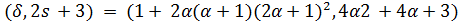 делит 4 и
делит 4 и 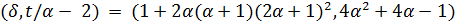 делит 2. Таким образом,
делит 2. Таким образом, 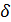 делит 14, противоречие. Лемма 2.3 и теорема 1 доказаны.
делит 14, противоречие. Лемма 2.3 и теорема 1 доказаны.
3. Сильно 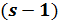 -однородные геометрии
-однородные геометрии
Предположим, что  - сильно
- сильно 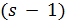 -однородная геометрия
-однородная геометрия 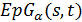 . По лемме 1.2 число
. По лемме 1.2 число 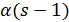 делит
делит 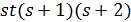 , поэтому
, поэтому 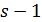 делит
делит 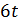 . По лемме 1.3 точечный граф
. По лемме 1.3 точечный граф 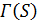 является псевдогеометрическим для частичной геометрии
является псевдогеометрическим для частичной геометрии 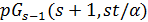 . В частности, он сильно регулярен с параметрами
. В частности, он сильно регулярен с параметрами 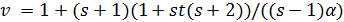 ,
, 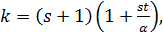 λ
λ 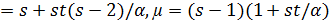 , и
, и 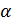 делит
делит 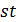 . Далее, собственные значения графа
. Далее, собственные значения графа  равны
равны 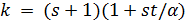 ,
, 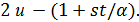 Можно считать, что
Можно считать, что 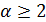 , поэтому
, поэтому 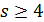 .
.
Лемма 3.1. Верны следующие утверждения:
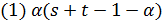 делит
делит 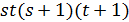 ;
;
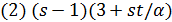 делит
делит 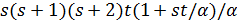 ;
;
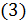 если
если 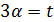 или
или 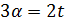 , то
, то  - одна из геометрий
- одна из геометрий 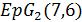 или
или 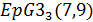 .
.
Доказательство. Утверждения (1–2)-не что иное, как условия целочисленности для 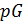 и
и  .
.
Пусть 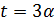 . Тогда
. Тогда 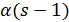 делит
делит 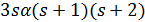 , поэтому
, поэтому 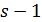 делит 18 и
делит 18 и 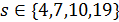 . Кроме того,
. Кроме того, 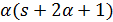 делит
делит 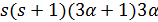 . Вслучае
. Вслучае 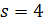 число
число 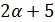 делит
делит 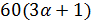 , поэтому
, поэтому 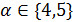 . Противоречие с тем, что
. Противоречие с тем, что 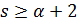 .
.
Если 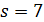 , то
, то 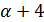 делит
делит 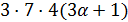 , поэтому
, поэтому 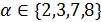 . В этом случае заключение леммы выполняется.
. В этом случае заключение леммы выполняется.
Если 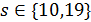 , то 27 делит
, то 27 делит 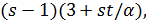 но не делит
но не делит 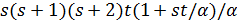 .
.
Пусть теперь 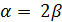 ,
, 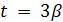 . Тогда
. Тогда 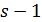 делит 18 и
делит 18 и 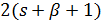 делит
делит 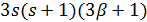 , поэтому
, поэтому 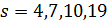 . Таккак 27 делит
. Таккак 27 делит 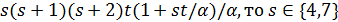 . Если
. Если 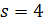 , то
, то 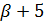 делит
делит 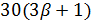 , поэтому
, поэтому 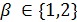 . Но геометрия
. Но геометрия 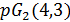 не существует, а
не существует, а 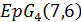 не удовлетворяет условию целочисленности.
не удовлетворяет условию целочисленности.
Если 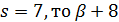 делит
делит 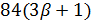 , поэтому
, поэтому 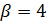 . Противоречие с тем, что
. Противоречие с тем, что 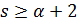 .
.
Лемма 3.2. Либо  есть
есть 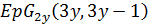 с нечетным
с нечетным 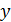 , либо
, либо 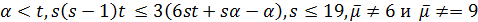 в графе
в графе 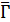 .
.
Доказательство. Напомним, что 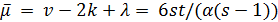 . Если
. Если 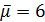 , то
, то 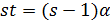 и
и 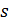 делит
делит 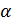 , противоречие.
, противоречие.
Пусть 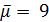 . Тогда
. Тогда 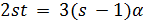 . Следовательно, либо
. Следовательно, либо 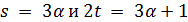 , либо
, либо 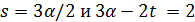 . В первом случае по утверждению (2) леммы 3.1 число
. В первом случае по утверждению (2) леммы 3.1 число 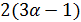 делит
делит 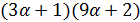 , поэтому
, поэтому 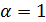 , противоречие. Во втором случае имеем расширение частичной геометрии
, противоречие. Во втором случае имеем расширение частичной геометрии 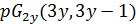 , и по утверждению (1) леммы 3.1число
, и по утверждению (1) леммы 3.1число 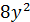 делит
делит 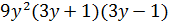 , поэтому
, поэтому 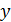 нечетно. В этом случае заключение леммы выполняется.
нечетно. В этом случае заключение леммы выполняется.
Пусть 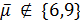 . Используя оценку для числа лап в графе
. Используя оценку для числа лап в графе 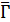 , имеем
, имеем 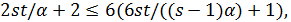 поэтому
поэтому 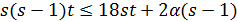 . Значит,
. Значит, 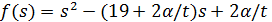 не больше 0, поэтому
не больше 0, поэтому 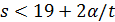 .
.
Если 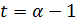 , то
, то 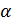 делит
делит 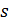 . Следовательно,
. Следовательно, 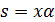 , а также
, а также 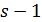 делит
делит 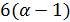 и
и 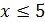 . По утверждению (2) леммы 3.1 число
. По утверждению (2) леммы 3.1 число  делит
делит 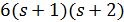 , значит,
, значит,  делит
делит 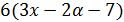 . Для
. Для 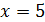 параметр
параметр 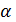 не больше 4, и
не больше 4, и 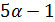 не делит
не делит 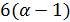 , противоречие. Для
, противоречие. Для 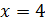 число
число 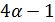 делит 9, а для
делит 9, а для 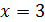 число
число 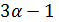 делит 4. В любом случае приходим к противоречию. Наконец, для
делит 4. В любом случае приходим к противоречию. Наконец, для 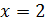 число
число 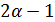 делит 3, и
делит 3, и  есть
есть 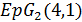 . Противоречие с леммой 1.4.
. Противоречие с леммой 1.4.
Если 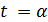 , то
, то 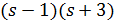 делит
делит 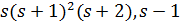 и
и 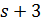 делят 12, поэтому
делят 12, поэтому 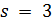 . Но в этом случае
. Но в этом случае 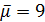 , противоречие.
, противоречие.
Пусть теперь 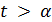 .
. 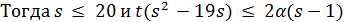 . Если
. Если 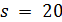 , то
, то 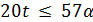 и
и 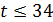 . Далее,
. Далее, 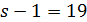 делит
делит 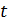 , поэтому
, поэтому 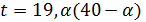 делит
делит 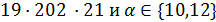 . Но
. Но 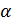 делит
делит 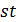 , поэтому
, поэтому 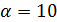 , противоречие с утверждением (2) леммы 3.1. Лемма доказана.
, противоречие с утверждением (2) леммы 3.1. Лемма доказана.
Будем предполагать, что 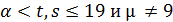 .
.
Лемма 3.3. Если 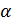 делит
делит 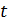 , то
, то 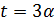 .
.
Доказательство. Пусть 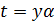 . Тогда
. Тогда 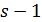 делит
делит 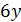 , и по утверждению (2) леммы 3.1 число
, и по утверждению (2) леммы 3.1 число 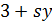 делит
делит 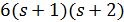 , поэтому
, поэтому 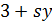 делит
делит 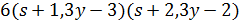 .
.
В случае 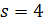 число
число 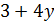 делит
делит 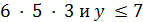 , поэтому
, поэтому 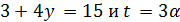 . В случае
. В случае 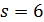 число
число 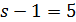 делит
делит 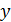 ,
, 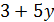 делит 6·7·8.
делит 6·7·8. 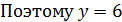 , и 11 не делит 7·8. В случае
, и 11 не делит 7·8. В случае 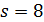 число
число 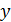 делится на 7 и
делится на 7 и 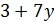 делит 6·9·10. Поэтому
делит 6·9·10. Поэтому 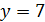 и 24 не делит
и 24 не делит 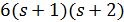 . В случае
. В случае 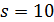 имеем y
имеем y 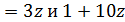 делит 11 · 12. Значит,
делит 11 · 12. Значит, 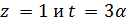 . В случае
. В случае 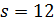 имеем
имеем 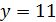 , и 45 не делит 13 · 14, противоречие.
, и 45 не делит 13 · 14, противоречие.
Если 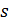 четно, то либо 3 делит
четно, то либо 3 делит 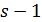 , либо
, либо 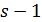 делит
делит 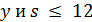 . Следовательно,
. Следовательно, 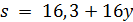 делит
делит 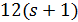 , поэтому
, поэтому 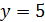 или 10, и
или 10, и 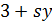 не делит
не делит 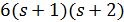 .
.
Значит, 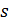 нечетно. Если
нечетно. Если 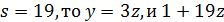 делит 3 · 5 · 7, противоречие.
делит 3 · 5 · 7, противоречие.
В случае 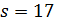 число 8 делит y и 3+17y делит 6 · 18 · 19, противоречие.
число 8 делит y и 3+17y делит 6 · 18 · 19, противоречие.
В случае 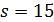 число 7 делит
число 7 делит 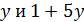 делит 2 · 16 · 17, противоречие.
делит 2 · 16 · 17, противоречие.
В случае 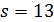 число
число 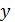 четно
четно 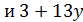 делит 3 · 7 · 15, противоречие.
делит 3 · 7 · 15, противоречие.
В случае 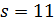 число 5 делит
число 5 делит 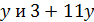 делит 6 · 12 · 13, противоречие.
делит 6 · 12 · 13, противоречие.
В случае 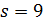 число 4 делит
число 4 делит 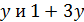 делит 5 · 11, противоречие.
делит 5 · 11, противоречие.
В случае 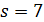 число
число 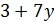 делит 6 · 8 · 9, поэтому
делит 6 · 8 · 9, поэтому 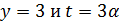 .
.
В случае 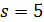 число
число 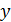 четно и
четно и 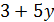 делит 3·3·7, поэтому
делит 3·3·7, поэтому 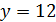 и в псевдогеометрическом графе для
и в псевдогеометрическом графе для 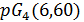 условия целочисленности выполнены. Однако в этом случае имеем
условия целочисленности выполнены. Однако в этом случае имеем 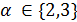 и в геометриях
и в геометриях 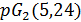 ,
, 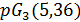 условия целочисленности нарушаются.
условия целочисленности нарушаются.
Лемма 3.4. Если 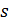 нечетно, то геометрия
нечетно, то геометрия  есть либо
есть либо 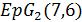 , либо
, либо 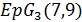 .
.
Доказательство. Если 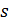 - простое число, то
- простое число, то  делит
делит  , и ввиду лемм 3.1 и 3.3 заключение леммы выполняется.
, и ввиду лемм 3.1 и 3.3 заключение леммы выполняется.
Пусть 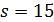 . Тогда
. Тогда 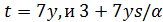 делит 6·16·17. Если 3 делит
делит 6·16·17. Если 3 делит 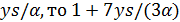 делит 25 · 17, противоречие. Значит, 3 не делит
делит 25 · 17, противоречие. Значит, 3 не делит 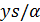 , и
, и 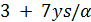 делит 25 · 17. Поэтому
делит 25 · 17. Поэтому 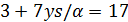 или 8 · 17. Значит,
или 8 · 17. Значит, 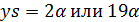 . В любом случае s делит α, противоречие.
. В любом случае s делит α, противоречие.
Пусть 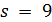 . Тогда 4 делит
. Тогда 4 делит 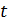 , и по лемме 3.3 число 3 делит
, и по лемме 3.3 число 3 делит 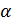 . Следовательно,
. Следовательно, 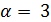 или 6, кроме того,
или 6, кроме того, 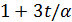 делит 5 · 11. Поэтому
делит 5 · 11. Поэтому 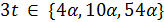 . В первом случае
. В первом случае 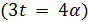 либо
либо 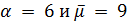 , либо
, либо 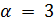 , и 11 не делит
, и 11 не делит 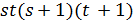 . Во втором случае получим противоречие с утверждением (2) леммы 3.1. В третьем случае α
. Во втором случае получим противоречие с утверждением (2) леммы 3.1. В третьем случае α 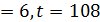 , противоречие с утверждением (1) леммы 3.1. Лемма доказана.
, противоречие с утверждением (1) леммы 3.1. Лемма доказана.
В леммах 3.5–3.8 будем предполагать, что 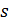 четно.
четно.
Лемма 3.5. Если 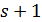 взаимно просто с
взаимно просто с 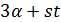 , то
, то  есть
есть 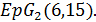
Доказательство. Пусть 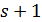 взаимно просто с
взаимно просто с 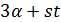 . По лемме 3.1 число
. По лемме 3.1 число 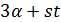 делит
делит 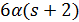 . Тогда
. Тогда 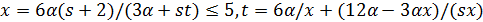 и 3 делит
и 3 делит 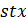 . В случае
. В случае 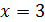 имеем
имеем 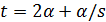 , противоречие. Поэтому
, противоречие. Поэтому 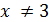 и 3 делит
и 3 делит 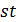 .
.
Пусть 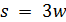 . Тогда
. Тогда 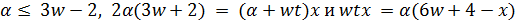 . Так как
. Так как 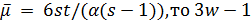 делит
делит 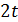 . В случае
. В случае 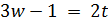 получим
получим 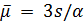 , поэтому
, поэтому 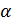 взаимно просто с
взаимно просто с 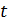 и
и 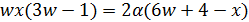 . Отсюда
. Отсюда 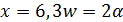 и число
и число 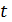 не целое. Значит,
не целое. Значит, 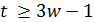 .
.
Если 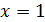 , то
, то 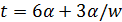 и
и 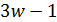 делит
делит 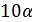 . В случае
. В случае 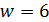 имеем
имеем 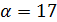 , противоречие. В случае
, противоречие. В случае 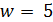 имеем
имеем 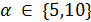 и 7 не делит
и 7 не делит 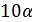 . В случае
. В случае 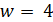 имеем
имеем 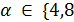 } и 11 не делит
} и 11 не делит 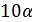 . В случае
. В случае 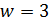 имеем
имеем 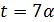 и 8 не делит
и 8 не делит 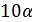 , поэтому α
, поэтому α 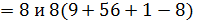 не делит
не делит 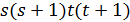 . В случае
. В случае 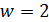 имеем
имеем 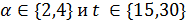 . Так как
. Так как 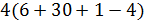 не делит
не делит 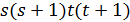 , то
, то  является расширением геометрии
является расширением геометрии 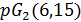 .
.
Если 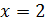 , то
, то 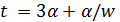 и
и 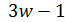 делит
делит 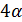 . Поэтому α
. Поэтому α 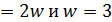 , противоречие с тем, что
, противоречие с тем, что 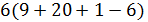 не делит
не делит 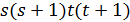 .
.
Если 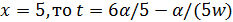 , противоречие.
, противоречие.
Итак, 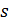 не делится на 3, поэтому 3 делит
не делится на 3, поэтому 3 делит 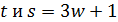 . Тогда
. Тогда
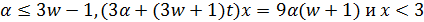 .
.
Если 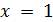 , то
, то 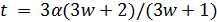 , противоречие. Если
, противоречие. Если 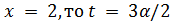 ,
, 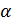 четно и
четно и 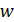 нечетно. Так как
нечетно. Так как 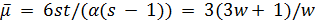 , то
, то 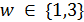 . Если
. Если 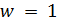 , то
, то 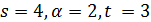 , противоречие с тем, что частичная геометрия
, противоречие с тем, что частичная геометрия 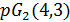 не существует. Если
не существует. Если 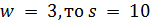 ,
, 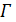 является псевдогеометрическим графом для
является псевдогеометрическим графом для 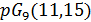 и нарушается условие целочисленности.
и нарушается условие целочисленности.
Лемма 3.6. Если 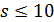 , то
, то  является геометрией
является геометрией 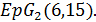
Доказательство. Пусть 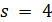 . Тогда
. Тогда 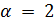 и
и 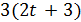 делит
делит 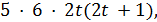 кроме того, по лемме 3.5 простое число 5 делит
кроме того, по лемме 3.5 простое число 5 делит 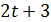 . Следовательно,
. Следовательно, 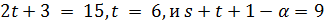 не делит
не делит 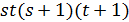 .
.
Пусть 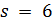 . По лемме 3.5 число 7 делит
. По лемме 3.5 число 7 делит 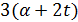 . Если
. Если 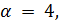 то
то 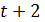 делится на 7 и
делится на 7 и 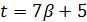 . Далее,
. Далее, 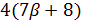 делит
делит 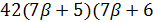 ) и
) и 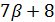 делит 126, противоречие.
делит 126, противоречие.
Если 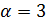 , то
, то 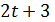 делится на 7 и
делится на 7 и 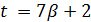 . Далее,
. Далее, 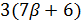 делит
делит 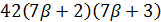 и
и 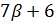 делит 84, поэтому
делит 84, поэтому 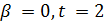 и
и 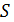 является расширением геометрии
является расширением геометрии 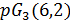 . Но в этом случае по лемме 1.2 число
. Но в этом случае по лемме 1.2 число 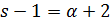 должно быть четно, противоречие.
должно быть четно, противоречие.
Если 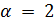 , то
, то 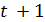 делится на 7 и
делится на 7 и 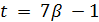 . Далее,
. Далее, 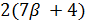 делит
делит 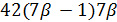 и
и 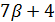 делит 21 · 20, поэтому
делит 21 · 20, поэтому 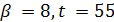 , противоречие с тем, что геометрия
, противоречие с тем, что геометрия 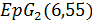 не удовлетворяет условию Крейна.
не удовлетворяет условию Крейна.
Пусть 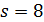 . Так как
. Так как 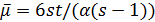 , то 7 делит
, то 7 делит 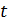 и
и 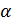 четно (так как
четно (так как 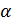 делит
делит 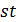 , но не делит
, но не делит 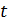 ). По лемме 3.5 число 3 делит
). По лемме 3.5 число 3 делит 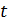 , поэтому
, поэтому 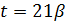 .
.
Если 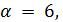 то
то 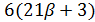 делит
делит 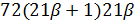 и
и 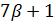 делит
делит 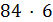 , поэтому
, поэтому 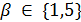 . В случае
. В случае 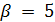 число
число 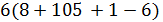 не делит
не делит 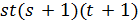 . В случае
. В случае 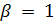 число
число 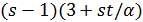 не делит
не делит 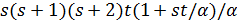 , противоречие.
, противоречие.
Если 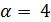 , то
, то 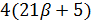 делит
делит 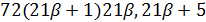 делит
делит 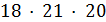 , поэтому
, поэтому 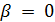 , противоречие. Если
, противоречие. Если 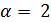 , то
, то 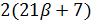 делит
делит 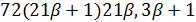 делит
делит 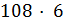 , поэтому
, поэтому 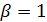 , противоречие с тем, что
, противоречие с тем, что 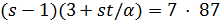 не делит
не делит 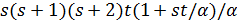 .
.
Пусть 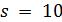 . Тогда
. Тогда 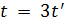 для некоторого целого числа
для некоторого целого числа 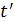 , и 11 делит
, и 11 делит 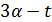 . Поэтому
. Поэтому 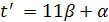 . Если
. Если 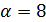 , то
, то 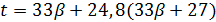 делит
делит 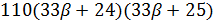 и
и 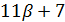 делит
делит 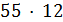 , противоречие.
, противоречие.
Если 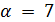 , то
, то 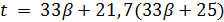 делит
делит 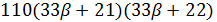 и
и 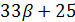 делит
делит 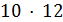 , противоречие.
, противоречие.
Если 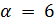 , то
, то 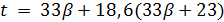 делит
делит 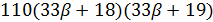 и
и 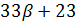 делит
делит 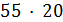 , противоречие.
, противоречие.
Если 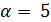 , то
, то 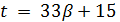 и
и 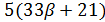 делит
делит 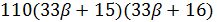 и
и 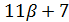 делит
делит 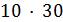 , противоречие.
, противоречие.
Если 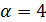 , то
, то 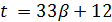 и
и 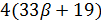 делит
делит 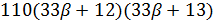 и
и 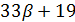 делит
делит 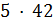 , противоречие.
, противоречие.
Если 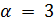 , то
, то 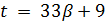 и
и 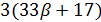 делит
делит 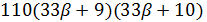 и
и 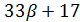 делит
делит 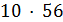 , противоречие.
, противоречие.
Если 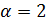 , то
, то 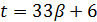 и
и 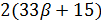 делит
делит 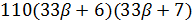 и
и 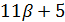 делит
делит 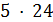 , поэтому
, поэтому 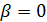 и
и 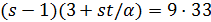 не делит
не делит 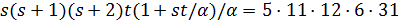 .
.
Лемма 3.7. Если 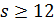 , то
, то 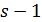 делит
делит 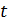 , и
, и 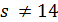 .
.
Доказательство. Пусть 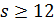 . Если
. Если 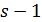 не делит
не делит 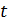 , то
, то 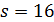 и 3 не делит
и 3 не делит 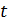 . Но в этом случае
. Но в этом случае 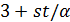 взаимно просто с 6, и
взаимно просто с 6, и 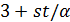 делит 17, противоречие.
делит 17, противоречие.
Пусть 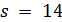 . Тогда 13 делит
. Тогда 13 делит 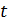 , и либо
, и либо 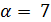 , либо
, либо 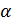 четно. Если
четно. Если 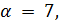 то
то 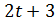 делит
делит 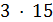 , противоречие.
, противоречие.
Если 3 делит 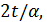 то
то 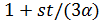 делит
делит 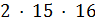 . Но
. Но 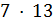 не делит
не делит 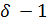 для любого делителя
для любого делителя 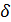 числа
числа 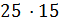 . Значит, 3 не делит
. Значит, 3 не делит 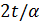 , и
, и 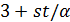 делит
делит 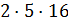 . Как и выше, пришли к противоречию.
. Как и выше, пришли к противоречию.
Лемма 3.8. Параметр 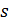 меньше 12.
меньше 12.
Доказательство. Пусть 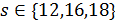 . Согласно леммам 3.5, 3.7 число
. Согласно леммам 3.5, 3.7 число 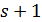 делит
делит 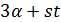 , и
, и 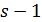 делит
делит 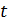 . Если 3 не делит
. Если 3 не делит 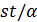 , то
, то 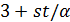 делит
делит 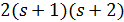 . Пусть
. Пусть 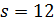 . Тогда 3 делит
. Тогда 3 делит 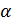 , и
, и 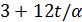 делит
делит 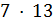 . Значит,
. Значит, 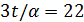 и
и 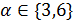 (
( 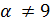 по лемме 1.2). Следовательно,
по лемме 1.2). Следовательно, 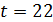 или 44, но в каждом случае
или 44, но в каждом случае 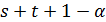 не делит
не делит 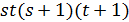 . Если
. Если 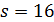 , то
, то 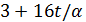 делит 17, противоречие. Пусть
делит 17, противоречие. Пусть 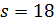 . Тогда
. Тогда 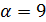 , и 3 не делит
, и 3 не делит 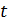 , так что
, так что 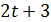 делит
делит 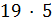 . Противоречие с тем, что 17 делит
. Противоречие с тем, что 17 делит 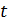 .
.
Таким образом, 3 делит 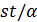 , и
, и 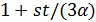 делит
делит 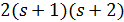 . Пусть
. Пусть 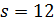 . Тогда 11 делит
. Тогда 11 делит 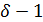 для некоторого делителя
для некоторого делителя 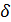 числа
числа 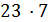 . Поэтому
. Поэтому 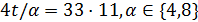 и
и 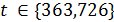 . Но в первом случае нарушается условие Крейна, а во втором число
. Но в первом случае нарушается условие Крейна, а во втором число 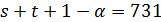 не делит
не делит 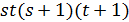 .
.
Пусть 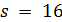 . Тогда
. Тогда 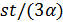 является четным, и
является четным, и 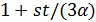 делит
делит  . Если
. Если 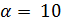 , то
, то 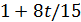 делит
делит 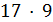 и
и 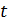 нечетно. Значит,
нечетно. Значит, 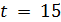 или
или 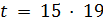 . В любом из этих случаев
. В любом из этих случаев 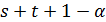 не делит
не делит 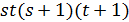 . Поэтому 5 не делит
. Поэтому 5 не делит 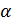 , и 5 делит
, и 5 делит 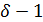 для некоторого
для некоторого 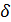 , являющегося делителем числа
, являющегося делителем числа  . Следовательно,
. Следовательно, 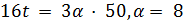 и
и 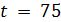 . В этом случае
. В этом случае 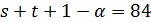 не делит
не делит 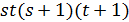 .
.
Пусть 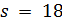 . Тогда
. Тогда 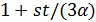 делит
делит 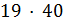 , и 17 делит
, и 17 делит 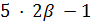 для
для 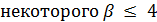 , противоречие. Лемма доказана.
, противоречие. Лемма доказана.
Леммы 3.4, 3.6 и 3.8 доказывают теорему 2.
Список литературы
1. Cameron P. J., Hughes D. R., Pasini A. Extended generalized quadrangles // Geom. Dedicata. 1990. V. 35. P. 193–228.
2. Thas J. A. Some results on quadrics and newpartial geometries // Simon Stevin. 1981. V. 55. P. 129–139.
3. Hobart S. A., Hughes D. R. Extended partial geometries: nets and dual nets // Europ. J. Comb. 1990. V. 11. P. 357–372.
4. Hobart S. A., Hughes D. R. 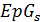 withminimal µ. II //Geom. Dedicata. 1992.
withminimal µ. II //Geom. Dedicata. 1992.
V. 42. P. 129–138.
5. HughesD. R. Extended partial geometries: dual 2-design //Europ. J. Comb. 1990. V. 11. P. 459–472.
6. Seidel J. J. Strongly regular graphs with (−1,1,0) adjacency matrix having eigenvalue 3 // Linear Algebra&Appl. 1968. V. 1. P. 281–298.
7. Brouwer A. E., Lint J. H. van. Strongly regular graphs and partial geometries // Enumeration&Design / Eds. D. Jackson, S. Vanstone. NewYork: Academic Press, 1984. P. 85–122.








