Математический факультет
Министерство образования и науки РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«КАБАРДИНО-БАЛКАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ им. Х.М. БЕРБЕКОВА»
МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ
Карданова Милана Беслановна
ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА
« О 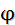 - однородных расширениях частичных геометрий с большим
- однородных расширениях частичных геометрий с большим 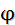 »
»
Научный руководитель:
к.ф.-м.н.,доцент каф. ГиВА ………………………………………….… Нирова М.С.
Рецензент:
к.ф.-м.н., доцент каф.
вычислит.математики………………………………………………………...…. Кудаев В.Ч.
Допущена к защите «____»_________________2014г.
Зав.каф. ГиВА
д.ф.-м.н., профессор……………………………………………………………... Журтов А.Х.
Нальчик 2014г.
Содержание
Введение………………………………………………………………………….3
§ 1. Принятые обозначения и определения …………………………………….
§ 2. Об однородных расширениях частичных геометрий……………….……
1. Предварительные результаты…………………………………………….
2. Случай 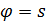 ……………………………………………………………….
……………………………………………………………….
3. Сильно 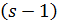 - однородные геометрии………………………………….
- однородные геометрии………………………………….
§ 3.…………………………………...
Заключение…………………………………………………………………………
Список литературы………………………………………………………………
§ 1. Принятые обозначения и определения .
· Граф G – это пара множеств 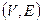 , где
, где 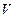 - множество вершин, а
- множество вершин, а 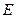 - множество ребер. Вершины и рёбра графа называются его элементами.
- множество ребер. Вершины и рёбра графа называются его элементами.
· Число вершин графа G называется его порядком и обозначается через 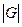 . Если
. Если 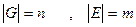 , то G называют
, то G называют 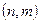 - графом.
- графом.
· Говорят, что две вершины 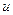 и
и 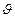 смежны, если множество
смежны, если множество 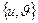 является ребром, и не смежны в противном случае. Если
является ребром, и не смежны в противном случае. Если 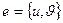 - ребро, то вершины
- ребро, то вершины 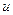 и
и 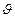 называют его концами. Два ребра ребра называются смежными, если они имеют общий конец.
называют его концами. Два ребра ребра называются смежными, если они имеют общий конец.
· Вершина 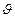 и ребро
и ребро 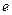 называются инцидентными, если
называются инцидентными, если 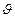 является концом ребра
является концом ребра 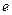 ( т.е.
( т.е. 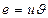 ), и не инцидентными в противном случае.
), и не инцидентными в противном случае.
· Множество всех вершин графа G , смежных с вершиной 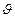 называется окрестностью вершины
называется окрестностью вершины 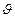 и обозначается через
и обозначается через 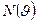 .
.
· Граф G называется полным, если любые две его вершины смежны , т.е. 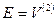 . Полный граф порядка
. Полный граф порядка 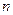 обозначают символом
обозначают символом 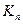 число рёбер в нём равно
число рёбер в нём равно
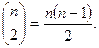
· Граф G называется пустым, если в нём нет рёбер. Пустой граф порядка 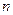 обозначается через
обозначается через 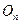 .
.
· Граф G называется двудольным, если множество его вершин разбито на части (доли ) так, что концы каждого ребра принадлежат разным частям (долям). Если при этом любые две вершины, входящие в разные доли, смежны, то граф называется полным двудольным .
Полный двудольный граф, доли которого состоят из 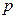 и из
и из 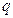 вершин, обозначается
вершин, обозначается 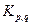 .
.
Аналогично двудольным определяются 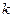 -дольный и полный
-дольный и полный 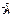 -дольный графы для
-дольный графы для 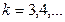 .
.
Легко подсчитать число всех графов с фиксированным множеством вершин 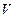 . Эти графы различаются своими рёбрами, и поэтому их число равно количеству подмножеств в
. Эти графы различаются своими рёбрами, и поэтому их число равно количеству подмножеств в 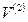 , т.е.
, т.е.
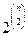 , где
, где 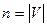 .
.
· Мультиграф – это пара 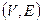 , где
, где 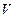 - множество вершин, а
- множество вершин, а 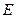 - семейство множеств множества
- семейство множеств множества 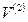 (рёбер).
(рёбер).
Употребление термина «семейства» вместо «множество »означает, что элементы множества 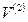 могут в
могут в 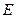 повторятся, т.е. допускаются кратные рёбра.
повторятся, т.е. допускаются кратные рёбра.
· Петли – это рёбра соединяющие вершину саму с собой. Если допускаются петли и кратные рёбра, получаем псевдограф.
· Ориентированный граф (или орграф) – это пара 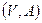 , где
, где 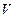 - множество вершин,
- множество вершин, 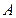 - множество ориентированных рёбер, которые называются дугами,
- множество ориентированных рёбер, которые называются дугами, 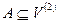 . Если
. Если 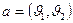 - дуга, то вершины
- дуга, то вершины 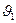 и
и 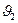 называются её началом и концом.
называются её началом и концом.
· Направленный граф – это орграф, не имеющий симметричных (т.е. дуг вида 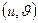 и
и 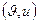 ) пар ориентированных рёбер.
) пар ориентированных рёбер.
· Два графа G и Н изоморфны 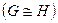 , если между их множеством вершин существует взаимно однозначное соответствие, сохраняющие смежность.
, если между их множеством вершин существует взаимно однозначное соответствие, сохраняющие смежность.
· Изоморфизм есть отношение эквивалентности на графах.
· Подграфом G называется граф, у которого все вершины и рёбра принадлежат G 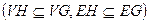 .
.
· Остовый граф – это подграф графа G, содержащий все его вершины (т.е. 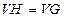 ). Если множество вершин подграфа Н есть
). Если множество вершин подграфа Н есть 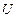 , а множество его рёбер совпадает с множеством всех рёбер графаG, оба конца которых принадлежат
, а множество его рёбер совпадает с множеством всех рёбер графаG, оба конца которых принадлежат 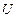 ,то Н называется подграфом, порождённым множеством
,то Н называется подграфом, порождённым множеством 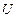 , и обозначается через
, и обозначается через 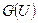 .
.
· Матрицей смежности графа G с множеством вершин 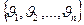 называется матрица
называется матрица 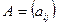 ,
, 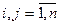 (т.е.
(т.е. 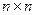 ), в которой элемент
), в которой элемент 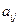 равен числу рёбер в G , соединяющих
равен числу рёбер в G , соединяющих 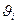 и
и 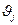 .
.
Удаление вершины или ребра, а также переход к другому подграфу – это операции, с помощью которых можно из имеющегося графа получать другие графы с меньшим числом элементов. Известны так же операции позволяющие увеличить число элементов графа. Например, операция добавления ребра: если вершины 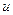 и
и 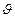 не смежны, то можно определить граф
не смежны, то можно определить граф 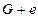 , где
, где 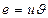 . Он получается из графа G добавлением ребра
. Он получается из графа G добавлением ребра 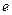 .
.
· Граф 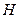 называется объединением графов
называется объединением графов 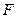 и
и 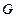 , если
, если 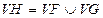 и
и 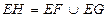 (или
(или 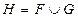 ). Объединение
). Объединение 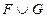 называется дизъюнктивным, если
называется дизъюнктивным, если 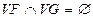 , т.е. никакие два из объединяемых графов не должны иметь общих вершин .
, т.е. никакие два из объединяемых графов не должны иметь общих вершин .
· Говорят, что графы 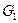 и
и 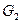 соединены (обозначается
соединены (обозначается 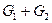 ), если состоит из
), если состоит из 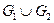 и всех рёбер соединяющих
и всех рёбер соединяющих 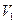 и
и 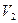 . В частности ,
. В частности , 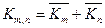 , где
, где
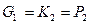 и
и 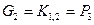 .
.
· Произведением графов 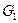 и
и 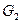 (обозначается
(обозначается 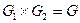 ) называется граф, для которого
) называется граф, для которого 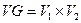 - декартово произведения множеств вершин исходных графов, а
- декартово произведения множеств вершин исходных графов, а 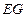 определяется так: вершины
определяется так: вершины 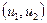 и
и 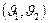 смежны в G тогда и только тогда, когда или
смежны в G тогда и только тогда, когда или 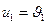 , а
, а 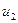 и
и 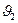 смежны в
смежны в 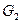 , или
, или 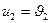 , а
, а 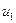 и
и 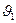 смежны в
смежны в 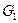 .
.
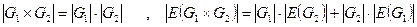
С помощью операции произведения вводится важный класс графов - 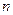 -мерные кубы
-мерные кубы 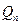 . Он определяется рекуррентно:
. Он определяется рекуррентно:
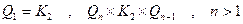 .
.
· 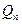 - это граф порядка
- это граф порядка 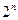 , вершины которого можно представить
, вершины которого можно представить 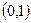 - векторами длины
- векторами длины 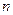 таким образом, что две вершины будут смежны тогда и только тогда, когда соответствующие векторы различаются ровно в одной координате. Поскольку каждая вершина
таким образом, что две вершины будут смежны тогда и только тогда, когда соответствующие векторы различаются ровно в одной координате. Поскольку каждая вершина 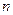 -мерного куба инцидентна
-мерного куба инцидентна 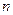 - ребрам, то число его рёбер равно
- ребрам, то число его рёбер равно 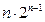 .
.
Ещё одна важная операция – отождествление (или слияние) вершин. Пусть 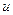 и
и 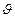 две вершины графа G,
две вершины графа G, 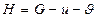 . К графу присоединим новую вершину
. К графу присоединим новую вершину 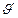 , соединив её ребром с каждой из вершин, входящих в объединение окружений вершин
, соединив её ребром с каждой из вершин, входящих в объединение окружений вершин 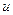 и
и 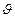 в графе G . Говорят, что построенный граф получается из графа G отождествлением вершин
в графе G . Говорят, что построенный граф получается из графа G отождествлением вершин 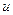 и
и 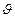
· Граф G называется стягиваемым к графу Н, если Н получается из G в результате некоторой последовательности стягивания рёбер.
Например, граф Петерсена стягиваем к 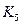 и стало быть к любому
и стало быть к любому 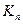 с
с 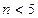 . Любой непустой связный граф отличный от
. Любой непустой связный граф отличный от 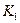 стягиваем к
стягиваем к 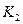 . Но уже не любой связный граф стягивается к
. Но уже не любой связный граф стягивается к 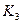 . Например, простая цеп
. Например, простая цеп 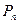 не стягивается к
не стягивается к 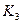 . Поэтому возникает параметр
. Поэтому возникает параметр 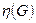 - максимум порядков полных графов к которым стягивается граф G. Параметр
- максимум порядков полных графов к которым стягивается граф G. Параметр 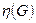 называется Хадвигера графа G .
называется Хадвигера графа G .
· Степенью вершины называют количество входящих в вершину рёбер.
· Путём в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершиной ребром.
· Циклом называют путь, в котором первая и последняя вершины соединены ребром.
· Деревом называют связный граф без циклов.
· Расстоянием 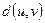 между вершинами
между вершинами 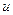 и
и 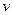 графа Г называется длина кратчайшей простой цепи, соединяющей их; если
графа Г называется длина кратчайшей простой цепи, соединяющей их; если 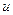 и
и 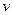 не соединены, то полагаем
не соединены, то полагаем 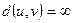
· Степенью вершины 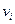 в графе Г – обозначается
в графе Г – обозначается 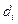 или
или 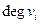 - называется число рёбер, инцидентных
- называется число рёбер, инцидентных 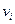
· Непустое множество А вместе с заданной на нем бинарной операцией (·) образует группу, если выполнены следующие четыре аксиомы:
Аксиома 1 (замыкание). Для любых двух элементов а и в, принадлежащих множеству А, элемент а · в принадлежит А.
Аксиома 2(ассоциативности) Для любых трёх элементов а,в,с, принадлежащих множеству А, справедливо равенство а·(в·с)=(а·в) ·с.
Аксиома 3 (тождественности). В множестве А существует такой элемент е, что е·а=а·е=а, для всех элементов а из А.
Аксиома 4 (обращения). Если выполняется аксиома 3, то для любого элемента а, принадлежащего множеству А, существует элемент, обозначаемый 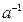 , такой, что
, такой, что 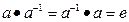 .
.
· Взаимно однозначное отображение конечного множества на себя называется подстановкой.
· Автоморфизмом графа Г называется изоморфизм графа Г на себя. Таким образом, каждый автоморфизм 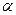 графа Г есть подстановка множества вершин V, сохраняющая смежность.
графа Г есть подстановка множества вершин V, сохраняющая смежность.
· Неориентированный 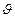 - вершинный граф, в котором степени всех вершин равны
- вершинный граф, в котором степени всех вершин равны 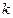 , а каждое ребро принадлежит точно
, а каждое ребро принадлежит точно 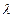 треугольникам, называется рёберно регулярным с параметрами
треугольникам, называется рёберно регулярным с параметрами 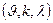 . Положим
. Положим 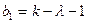 . Сильно регулярным графом с параметрами
. Сильно регулярным графом с параметрами 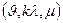 называется рёберно регулярный граф с соответствующими параметрами, в котором пересечение окрестностей любых несмежных вершин содержащих точно
называется рёберно регулярный граф с соответствующими параметрами, в котором пересечение окрестностей любых несмежных вершин содержащих точно 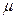 вершин .
вершин .
· Пара 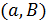 , из
, из 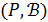 , называется флагом, если точка
, называется флагом, если точка 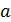 принадлежит блоку
принадлежит блоку 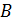 , и антифлагом в противном случае. Если
, и антифлагом в противном случае. Если 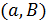 является антифлагом, то через
является антифлагом, то через 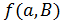 обозначим число точек в
обозначим число точек в 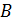 , коллинеарных
, коллинеарных 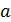 . Геометрия называется
. Геометрия называется 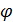 – однородной (
– однородной ( 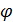 – натуральное число), если для любого антифлага
– натуральное число), если для любого антифлага 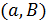 число
число 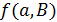 равно 0 или
равно 0 или 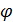 , и сильно
, и сильно 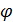 - однородной, если это число всегда равно
- однородной, если это число всегда равно 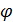 .
.
· Если 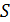 есть такая геометрия точек и прямых, что каждая прямая имеет ровно
есть такая геометрия точек и прямых, что каждая прямая имеет ровно 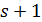 точку, каждая точка лежит ровно на
точку, каждая точка лежит ровно на 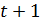 прямой
прямой 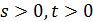 и
и 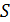 является сильно -однородной
является сильно -однородной 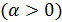 то тогда
то тогда 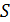 называется
называется 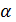 - частичной геометрией порядка
- частичной геометрией порядка 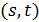 (для краткости
(для краткости 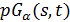 или даже
или даже 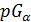 ). Связное расширение семейства частичных геометрий
). Связное расширение семейства частичных геометрий 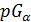 обозначается как
обозначается как 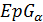 (или даже
(или даже 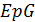 ).
).
· Блоки геометрии 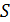 называются прямыми, если различные блоки пересекаются не более чем в одной точке.
называются прямыми, если различные блоки пересекаются не более чем в одной точке.
· Вычет 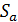 геометрии
геометрии 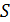 в точке
в точке 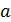 – это геометрия
– это геометрия 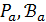 ранга 2, где
ранга 2, где 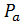 – множество всех точек, коллинеарных
– множество всех точек, коллинеарных 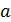 , и
, и 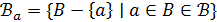 . Пусть
. Пусть 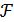 - семейство геометрий ранга 2, и всякий вычет
- семейство геометрий ранга 2, и всякий вычет 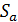 лежит в
лежит в 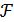 . Тогда говорят, что S является расширением
. Тогда говорят, что S является расширением 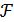 .
.
· Геометрия 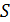 называется треугольной, если для любых попарно коллинеарных точек
называется треугольной, если для любых попарно коллинеарных точек 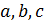 найдется блок, содержащий все три точки
найдется блок, содержащий все три точки 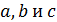 .
.
· Если 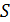 - частичная геометрия
- частичная геометрия 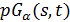 , то двойственная геометрия
, то двойственная геометрия 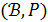 , в которой каждая точка отождествляется с пучком проходящих через нее прямых, является частичной геометрией
, в которой каждая точка отождествляется с пучком проходящих через нее прямых, является частичной геометрией 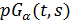 . Обобщенный четырехугольник
. Обобщенный четырехугольник 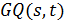 - это частичная геометрия
- это частичная геометрия 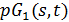 . Геометрия
. Геометрия 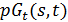 является сетью, а
является сетью, а 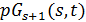 является 2-схемой с
является 2-схемой с 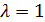 . Коклика из
. Коклика из 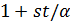 точек в точечном графе геометрии
точек в точечном графе геометрии 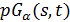 называется овоидом.
называется овоидом.








