5. Конечно-разностные уравнения.
6. Результаты вычислений в виде объемной картинки, полученные по аналитическим формулам и с помощью МКР.
7. Построить на одних осях графики 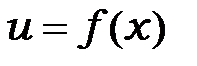 , полученные по аналитическим формулам и с помощью МКР, в моменты времени
, полученные по аналитическим формулам и с помощью МКР, в моменты времени 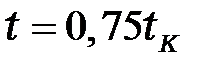 ;
; 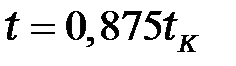 ;
; 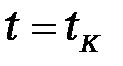 .
.
8. Найти максимальную невязку между аналитическим решением и решением МКР с указанием координаты.
9. Код программы
10. Выводы
2. Решение уравнения параболического типа
Уравнения с частными производными 2-го порядка параболического типа наиболее часто встречаются при изучении процессов теплопроводности и диффузии. Простейшим уравнением параболического типа является уравнение нестационарной теплопроводности для однородного стержня (плоской бесконечной стенки)
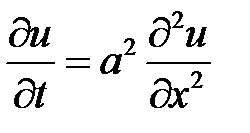 , (2.1)
, (2.1)
где 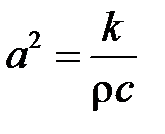 – коэффициент температуропроводности;
– коэффициент температуропроводности; 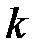 – коэффициент теплопроводности;
– коэффициент теплопроводности; 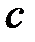 – удельная теплоемкость;
– удельная теплоемкость; 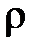 – плотность среды.
– плотность среды.
Начальные условия
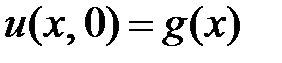 . (2.2)
. (2.2)
Граничным условия
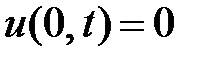 ;
; 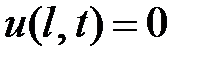 . (2.3)
. (2.3)
Решение уравнения (2.1), полученное аналитически методом разделения переменных (метод Фурье) и удовлетворяющее условиям однозначности (краевым условия) (2.2), (2.3), имеет вид
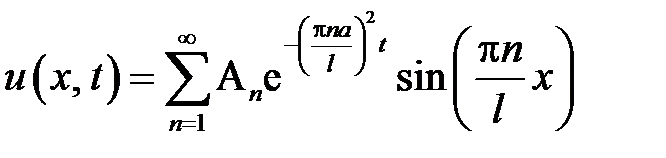 , (2.4)
, (2.4)
На рис. 2.1 показано распределение температуры в стержне в нулевой момент времени
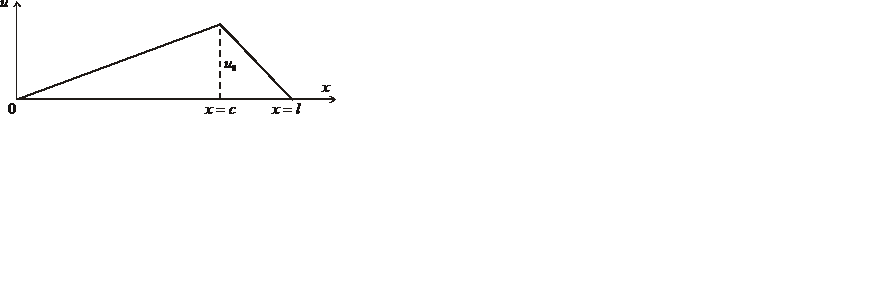
Рис. 1.2. Распределение температуры в стержне в нулевой момент времени
Тогда 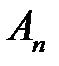 в уравнении (2.4) определяются следующим образом
в уравнении (2.4) определяются следующим образом
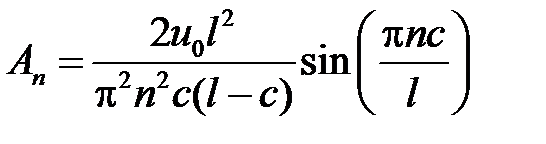 . (2.5)
. (2.5)
Решение задачи гиперболического уравнения (1.1) методом конечных разностей (МКР).
Рассмотрим решение поставленной задачи МКР по явной схеме:
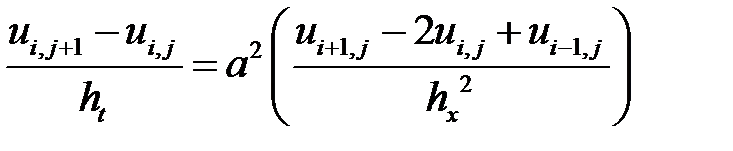 ,
, 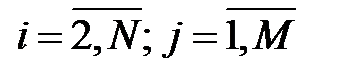 . (2.6)
. (2.6)
На рис. 2.2 шаблон явной схемы показан пунктирной линией.
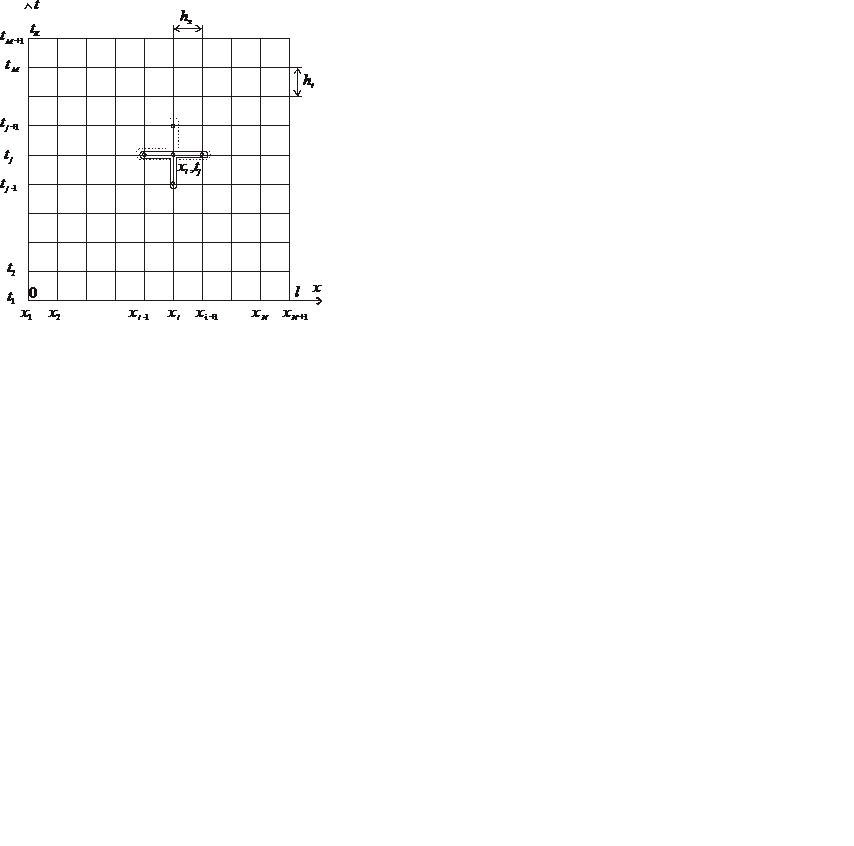
Рис. 2.2. Конечно-разностная сетка
Для решения задачи уравнение (2.6) преобразуется к виду
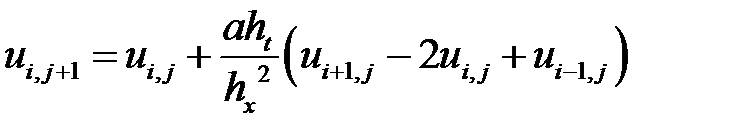 ,
, 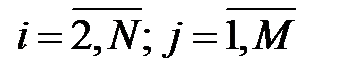 . (2.7)
. (2.7)
Явная конечно-разностная схема (2.6) для параболического уравнения является устойчивой при условии 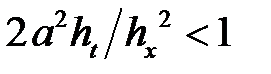 .
.
Для временного слоя 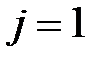 значения функции в узлах сетки определяются из начального условия
значения функции в узлах сетки определяются из начального условия
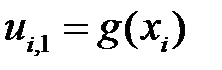 ,
, 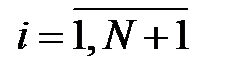 . (2.8)
. (2.8)
Граничные условия (2.3) на левой и правой границах задаются следующим образом: 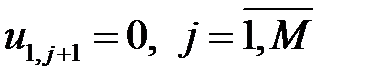 ;
; 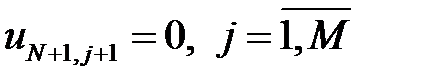 .
.
Решение дифференциального уравнения (2.1) МКР, записанного по неявной схеме, имеет вид:
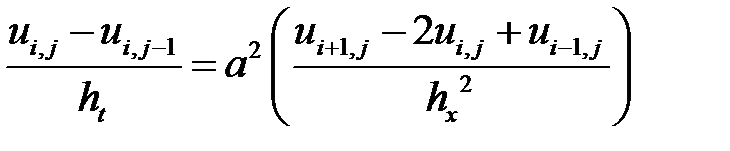 ,
, 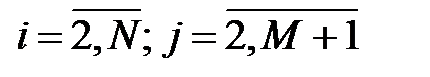 . (2. 8)
. (2. 8)
На рис. 2.2 шаблон неявной схемы показан сплошной линией.
Начальные условия записываются аналогично (2.7).
Граничные условия (2.3) на левой и правой границах задаются следующим образом: 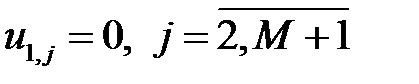 , а на правой –
, а на правой – 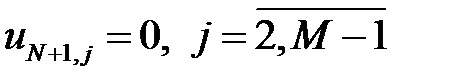 .
.
Неявная схема абсолютно устойчива, но для определения температуры в узлах на верхнем временном слое требует решения системы алгебраических уравнений. Для этого уравнение (2.8) преобразуем к виду
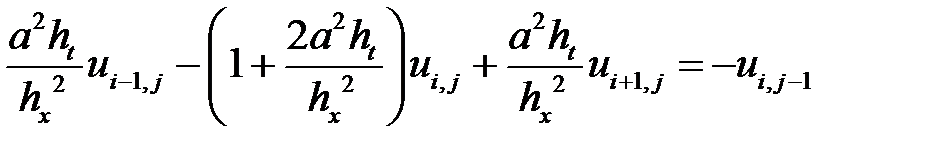 ,
, 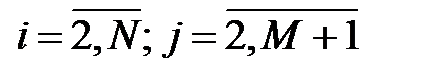 . (2.9)
. (2.9)
Полученную систему алгебраических уравнений целесообразно решать методом прогонки [7].
Система линейных алгебраических уравнений имеет вид
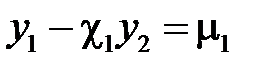
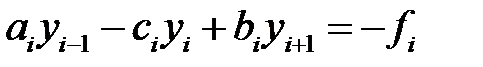 ,
, 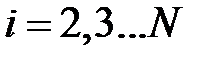
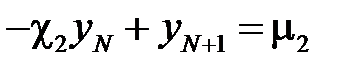
В матричной форме система уравнений запишется как
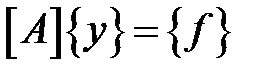
Здесь: 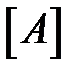 – матрица коэффициентов размерностью
– матрица коэффициентов размерностью 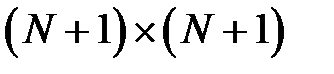 ;
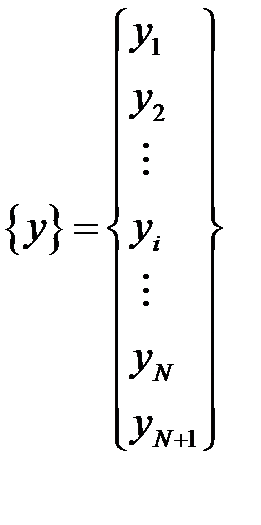
; 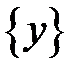 – вектор столбец неизвестных;
– вектор столбец неизвестных; 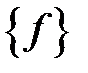 – вектор столбец свободных членов.
– вектор столбец свободных членов.
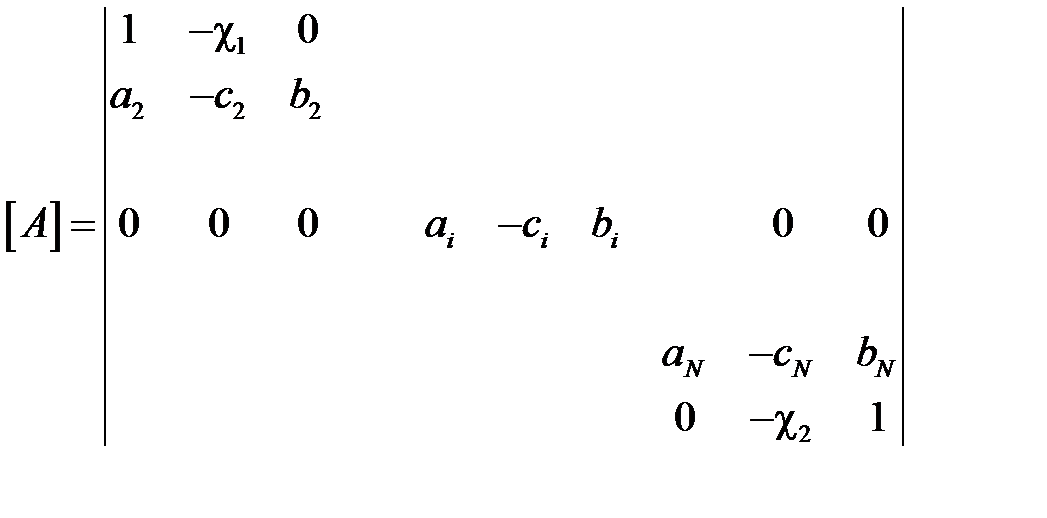 ;
;  ;
;
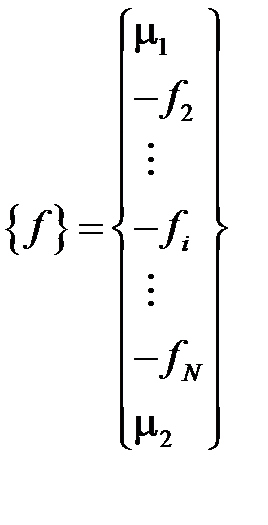 .
.
Матрица коэффициентов 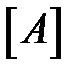 является ленточной трехдиагональной матрицей. Все ее ненулевые элементы находятся вблизи главной диагонали, т.е.
является ленточной трехдиагональной матрицей. Все ее ненулевые элементы находятся вблизи главной диагонали, т.е. 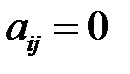 , если
, если 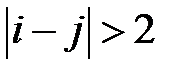 .
.
Для решения указанной системы алгебраических уравнений используем метод прогонки, являющийся разновидностью прямого метода Гаусса.
На первом этапе (прямой ход) определяются прогоночные коэффициенты:
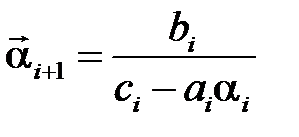 ,
, 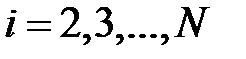
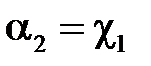
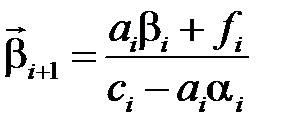 ,
, 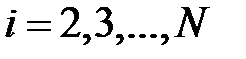
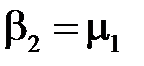
На втором этапе (обратный ход) определяются неизвестные:
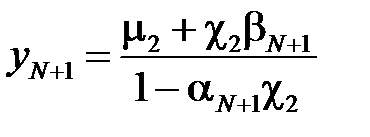
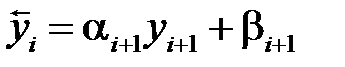 ,
, 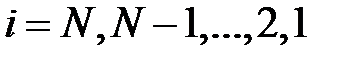
Для метода прогонки граничные условия можно задать в виде:
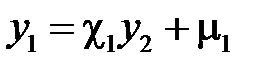 ,
, 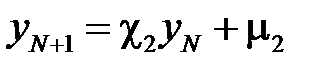
В рассматриваемой задаче на левой и правой границах заданы граничные условие первого рода. На границе задано значения функции 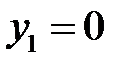 ,
, 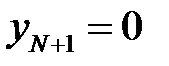 . Тогда
. Тогда 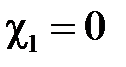 ,
, 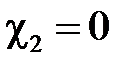 ,
, 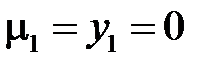 ,
, 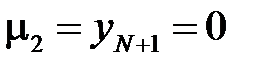 .
.
ЗАДАНИЕ
Решить уравнение параболического типа (охлаждение стержня) аналитически и методом конечных разностей (использовать неявную схему).
Конечный момент времени определить по формуле 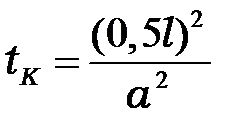 . Количество разбиений по координате
. Количество разбиений по координате 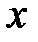 задать равным 40, а по времени
задать равным 40, а по времени 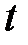 – 80. Количество членов ряда в уравнении (2.4) задать равным 50. Коэффициент теплопроводности
– 80. Количество членов ряда в уравнении (2.4) задать равным 50. Коэффициент теплопроводности 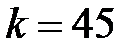 , Вт/(м2×°С); удельная теплоемкость
, Вт/(м2×°С); удельная теплоемкость 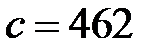 , Дж/(кг×°С); Плотность среды
, Дж/(кг×°С); Плотность среды  , кг/м3.
, кг/м3.
Варианты заданий представлены в таблице 1.1.
Таблица 1.1. Варианты заданий
| Вариант № |  , м , м
| 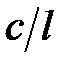 , м , м
| 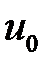 , м , м
|
| 1 | 0,10 | 0,30 | 10 |
| 2 | 0,11 | 0,35 | 11 |
| 3 | 0,12 | 0,40 | 12 |
| 4 | 0,13 | 0,45 | 13 |
| 5 | 0,14 | 0,50 | 14 |
| 6 | 0,15 | 0,55 | 15 |
| 7 | 0,16 | 0,60 | 16 |
| 8 | 0,17 | 0,65 | 17 |
| 9 | 0,18 | 0,70 | 18 |
| 10 | 0,19 | 0,65 | 19 |
| 11 | 0,20 | 0,60 | 20 |
| 12 | 0,21 | 0,55 | 21 |
Содержание отчета
1. Титульный лист.
2. Задание.
3. Постановка задачи.
4. Аналитические формулы.
5. Конечно-разностные уравнения.
6. Результаты вычислений в виде объемной картинки, полученные по аналитическим формулам и с помощью МКР.
7. Построить на одних осях графики 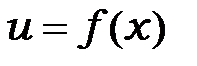 , полученные по аналитическим формулам и с помощью МКР, в моменты времени
, полученные по аналитическим формулам и с помощью МКР, в моменты времени 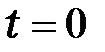 ;
; 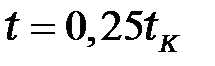 ;
; 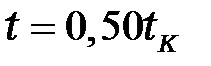 ;
; 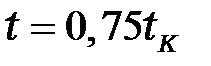 ;
; 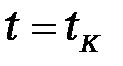 .
.
8. Найти максимальную невязку между аналитическим решением и решением МКР с указанием координаты.
9. Код программы
10. Выводы








