1. Решение уравнения гиперболического типа
Уравнения с частными производными 2-го порядка гиперболического типа наиболее часто встречаются в физических задачах, связанных с процессами колебаний. Простейшее уравнение гиперболического типа обычно называют уравнением колебаний струны. В математической физике под струной понимают гибкую, упругую нить. Натяжения, возникающие в струне в любой момент времени, направлены по касательной к ее профилю. Пусть струна длины  в начальный момент направлена по отрезку оси от 0 до
в начальный момент направлена по отрезку оси от 0 до  . Предположим, что концы струны закреплены в точках
. Предположим, что концы струны закреплены в точках 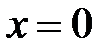 и
и 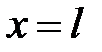 . Если струну отклонить от ее первоначального положения, а потом предоставить самой себе или, не отклоняя положение, придать в начальный момент ее точкам некоторую скорость, или отклонить струну и придать ее точкам некоторую скорость, то точки струны будут совершать движения − говорят, что струна начнет колебаться. Задача заключается в определении формы струны в любой момент времени и определении закона движения каждой точки струны в зависимости от времени.
. Если струну отклонить от ее первоначального положения, а потом предоставить самой себе или, не отклоняя положение, придать в начальный момент ее точкам некоторую скорость, или отклонить струну и придать ее точкам некоторую скорость, то точки струны будут совершать движения − говорят, что струна начнет колебаться. Задача заключается в определении формы струны в любой момент времени и определении закона движения каждой точки струны в зависимости от времени.
Будем рассматривать малые отклонения точек струны от начального положения. В силу этого можно предполагать, что движение точек струны происходит перпендикулярно оси 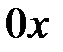 и в одной плоскости. При этом предположении процесс колебания струны описывается одной функцией
и в одной плоскости. При этом предположении процесс колебания струны описывается одной функцией 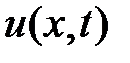 , которая дает величину перемещения точек струны с абсциссой
, которая дает величину перемещения точек струны с абсциссой 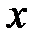 в момент
в момент 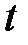 .
.
Уравнение колебаний струны (уравнение гиперболического типа) имеет вид
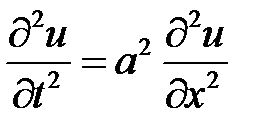 , (1.1)
, (1.1)
где 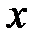 – продольная координата, м;
– продольная координата, м; 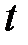 – время, с;
– время, с; 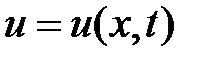 – перемещение струны, м;
– перемещение струны, м; 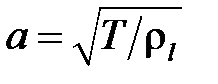 – параметр, м/с;
– параметр, м/с; 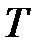 – сила натяжения (в каждой точке по координате
– сила натяжения (в каждой точке по координате 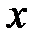
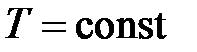 ), Н;
), Н; 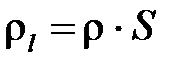 – линейная плотность струны, кг/м;
– линейная плотность струны, кг/м; 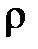 – объемная плотность струны, кг/м3;
– объемная плотность струны, кг/м3; 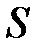 – площадь поперечного сечения, м2.
– площадь поперечного сечения, м2.
Граничные условия
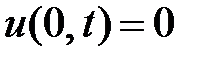 ;
; 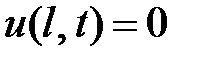 ; (1.2)
; (1.2)
Начальные условия
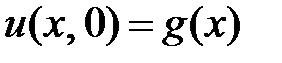 ;
; 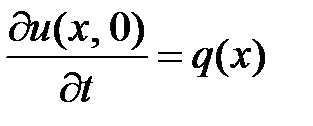 . (1.3)
. (1.3)
Решение уравнения (1.1), полученное аналитически методом разделения переменных (метод Фурье) и удовлетворяющее условиям однозначности (краевым условия) (1.2), (1.3), имеет вид
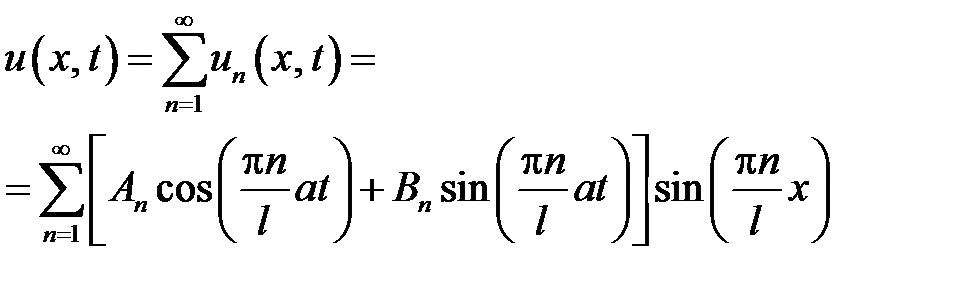 . (1.4)
. (1.4)
Здесь: 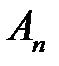 и
и 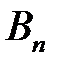 – постоянные интегрирования, определяемые из начальных условий.
– постоянные интегрирования, определяемые из начальных условий.
На рис. 1.1 показан профиль отклонения струны в нулевой момент времени. Будем считать, что начальная скорость равна нулю ( 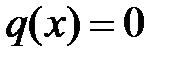 ).
).
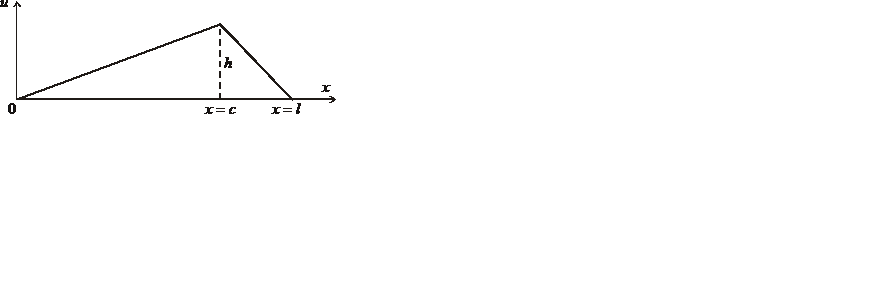
Рис. 1.1. Профиль отклонения струны в нулевой момент времени
Тогда 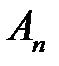 и
и 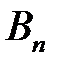 в уравнении (1.4) определяются следующим образом
в уравнении (1.4) определяются следующим образом
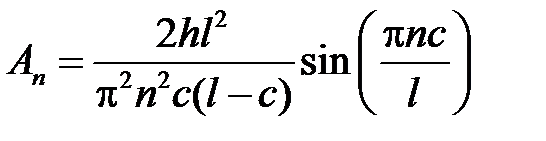 ,
, 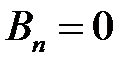 . (1.5)
. (1.5)
Решение задачи гиперболического уравнения (1.1) методом конечных разностей (МКР).
Рассмотрим решение поставленной задачи МКР по явной схеме:
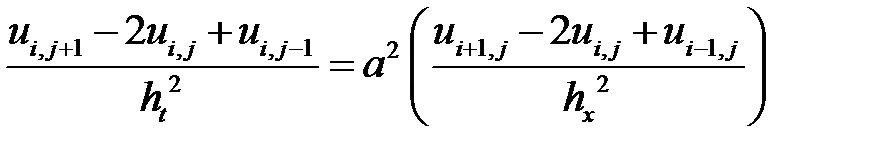 ,
, 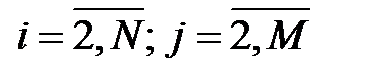 . (1.6)
. (1.6)
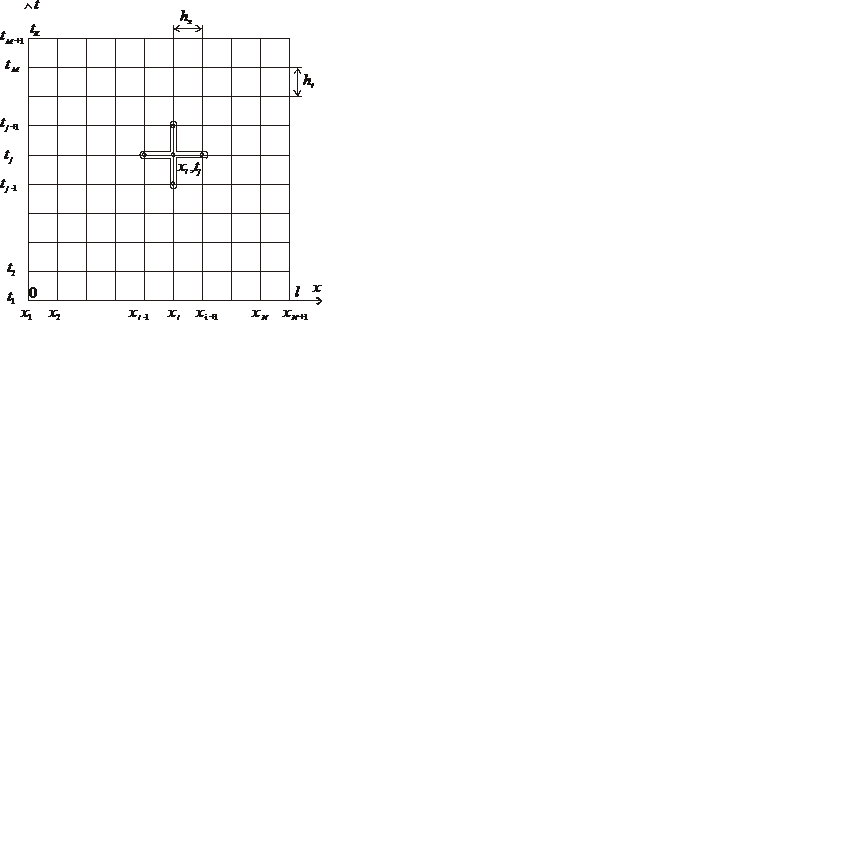
Рис. 1.2. Конечно-разностная сетка
Явная конечно-разностная схема (1.6) для волнового уравнения является устойчивой при условии
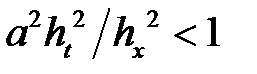 . (1.7)
. (1.7)
При решении данной задачи МКР необходимо знать значения 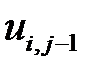 ,
, 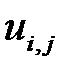 ,
, 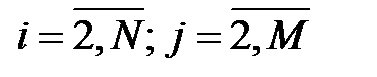 на двух предыдущих временных слоях. Для временного слоя
на двух предыдущих временных слоях. Для временного слоя 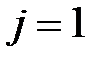 значения функции в узлах сетки определяются из начального условия
значения функции в узлах сетки определяются из начального условия
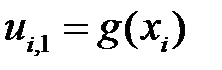 ,
, 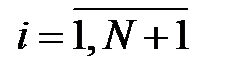 . (1.8)
. (1.8)
Для определения функции в узлах сетки для временного слоя 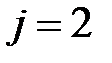 используется второе начальное условие (1.3)
используется второе начальное условие (1.3)
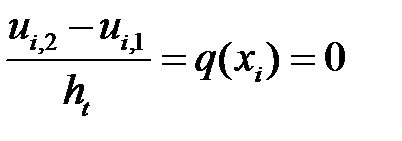 . (1.9)
. (1.9)
ЗАДАНИЕ
Решить уравнение гиперболического типа (уравнение колебания струны) аналитически и методом конечных разностей.
Конечный момент времени определить по формуле 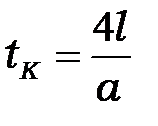 . Количество разбиений по координате
. Количество разбиений по координате 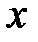 задать равным 40, а по времени
задать равным 40, а по времени 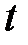 определить из выражения (1.7). Количество членов ряда в уравнении (1.4) задать равным 50
определить из выражения (1.7). Количество членов ряда в уравнении (1.4) задать равным 50
Варианты заданий представлены в таблице 1.1.
Таблица 1.1. Варианты заданий
| Вариант № |  , м , м
| 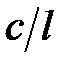 , м , м
| 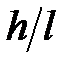 , м , м
| 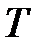 , Н , Н
| 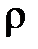 , кг/м3 , кг/м3
| 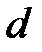 , мм , мм
|
| 1 | 0,85 | 0,30 | 0,10 | 10 | 7000 | 0,15 |
| 2 | 0,90 | 0,35 | 0,11 | 12 | 7100 | 0,16 |
| 3 | 0,95 | 0,40 | 0,12 | 14 | 7200 | 0,17 |
| 4 | 1,00 | 0,45 | 0,13 | 16 | 7300 | 0,18 |
| 5 | 1,05 | 0,50 | 0,14 | 18 | 7400 | 0,19 |
| 6 | 1,10 | 0,55 | 0,15 | 20 | 7500 | 0,20 |
| 7 | 1,15 | 0,60 | 0,16 | 22 | 7600 | 0,21 |
| 8 | 1,20 | 0,65 | 0,17 | 24 | 7700 | 0,22 |
| 9 | 1,25 | 0,70 | 0,18 | 26 | 7800 | 0,23 |
| 10 | 1,30 | 0,65 | 0,19 | 28 | 7900 | 0,24 |
| 11 | 1,35 | 0,60 | 0,20 | 30 | 8000 | 0,25 |
| 12 | 1,10 | 0,55 | 0,21 | 32 | 8100 | 0,26 |
Содержание отчета
1. Титульный лист.
2. Задание.
3. Постановка задачи.
4. Аналитические формулы.








