Сеть встречного распространения (сеть Кохонена)
В качестве меры близости двух векторов обычно выбирается евклидово расстояние:
d(x,y)=S(xi-yi).
Сеть Кохонена (T.Kohonen) состоит из одного слоя нейронов. Число входов каждого нейрона n равно размерности вектора параметров объекта. Количество нейронов совпадает с требуемым числом классов, на которые нужно разбить объекты (меняя число нейронов, можно динамически менять число классов).
Новыми прототипами становятся центроиды векторов. В качестве меры близости выступает евклидово расстояние. Сеть Кохонена обучается без учителя на основе самоорганизации. По мере обучения векторы весов нейронов становятся прототипами классов. На этапе решения информационной задачи сеть относит предъявленный объект к 1 из классов.
Для каждого j-го нейрона (j=1,2,….,m)определяет расстояние от него до входного вектора Х: 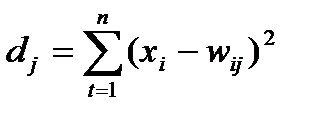
Обучение начинается с задания небольшого случайного значения весовой матрицы W. В дальнейшем: процесс самоорганизации: модификация W при предъявлении входного вектора.
Выбирается нейрон с номером k, 1£k£m, для которого это расстояние минимально. На текущем шаге обучения N будут модифицироваться только веса нейронов из окрестности нейрона k:
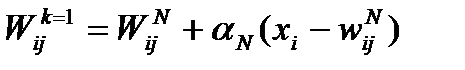
Темп обучения aN с течением времени уменьшается (a0 =0,9, aN+1 = aN -0,001).
Первоначально в окрестности любого из нейронов находятся все нейроны сети, но с каждым шагом уменьшается. В конце подстраивается под вектор весов k.
Алгоритм обучения сети Кохонена
Шаг 1. Инициализация сети. Весовым коэффициентам сети wij, i=1,2…,n, j=1,2,…,m присваиваются малые случайные значения. Задаются значения a0 —начальный темп обучения и Do — максимальное расстояние между весовыми векторами (столбцами матрицы W).
Шаг 2. Предъявление сети нового входного сигнала X.
Шаг 3. Вычисление расстояния от входа X до всех нейронов сети: 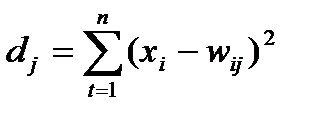
Шаг 4. Выбор нейрона k, 1£k£m с наименьшим расстоянием dk.
Шаг 5. Настройка весов нейрона k и всех нейронов, находящихся от него на расстоянии, не превосходящем DN: 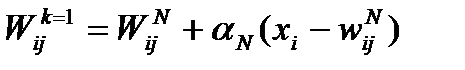
Шаг 6. Уменьшение значений aN, DN
Шаг 7. Шаги 2—6 повторяются до тех пор, пока веса не перестанут меняться (или пока суммарное изменение всех весов станет очень мало).
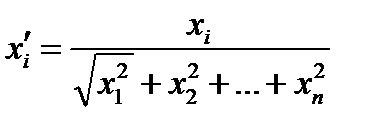
а также если после каждой итерации процесса обучения осуществлять нормировку весов каждого нейрона (столбцов матрицы W), то в качестве меры близости входных векторов и весовых векторов нейронов сети можно рассматривать скалярное произведение между ними.








