Формальная постановка задачи кластеризации
Пусть множество объектов-множество номеров (имён, меток) кластеров. Задана функция расстояния между объектами. Имеется конечная обучающая выборка объектов. Требуется разбить выборку на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из объектов, близких по метрике, а объекты разных кластеров существенно отличались. При этом каждому объекту приписывается номер кластера. Алгоритм кластеризации— это функция, которая любому объекту ставит в соответствие номер кластера. Множество в некоторых случаях известно заранее, однако чаще ставится задача определить оптимальное число кластеров, с точки зрения того или иного критерия качества кластеризации. Кластеризация (обучение без учителя) отличается от классификации (обучения с учителем) тем, что метки исходных объектов изначально не заданы, и даже может быть неизвестно само множество.
Решение задачи кластеризации принципиально неоднозначно, и тому есть несколько причин:
· не существует однозначно наилучшего критерия качества кластеризации. Известен целый ряд эвристических критериев, а также ряд алгоритмов, не имеющих чётко выраженного критерия, но осуществляющих достаточно разумную кластеризацию «по построению». Все они могут давать разные результаты. Следовательно, для определения качества кластеризации требуется эксперт предметной области, который бы мог оценить осмысленность выделения кластеров.
· число кластеров, как правило, неизвестно заранее и устанавливается в соответствии с некоторым субъективным критерием. Это справедливо только для методов дискриминации, так как в методах кластеризации выделение кластеров идёт за счёт формализованного подхода на основе мер близости.
· результат кластеризации существенно зависит от метрики, выбор которой, как правило, также субъективен и определяется экспертом. Но стоит отметить, что есть ряд рекомендаций к выбору мер близости для различных задач.
Методы кластеризации:
· иерархические
· неиерархические
Суть иерархической кластеризации состоит в последовательном объединении меньших кластеров в большие или разделении больших кластеров на меньшие.
Иерархические методы могут быть агломеративными (объединительными) и дивизивными. Агломеративная кластеризация начинается с каждого объекта в отдельном кластере. Кластеры объединяют, группируя объекты каждый раз во все более и более крупные кластеры. Этот процесс продолжают до тех пор, пока все объекты не станут членами одного единственного кластера.
Разделяющая, или дивизивная, кластеризация начинается со всех объектов, сгруппированных в единственном кластере. Кластеры делят (расщепляют) до тех пор, пока каждый объект не окажется в отдельном кластере.
Обычно в маркетинговых исследованиях используют агломеративные методы, например, методы связи, дисперсионные и центроидные методы. Методы связи включают метод одиночной связи, метод полной связи и метод средней связи.
В основе метода одиночной связи лежит минимальное расстояние, или правило ближайшего соседа. При формировании кластера первыми объединяют два объекта, расстояние между которыми минимально. Далее определяют следующее по величине самое короткое расстояние, и в кластер с первыми двумя объектами вводят третий объект. На каждой стадии расстояние между двумя кластерами представляет собой расстояние между их ближайшими точками.
Метод полной связи аналогичен методу одиночной связи, за исключением того, что в его основе лежит максимальное расстояние между объектами, или правило дальнего соседа. В методе полной связи расстояние между двумя кластерами вычисляют как расстояние между двумя их самыми удаленными точками.
Метод средней связи действует аналогично. Однако в этом методе расстояние между двумя кластерами определяется как среднее значение всех расстояний, измеренных между объектами двух кластеров, при этом в каждую пару входят объекты из разных кластеров.
Широко известным дисперсионным методом является Метод Варда. Дисперсионный метод, в котором кластеры формируют таким образом, чтобы минимизировать квадраты евклидовых расстояний до кластерных средних. Для каждого кластера вычисляют средние всех переменных. Затем для каждого объекта вычисляют квадраты евклидовых расстояний до кластерных средних. Эти квадраты расстояний суммируют для всех объектов. На каждой стадии объединяют два кластера с наименьшим приростом в полной внутрикластерной дисперсии.
В центроидных методах расстояние между двумя кластерами представляет собой расстояние между их центроидами (средними для всех переменных). Каждый раз объекты группируют и вычисляют новый центроид. Изо всех иерархических методов методы средней связи и Варда показывают наилучшие результаты по сравнению с другими методами.
Иерархические методы кластерного анализа используются при небольших объемах наборов данных. Иерархические алгоритмы связаны с построением дендрограмм (от греческого dendron - "дерево"), которые являются результатом иерархического кластерного анализа. Дендрограмма описывает близость отдельных точек и кластеров друг к другу, представляет в графическом виде последовательность объединения (разделения) кластеров.
Дендрограмма (dendrogram) - древовидная диаграмма, содержащая n уровней, каждый из которых соответствует одному из шагов процесса последовательного укрупнения кластеров.
Существует много способов построения дендограмм. В дендограмме объекты могут располагаться вертикально или горизонтально. Пример вертикальной дендрограммы приведен на рис 3.
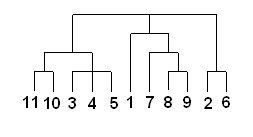
Рис. 3 Пример дендрограммы
Числа 11, 10, 3 и т.д. соответствуют номерам объектов или наблюдений исходной выборки. Мы видим, что на первом шаге каждое наблюдение представляет один кластер (вертикальная линия), на втором шаге наблюдаем объединение таких наблюдений: 11 и 10; 3, 4 и 5; 8 и 9; 2 и 6. На втором шаге продолжается объединение в кластеры: наблюдения 11, 10, 3, 4, 5 и 7, 8, 9. Данный процесс продолжается до тех пор, пока все наблюдения не объединятся в один кластер.
К другому типу процедур кластеризации относятся неиерархические методы кластеризации. К данному типу относят, например, метод k-средних. Этот метод включает последовательный пороговый метод, параллельный пороговый метод и оптимизирующее распределение. В последовательном пороговом методе выбирают центр кластера и все объекты, находящиеся в пределах заданного от центра порогового значения, группируют вместе. Затем выбирают новый кластерный центр, и процесс повторяют для не сгруппированных точек. После того как объект помещен в кластер с этим новым центром, его уже не рассматривают как объект для дальнейшей кластеризации.
К этому же типу кластеризации относят самоорганизующиеся карты Кохонена. Сети, называемые картами Кохонена, - это одна из разновидностей нейронных сетей, однако они принципиально отличаются от рассмотренных выше методов, поскольку используют неконтролируемое обучение. При таком обучении обучающее множество состоит лишь из значений входных переменных, в процессе обучения нет сравнивания выходов нейронов с эталонными значениями. Можно сказать, что такая сеть учится понимать структуру данных. Самоорганизующиеся карты могут использоваться для решения таких задач, как моделирование, прогнозирование, поиск закономерностей в больших массивах данных, выявление наборов независимых признаков и сжатие информации.
В результате обучения карта Кохонена классифицирует входные примеры на кластеры (группы схожих примеров) и визуально отображает многомерные входные данные на плоскости нейронов. Уникальность метода самоорганизующихся карт состоит в преобразовании n-мерного пространства в двухмерное.
Неиерархические методы выявляют более высокую устойчивость по отношению к шумам и выбросам, некорректному выбору метрики, включению незначимых переменных в набор, участвующий в кластеризации. Ценой, которую приходится платить за эти достоинства метода, является слово "априори". Аналитик должен заранее определить количество кластеров, количество итераций или правило остановки, а также некоторые другие параметры кластеризации. Это сложно начинающим специалистам.
Если нет предположений относительно числа кластеров, рекомендуют использовать иерархические алгоритмы кластерного анализа. Однако если объем выборки не позволяет это сделать, возможный путь - проведение ряда экспериментов с различным количеством кластеров, например, начать разбиение совокупности данных с двух групп и, постепенно увеличивая их количество, сравнивать результаты. За счет такого "варьирования" результатов достигается достаточно большая гибкость кластеризации.
Иерархические методы, в отличие от неиерархических, отказываются от определения числа кластеров, а строят полное дерево вложенных кластеров. Сложности иерархических методов кластеризации: ограничение объема набора данных; выбор меры близости; негибкость полученных классификаций. Преимущество этой группы методов в сравнении с неиерархическими методами - возможность получить детальное представление о структуре данных.
Неиерархическая кластеризация быстрее иерархических методов, и ее выгодно использовать при большом числе объектов или наблюдений.
Кластерный анализ является очень удобным средством для выделения сегментов рынка, особенно в наш век высоких технологий, когда на помощь человеку приходят машины, и столь трудоемкий процесс становиться буквально секундным делом.
2.2 Нейронной сети. Сеть Кохонена
Однослойные искусственные нейронные сети
Рис.4. Однослойная нейронная сеть Y=XW.
Нейронная сеть состоит из множества одинаковых элементов – нейронов. Нейрон моделируется как устройство, имеющее несколько входов (дендриты) и 1 выход (аксион). Каждому выходу ставится в соответствие некоторый весовой коэффициент 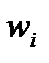 .
.
Внутри самого нейрона происходит взвешенное суммирование входных сигналов. Получаемые значение являются аргументом оптимизационной функции нейрона.
Простейшая нейронная сеть состоит из групп нейронов, которые образуют некоторый слой. Удобно считать веса w элементами некоторой матрицы w, которая имеет m строк и n столбцов. Т.о. выходом нейронной сети будет вектор y=w*x, где х – вектор входов, w – матрица, указывающая на возможные соединения.
Многослойные искусственные нейронные сети
Рис. 5. Многослойная нейронная сеть
Многослойная нейронная сеть: более крупные и сложные нейронные сети обладают и более мощными вычислительными возможностями. Нейрон передает свой выходной сигнал всем остальным, включая себя, копирует слоистые структуры мозга человека.
Многослойные сети могут привести к увеличению вычислительной мощности по отношению к однослойным сетям.
Вычисления выходного слоя заключаются в умножении входного вектора на первую весовую матрицу. Т.к. умножение матриц ассоциативно, то (в частности) двуслойная нейросеть будет эквивалентна однослойной. Любую многослойную сеть можно заменить эквивалентной однослойной, если функции линейны.
Будучи соединенными определенные обработанные нейроны обрабатывают нейронную сеть. Работа сети разделяется на обучение и адаптацию.
Обучение – процесс адаптации сети, предъявляемый эталонным образом путем модификации весовых коэффициентов между нейронами.
Основным преимуществом нейронных сетей является возможность выразить зависимость входа/выхода на этапе обучения без предварительной аналитической работы.
Недостатком нейронных сетей является то, что невозможно объяснить выходной результат.
Обучение искусственных нейронных сетей
Обучение. Чтобы для некоторого множества входов получить некоторые выходы, в процессе обучения веса становятся такими, чтобы каждый входной вектор вырабатывал нужный выходной вектор.
Обучение с учителем – аналог обучения нейронных сетей.
Обучение с учителем предполагает, что для каждого входного вектора существует целевой вектор, представляющий собой требуемый выход. Эти 2 вектора – обучающая пара. Векторы предъявляются последовательно, пока ошибка не будет на допустимо низком уровне.
Обучение без учителя. Не нуждается в целевом векторе и, следовательно, не требует сравнения с предопределяемыми идеальными ответами. Подстраивает веса в сети так, чтобы получились согласованные выходные векторы, т.е., чтобы при предъявлении достаточно близких входных векторов, система давала правильные ответы. Процесс обучения выделяет некоторые свойства обучающего множества и загружает векторы в классы. Если на вход предъявили вектор из данного класса, это даст определенный выходной вектор. Но до обучения невозможно предсказать, какой вектор будет производиться данным классом входных векторов.
Алгоритм обучения – такой набор формул, позволяющий по вектору ошибки вычислять требуемые поправки для весов сети.
Если выбрано множество примеров и способов вычисления ошибки, то обучение нейронной сети превращается в задачу многомерной оптимизации (имеющую большую размерность). Для решения этой задачи используются следующие алгоритмы:
1) Алгоритм локальной оптимизации с вычислением частных производных 1-го порядка
2) Алгоритмы локальной оптимизации с вычислением частичных производных 1-го и 2-го порядка (м-д Ньютона, м-д Гаусса и др.)
3) Стохастические методы оптимизации (м-д Монте Карло, поезд в случае направлении и т.д.)
4) Алгоритмы глобальной оптимизации (решается с помощью перебора значений переменных)
Классификация нейронных сетей и их свойства.
Как правило передаточные функции всех нейронов фиксированы, а веса являются параметрами сети и могут изменяться.
Подавая числа на входы сети, получаем некоторый набор чисел на выходах сети. В общем следующая работа сети состоит в преображении входящего потока х в выходящий вектор у; это преображение задается весами сети.
Считается, что практически любую задачу распознания можно свести к задаче, решаемой нейронной сетью.
В зависимости от функций, выполненных нейронами сети, можно выделить 3 их этапа:
1. Входные нейроны (те, на которые подается входящий вектор или входящий сигнал, кодирующий образ внешней среды). Во входящем нейроне обычно никаких вычислений не происходит, просто информация передается со входа на выход, путем изменения его активации.








