1 метод. По определению логарифма.
Так решаются простейшие уравнения вида 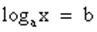 .
.
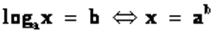
Решить уравнение : 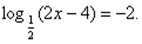
Как вы предлагаете его решать? (По определению логарифма).Решение. 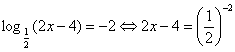 , Отсюда 2х – 4 = 4; х = 4.
, Отсюда 2х – 4 = 4; х = 4.
Ответ: 4.
В этом задании 2х – 4 > 0, так как 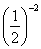 > 0, поэтому посторонних корней появиться не может, и проверку нет необходимости делать. Условие 2х – 4 > 0 в этом задании выписывать не надо.
> 0, поэтому посторонних корней появиться не может, и проверку нет необходимости делать. Условие 2х – 4 > 0 в этом задании выписывать не надо.
2 метод. Потенцирование (переход от логарифма данного выражения к самому этому выражению).
Рассмотрим пример : 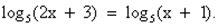
Какую особенность вы заметили? (Основания одинаковы и логарифмы двух выражений равны). Что можно сделать? (Потенцировать).
При этом надо учитывать, что любое решение содержится среди всех х, для которых логарифмируемые выражение положительны.
Решение 1. ОДЗ: 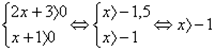
Потенцируем исходное уравнение 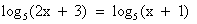 , получим уравнение 2x + 3 = х + 1.
, получим уравнение 2x + 3 = х + 1.
Решаем его: х = -2. Это решение не подходит ОДЗ, значит, данное уравнение корней не имеет.
Можно решить это уравнение иначе – переходом к равносильной системе:
Уравнение 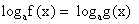
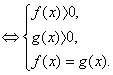
(Система содержит избыточное условие – одно из неравенств можно не рассматривать).
Решение 2. Уравнение 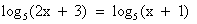 равносильно системе:
равносильно системе:
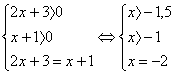
Эта система решений не имеет.
Есть еще один вариант решения – переход к следствию из данного уравнения. При неравносильных преобразованиях найденное решение необходимо проверить подстановкой в исходное уравнение.
Решение 3. 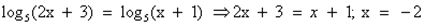 .
.
Сделаем проверку: 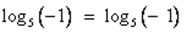 неверно, так как не имеет смысла.
неверно, так как не имеет смысла.
Ответ: корней нет.
Вопрос Какое из этих трех решений вам больше всего понравилось? Вы имеете право решать любым способом.
3. Введение новой переменной.
Рассмотрим пример. 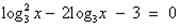 .
.
Что вы заметили? (Это квадратное уравнение относительно log3x).
Ваши предложения? (Ввести новую переменную)
Решение. ОДЗ: х > 0.
Пусть 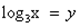 , тогда уравнение примет вид:
, тогда уравнение примет вид: 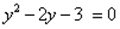 . Дискриминант D > 0. Корни по теореме Виета:
. Дискриминант D > 0. Корни по теореме Виета: 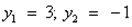 .
.
Вернемся к замене: 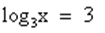 или
или 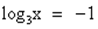 .
.
Решив простейшие логарифмические уравнения, получим:
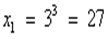 ;
; 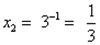 . Ответ: 27;
. Ответ: 27; 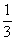
4. Логарифмирование обеих частей уравнения.
Решить уравнение: 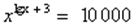 .
.
Решение: ОДЗ: х>0, прологарифмируем обе части уравнения по основанию 10: 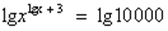
Применим свойство логарифма степени:
(lgx + 3) lgx = 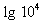
(lgx + 3) lgx = 4
Пусть lgx = y, тогда (у + 3)у = 4
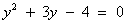 , (D > 0) корни по теореме Виета: у1 = -4 и у2 = 1.
, (D > 0) корни по теореме Виета: у1 = -4 и у2 = 1.
Вернемся к замене, получим: lgx = -4, 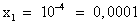 ; lgx = 1,
; lgx = 1, 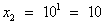 .
.
Ответ: 0,0001; 10.
5. Приведение к одному основанию.
Решите уравнение: 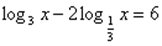
Решение: ОДЗ: х>0. Перейдем к основанию 3.
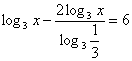 или
или 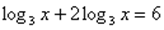 ;
; 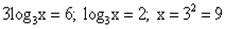 .
.
Ответ: 9. 6. Функционально-графический метод. Решить графически уравнение: 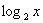 = 3 – x.
= 3 – x.
Как вы предлагаете решать?
(Строить по точкам графики двух функций у = log2x и y = 3 – x и искать абсциссу точек пересечения графиков). 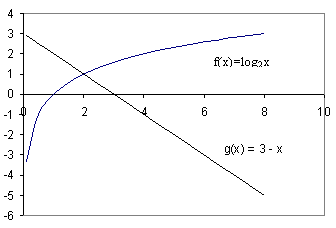
Есть способ, позволяющий не строить графики. Он заключается в следующем: если одна из функций у = f(x) возрастает, а другая y = g(x) убывает на промежутке Х, то уравнение f(x)= g(x) имеет не более одного корня на промежутке Х. Если корень имеется, то его можно угадать. В нашем случае функция 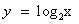 возрастает при х>0, а функция y = 3 – x убывает при всех значениях х, в том числе и при х>0, значит, уравнение
возрастает при х>0, а функция y = 3 – x убывает при всех значениях х, в том числе и при х>0, значит, уравнение 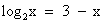 имеет не более одного корня. Заметим, что при х = 2 уравнение обращается в верное равенство, так как
имеет не более одного корня. Заметим, что при х = 2 уравнение обращается в верное равенство, так как 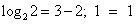 . Ответ: 2.
. Ответ: 2.
6. Первичное закрепление. «Правильному применению методов можно научиться,
только применяя их на различных примерах».
(Датский историк математики Г. Г. Цейтен)
Предложите метод решения уравнений: 1) 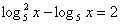 2)
2) 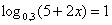
3) 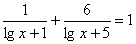 4)
4) 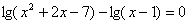 5)
5) 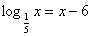
6) 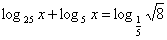
7. Информация о домашнем задании. Выуч. П. 19
№337(2), №338(2), №339(2), №340(2), №341(2).
«Что есть больше всего на свете?
Пространство.
Что мудрее всего?
Время.
Что приятнее всего?
Достичь желаемого».
Фалес
Желаю всем достичь желаемого.








