Тема: Логарифмические уравнения.
16.02.22.г. Алгебра 10 класс
Аудиторное занятие №44
Тема: Логарифмические уравнения.
Цели урока:
- образовательная: формирование знаний о разных способах решения логарифмических уравнений, умений применять их в каждой конкретной ситуации и выбирать для решения любой способ;
- развивающая: развитие умений наблюдать, сравнивать, применять знания в новой ситуации, выявлять закономерности, обобщать; формирование навыков взаимоконтроля и самоконтроля;
- воспитательная: воспитание ответственного отношения к учебному труду, внимательного восприятия материала на уроке, аккуратности ведения записей.
«Изобретение логарифмов, сократив работу астронома, продлило ему жизнь». (французский математик, астроном П.С. Лаплас)
Изученные определение логарифма, свойства логарифмов и логарифмической функции позволят нам решать логарифмические уравнения. Все логарифмические уравнения, какой бы сложности они не были, решаются по единым алгоритмам. Эти алгоритмы рассмотрим сегодня на уроке. Их немного. Если их освоить, то любое уравнение с логарифмами будет посильно каждому из вас.
Повторим: 1) При каких значениях х имеет смысл функция:
а) 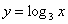 б)
б) 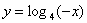 в)
в) 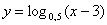 г)
г) 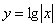
2) Совпадают ли графики функций? а) y = x и 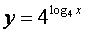 б)
б) 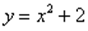 и
и 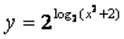
3) Перепишите равенства в виде логарифмических равенств:
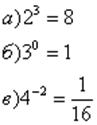
4) Запишите числа в виде логарифмов с основанием 2:
4 = - 2 = 0,5 = 1 =
5) Вычислите: 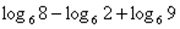
.
«Уравнение – это золотой ключ, открывающий все математические сезамы».
Современный польский математик С. Коваль.
Попробуйте сформулировать определение логарифмического уравнения. (Уравнение, содержащее неизвестное под знаком логарифма).
Рассмотрим простейшее логарифмическое уравнение: log аx = b
(где а>0, a ≠ 1 ). Так как логарифмическая функция возрастает (или убывает) на множестве положительных чисел и принимает все действительные значения, то по теореме о корне следует, что для любого b данное уравнение имеет, и притом только одно, решение, причем положительное.
Вспомните определение логарифма. (Логарифм числа х по основанию а – это показатель степени, в которую надо возвести основание а, чтобы получить число х). Из определения логарифма сразу следует, что а b является таким решением. Методы решения логарифмов.








