3 °. Вертикальных асимптот нет, так как функция определена при всех действительных значениях х.
Инструкционная карта
практического занятия № 9
по учебной дисциплине ЕН.01 Математика
Специальности:
13.02.11 Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (горная отрасль)
19.02.10Технология продукции общественного питания
Тема занятия: «Исследование функций с помощью производной и построение графиков»
Цели занятия:
Дидактическая: Отработать навыки решения задач на построение графиков функций с использованием производной.
Воспитательная: Решение прикладных задач имеет большое значение, так как позволяет ознакомить студентов с математическим моделированием как методом научного познания окружающего нас мира, различать то или иное математическое понятие в разных жизненных ситуациях.
Дисциплинарная интеграция: физика, техническая механика.
Методическое обеспечение: опорные конспекты по данной теме, задания для индивидуальной работы.
Примерное алгоритм решение задач:
Пример 1. Исследовать функцию 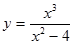 и построить ее график.
и построить ее график.
Решение.
1. Функция определена при любом действительном значении аргумента 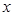 за исключением
за исключением 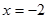 и
и 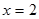 . Итак, область определения данной функции
. Итак, область определения данной функции 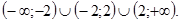
2. Так как  , то данная функция нечетная и ее график симметричен началу координат. На этом основании можно ограничиться исследованием и построением графика только для
, то данная функция нечетная и ее график симметричен началу координат. На этом основании можно ограничиться исследованием и построением графика только для 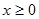 . Вторая часть графика (для
. Вторая часть графика (для 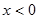 ) может быть достроена по симметрии.
) может быть достроена по симметрии.
Функция не периодическая.
3. Найдем точки пересечения с осями координат 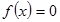 . Уравнение
. Уравнение 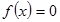 имеет единственное решение, то есть график функции проходит через начало координат
имеет единственное решение, то есть график функции проходит через начало координат 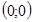 . Других точек пересечения графика функции с осями координат нет.
. Других точек пересечения графика функции с осями координат нет.
4. Вертикальные асимптоты могут пересекать ось абсцисс в точках 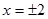 . Поскольку пределы функции при = 2-0 (слева) и при = 2+0 (справа) бесконечные, то есть.
. Поскольку пределы функции при = 2-0 (слева) и при = 2+0 (справа) бесконечные, то есть. 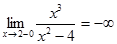 и
и 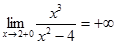 , то прямая
, то прямая 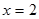 есть вертикальная асимптота. В силу симметрии графика
есть вертикальная асимптота. В силу симметрии графика 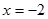 также вертикальная асимптота.
также вертикальная асимптота.
5. Поведение функции на бесконечности: 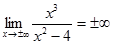 .
.
Следовательно, горизонтальных асимптот функция не имеет. Найдем наклонные асимптоты 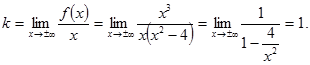
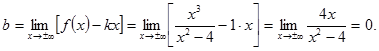
Подставим 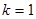 и
и 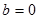 в уравнение прямой
в уравнение прямой 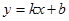 . Таким образом, наклонная асимптота графика функции имеет вид
. Таким образом, наклонная асимптота графика функции имеет вид 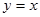 .
.
6. Интервалы монотонности и экстремумы. Найдем производную функции: 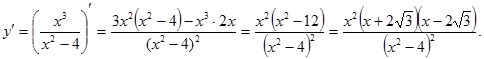
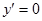 при,
при, 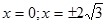 и
и 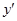 и не существует при
и не существует при 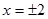 .
.
Однако критическими являются только точки 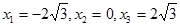 (поскольку значения
(поскольку значения 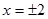 не входят в область определения функции).
не входят в область определения функции).
Исследуем на экстремум только в точку 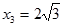 (точки
(точки 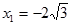 и
и 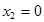 на экстремум не исследуем, так как при симметричной достройке графика вопросы о экстремум в этих точках будет решен без использования достаточного условия).
на экстремум не исследуем, так как при симметричной достройке графика вопросы о экстремум в этих точках будет решен без использования достаточного условия).
Рассмотрим знаки 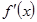 в интервалах
в интервалах 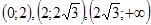 и составим таблицу:
и составим таблицу:
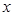
| 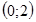
| 2 | 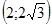
| 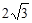
| 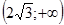
|
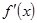
| - | Не существует | - | 0 | + |
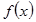
| 
| Не существует | 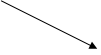
| min
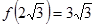
| 
|
Из таблицы получается, что функция убывает при 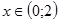 и
и 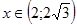 , а возрастает при
, а возрастает при 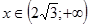 .
.
Точка - 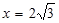 точка минимума
точка минимума 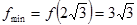 и минимум функции.
и минимум функции.
7. Интервалы выпуклости и точки перегиба.
Найдем вторую производную 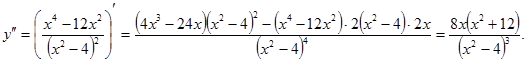
Вторая производная преобразуется в ноль при 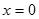 и не существует при
и не существует при 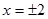 , но точки
, но точки 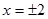 не принадлежат области определения.
не принадлежат области определения.
Рассмотрим знаки второй производной на интервалах 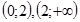 . При
. При 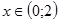
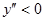 график функции на этом интервале выпуклый вверх. При
график функции на этом интервале выпуклый вверх. При 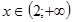
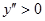 график функции на этом интервале выпуклый вниз. Точка
график функции на этом интервале выпуклый вниз. Точка 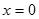 - точка перегиба функции в силу симметрии относительно начала координат.
- точка перегиба функции в силу симметрии относительно начала координат.
7. Построим график функции для  и симметрично отразим его относительно начала координат (рис. 1).
и симметрично отразим его относительно начала координат (рис. 1).
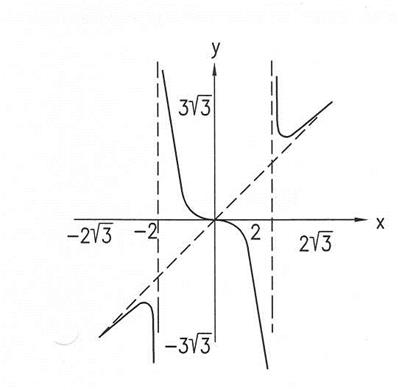
Рис. 1.
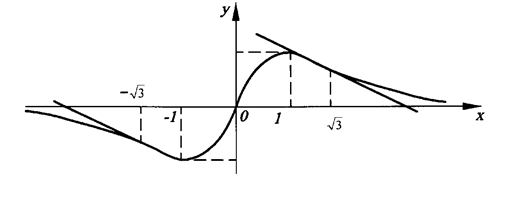
Пример 2. Исследовать функцию 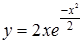 и построить ее график.
и построить ее график.
Решение.
1 °. Область определения (- ∞, + ∞).
2 °. Функция нечетная, так как f (-x) = - f (x) и ее график симметричен относительно начала координат.
3 °. Вертикальных асимптот нет, так как функция определена при всех действительных значениях х.
4 °. Поведение функции на бесконечности: 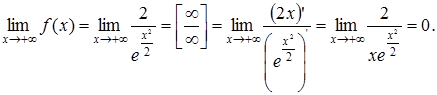
В силу нечетности функции 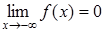 , то есть прямая у = 0 (ось абсцисс) - горизонтальная асимптота.
, то есть прямая у = 0 (ось абсцисс) - горизонтальная асимптота.
5 °. Экстремумы и интервалы монотонности: 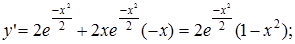
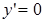 при х =
при х =  1,
1,
то есть критические точки 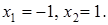
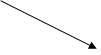
Знаки производной изображены на рис. 2.
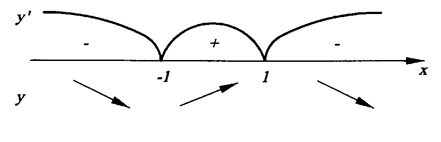
Таким образом, 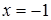 есть точка минимума; х = 1 - точка максимума и
есть точка минимума; х = 1 - точка максимума и 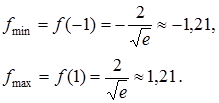
Функция убывает на интервалах (- ∞, -1) і (-1, + ∞) и возрастает на интервале (-1;1).
6 °. Интервалы выпуклости и точки перегиба:
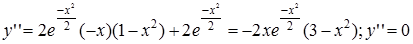 при х = 0 і
при х = 0 і 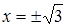 .
.
Знаки второй походной изображены на рис. 3.
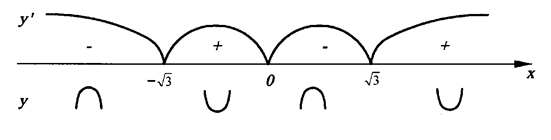
Таким образом, функция выпуклая вниз на интервалах 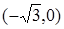 и
и 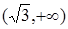 и выпуклая вверх на интервалах
и выпуклая вверх на интервалах 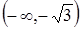 і
і 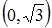 , а
, а 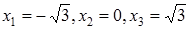 , а - точки перегиба.
, а - точки перегиба.
7. f (0)=0. Уравнение f (x)=0 имеет единственное решение x = 0, то есть график функции пересекает оси в начале координат (0; 0).
График функции изображен на рис.5 .
Задания для самостоятельной работы
Выполнить полное исследование функций и построить график.
1. 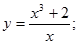 9.
9. 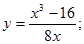 17.
17. 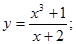 25.
25. 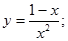
2. 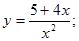 10.
10. 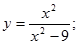 18.
18. 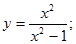 26.
26. 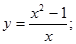
3. 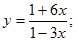 11.
11. 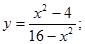 19.
19. 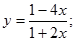 27.
27. 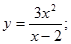
4. 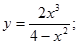 12.
12. 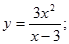 20.
20. 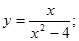 28.
28. 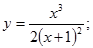
5. 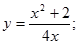 13.
13. 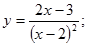 21.
21. 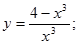 29.
29. 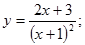
6. 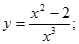 14.
14. 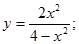 22.
22. 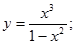 30.
30. 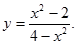
7. 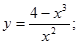 15.
15. 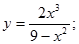 23.
23. 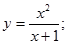
8. 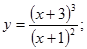 16.
16. 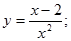 24.
24. 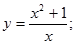
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Интервалы монотонности и экстремумы функции.
2. Интервалы выпуклости и точки перегиба.
3. Поведение функции в бесконечности.
ЛИТЕРАТУРА.
1. В.В. Пак, Ю.Л. Носенко “Высшая математика” Д.: Сталкер, !997, с. 181-193.
2.В. А. Кудрявцев, В. П. Демидович «Краткий курс высшей математики!» Наука, 1975, гл. XIII.
3. Ю. М. Почтман Основы математики: учебно-методическое пособие”, М.: МАУП, 1999, с. 57-52.
4. «Курс математики для техникумов ч. 2», ред. Н. М. Матвеева, М.: Наука, 1976, с. 9-14.








