Последовательность решения задачи
Примеры решения задач.
ОПРЕДЕЛЕНИЕ РЕАКЦИИ СВЯЗЕЙ ГРАФИЧЕСКИ.
Груз F =1000 Н удерживается с помощью двух невесомых стержней, шарнирно скрепленных между собой в точке A и в шарнирах B и C с вертикальной стеной (α=60o, β=30o).
Определить усилия в стержнях AB и BC
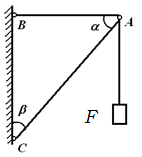
В данном случае следует рассмотреть равновесие точки A, т.к. все силы приложены в этой точке.
Нить с грузом натянута силой F. В равновесии точку A удерживают два невесомых стержня. Их реакции всегда направлены вдоль стержней.
Реакции принято направлять от узла (точки A), т.е. предполагается, что стержни работают на растяжение . В случае отрицательного ответа при решении уравнений стержень работает на сжатие.
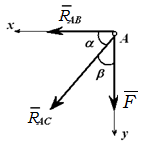
При равновесии системы сил выполняется равенство F + RAB + RAC =0
Это векторное равенство можно построить. Откладываем в масштабе известную силу F, к концу вектора прибавляем R AB, т.к. его величина и направление неизвестны, проводим через конец вектора F горизонтальную линию (параллельно R AB).
Замыкающий вектор R AC должен пройти через начало вектора F под углом β к вертикали.
Результатом построения является замкнутый треугольник
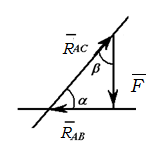
Величины усилий в стержнях можно получить, умножая замеренные значения векторов сил на масштаб или воспользовавшись теоремой синусов:
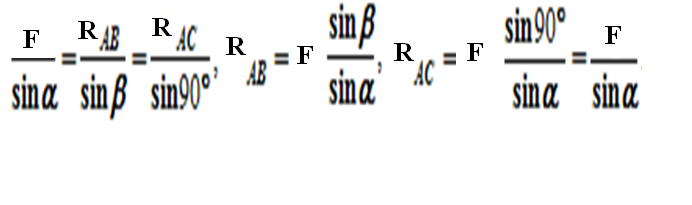
Направление силы RAC в силовом треугольнике говорит о том,
что этот стержень работает на сжатие.
ОПРЕДЕЛЕНИЕ ОПОРНЫХ РЕАКЦИЙ БАЛКИ
Последовательность решения задачи
1. Балку освободить от связей (связи) и их (его) действие заменить силами реакций.
2. Выбрать координатные оси.
3. Составить и решить уравнения равновесия.
Реакции опор можно определить, исходя из трех форм уравнений равновесия:
| а) | å F i х = 0; å F i у = 0 ; å МА = 0; | б) | å F i х = 0; å МА = 0; å МВ = 0; | в) | å МА = 0; å МВ = 0; å МС = 0. |
4. Проверить правильность решения задачи. Проверку необходимо производить по тому уравнению равновесия, которое не было использовано при решении данной задачи (задача решена правильно лишь в том случае, если после постановки значений активных и реактивных сил в уравнение равновесия выполняется условие равновесия).
5. Сделать анализ решенной задачи (если при решении задачи реакции опор или реактивный момент получается отрицательным, то их действительное направление противоположно принятому).
Пример 1. Определить реакции опор балки, если известно
F = 20 кН , М =10 кН × м, q = 1 кН/м (рис. 1).
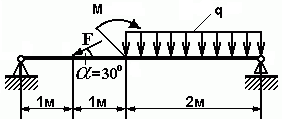
Рис. 1 - Схема задачи
Решение:
1. Изображаем балку вместе с нагрузками.
2. Выбираем расположение координатных осей, совместив ось Х с балкой, а ось У направив перпендикулярно оси Х.
3. Производим необходимые преобразования заданных активных сил: силу, накопленную к оси балки под углом α, заменяем двумя взаимно перпендикулярными составляющими
F х = F × с os 30 ° = 20 × 0,866 = 17, 32 кН
F у = F × с os 60 ° = 20 × 0,5 = 10 кН,
а равномерно распределенную нагрузку - её равнодействующей
Q = q × CD = 1 × 2 = 2 кН,
Равнодействующая Q приложена в середине участка CD, в точке К (рис. 2).
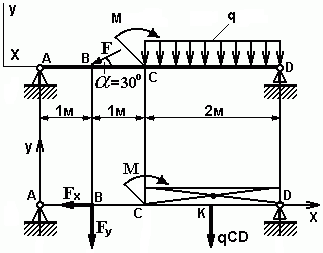
Рис. 2 - Схема преобразования заданных активных сил
4.Освобождаем балку от опор, заменив их опорными реакциями, направленными вдоль выбранных осей координат (рис 3).
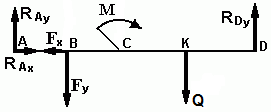
Рис. 3 - Схема реакций балки
5.Составляем уравнения равновесия статики для произвольной плоской системы сил таким образом и в такой последовательности, чтобы решением каждого из этих уравнений было определение одной из неизвестных реакций опор и определяем неизвестные реакции опор.
å МА = 0; F у × АВ + M + Q × AK - RDy × AD = 0 (1)
å М D = 0; RAy × AD - F у × В D + M - Q × KD = 0 (2)
å F i х = 0; RA х - F х = 0 (3)
6. Определяем реакции опор балок R Ay, R Dy и RA х решая уравнения.
Из уравнения ( 1 ) получаем
R Dy = F у × АВ + M + Q × AK / AD = 10 × 1 + 10 + 2 × 3 / 4 = 6,5 кН
Из уравнения ( 2 ) получаем
RAy × = F у × В D - M + Q × KD / AD =10 × 3 - 10 + 2 / 4 = 5,5 кН
Из уравнения ( 3 ) получаем
RA х = F х = F × с os 30 ° = 20 × 0,866 = 17, 32 кН
7. Проверяем правильность найденных результатов:
å Fi y = 0; RAy - F у - Q + RDy = 5,5 - 10 - 2 + 6,5 = 0
Условие равновесия å F i y = 0 выполняется, следовательно, реакции опор найдены верно.








