Примеры решения задач по теме: Задачи на составление уравнений прямой на плоскости.
1.Составить уравнение прямой, проходящей через т. М (1; 1) параллельно прямой у = 2х + 1.
Решение: Рассмотрим исходные данные задачи, используем уравнение прямой с угловым коэффициентом, проходящей через заданную точку:
у – у0 = k (х – х0).
В заданном уравнении k 1 =2, учитывая условие параллельности прямых k 1 = k 2 , имеем, что k 2 = 2. Известно, что т. М (1; 1) принадлежит прямой, подставим координаты точки М в заданное уравнение, тогда искомое уравнение примет вид:
у – 1 = 2(х – 1);
у = 2х – 1.
Ответ: у = 2х – 1.
2. Составить уравнение прямой, проходящей через т. N (3; 1) перпендикулярно прямой у = – 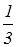 х + 2.
х + 2.
Решение: Рассмотрим общий вид уравнения прямой с угловым коэффициентом и проходящей через заданную точку:
у – у0 = k (х – х0).
В заданном уравнении k 1= – 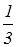 , учитывая условие перпендикулярности прямых k 1 = –1/ k 2 , получаем, что k 2 = 3.
, учитывая условие перпендикулярности прямых k 1 = –1/ k 2 , получаем, что k 2 = 3.
Так как точка N (3; 1) принадлежит прямой, подставим координаты точки в уравнение. Тогда уравнение примет вид:
у – 1 = 3 · (х – 3);
у = 3х – 8.
Ответ: у = 3х – 8.
3.Составить уравнение прямой, проходящей через т. А (5; 2) и отсекающей на осях системы координат равные отрезки.
Решение: Рассмотрим уравнение прямой в отрезках 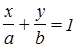 , подставим координаты точки А в уравнение с учетом того, что прямая отсекает на осях одинаковые отрезки. Предположим, что длина отрезка равна а, тогда имеем
, подставим координаты точки А в уравнение с учетом того, что прямая отсекает на осях одинаковые отрезки. Предположим, что длина отрезка равна а, тогда имеем 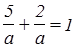 , откуда получим,
, откуда получим,
что а = 7. Тогда уравнение прямой примет вид:
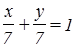 , или х + у = 7
, или х + у = 7
Ответ: х + у = 7.
4.В Δ АВС: А (-2; 0), В (2; 4), С (4; 0), АЕ – медиана. Найти длину медианы АЕ и составить ее уравнение.
Решение:
Если АЕ – медиана, то Е (х1, у1 )- середина отрезка ВС.
Найдем координаты середины отрезка:
х1 = 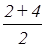 =
= 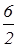 = 3
= 3
у1 = 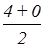 = 2 , итак, точка Е (3; 2).
= 2 , итак, точка Е (3; 2).
Длина отрезка |AE| = 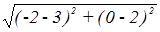 =
= 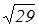
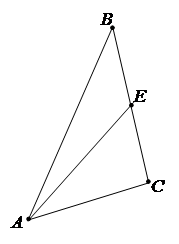 Уравнение медианы: воспользуемся уравнением прямой, проходящей через две точки А и Е:
Уравнение медианы: воспользуемся уравнением прямой, проходящей через две точки А и Е:
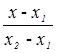 =
= 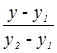 ; тогда
; тогда 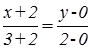 ;
;
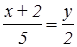 ;
;
5у – 2х – 4 = 0.
Ответ: |AE| = 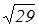 , 5у – 2х – 4 = 0.
, 5у – 2х – 4 = 0.








