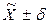4. Интервальные оценки параметров распределения

Дата: 2025-06-02; Просмотры: 13

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

При выборке небольшого объёма точечная оценка 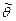может существенно отличаться от истинного значения параметра, то есть приводить к грубым ошибкам. Поэтому в случае малой выборки часто используют интервальные оценки.

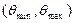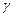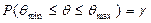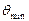Интервальной оценкой называют числовой доверительный интервал , определяемый по результатам выборки, относительно которого можно утверждать с определённой, близкой к единице вероятностью , что он заключает в себе значение оцениваемого параметра генеральной совокупности, то есть , где и 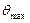называют также нижней и верхней границами доверительного интервала параметра θ.

Вероятность γ = 1 – α принято называть доверительной вероятностью (надёжностью) оценки параметра θ. Выбор значения доверительной вероятности следует производить исходя из требуемого в конкретной задаче уровня значимости α.

Чтобы получить представление о точности и надёжности оценки 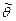параметра θ, можно для каждой близкой к единице вероятности γ указать такое значение δ, что .

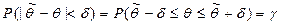Оценка будет тем точнее, чем меньше для заданной доверительной вероятности γ будет δ. Нижняя граница доверительного интервала: 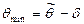, верхняя граница доверительного интервала: 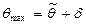, величина доверительного интервала .

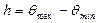Из указанного соотношения следует, что вероятность того, что доверительный интервал 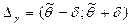со случайными границами накроет неизвестный параметр θ, равна γ. Величину δ, равную половине величины h доверительного интервала называют точностью оценки: .

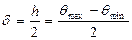В общем случае границы доверительного интервала 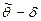и 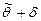есть некоторые функции от результатов наблюдений X₁, X₂, ..., X_n. Вследствие случайного характера выборки при многократном её повторении будут изменяться как положение, так и величина доверительного интервала.

Рассмотрим теперь правила построения доверительных интервалов для некоторых параметров распределений.

1). Интервальные оценки для генеральной средней (математического ожидания)

Правила построения доверительного интервала для математического ожидания зависит от того, известна или не известна дисперсия генеральной совокупности σ².

Пусть из генеральной совокупности X с нормальным законом распределения N(μ; σ) и известным генеральным средним квадратическим отклонением σ взята случайная выборка X₁, X₂, ..., X_n объёмом n и вычислено 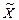. Требуется найти интервальную оценку для математического ожидания μ. Используем среднюю арифметическую 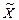, которая имеет нормальное распределение с параметрами .

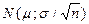Тогда статистическая оценка 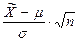имеет нормированное нормальное распределение с параметрами N(0;1). Вероятность любого отклонения 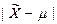может быть вычислена по интегральной теореме Лапласа для интервала, симметричного относительно μ, по формуле:

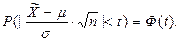
Задавая определённую доверительную вероятность γ по таблице интегральной функции вероятностей Ф(t), можно определить значение t_γ. Для оценки математического ожидания преобразуем предыдущую формулу:

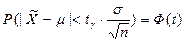
и далее будем иметь:

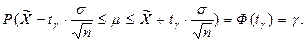
Интервал, определённый по этой формуле, и представляет собой доверительный интервал для математического ожидания μ, причём t_γ= Ф^-1(γ).

Точность оценки генеральной средней (предельная ошибка выборки) равна:

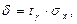
где σ_х – средняя квадратическая (стандартная) ошибка выборки, которая рассчитывается:

а) в случае повторной выборки: ;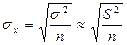

б) в случае бесповторной выборки: .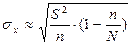

Эта формула в практических приложениях занимает особое место. По этой формуле можно, например, вычислить объём случайной выборки n, необходимый для оценки нормальной средней с заданной надёжностью γ и точностью δ, а также при заданной точности δ и известном объёме выборки n можно определить надёжность (доверительную вероятность) γ.

Нижняя и верхняя границы доверительного интервала равны:

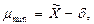
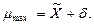
Ширина доверительного интервала равна h = μ_max – μ_min = 2δ.

Доверительная вероятность попадания генеральной средней в интервал, симметричный относительно точечной оценки математического ожидания (выборочной средней) определяется следующим образом:

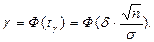
Доверительная вероятность попадания генеральной средней μ в интервал (μ₁; μ₂) вычисляется с помощью интегральной функции Лапласа:

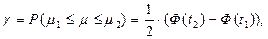
где 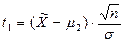и .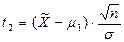

Предположим теперь, что генеральная совокупность X распределена по нормальному закону N(μ; σ) с неизвестным средним квадратическим отклонением σ.

В этом случае для построения интервальной оценки генеральной средней μ используется статистическая оценка 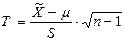, имеющая распределение Стьюдента с числом степеней свободы k = n – 1.

Предполагается, что средняя арифметическая 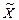и выборочное среднее квадратическое отклонение S определены по результатам выборки объёмом n из генеральной совокупности X.

По таблице t-распределения Стьюдента для k = n – 1 степеней свободы находим значение t_α,k, для которого справедливо равенство:

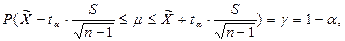
где точность оценки генеральной средней равна:

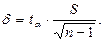
При достаточно больших n различие между доверительными интервалами при известной и неизвестной дисперсии, мало, так как при n → ∞ распределение Стьюдента стремится к нормальному распределению.

Пример 1. По результатам n = 10 наблюдений установлено, что средний темп роста акций предприятий отрасли равен 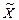= 104,4%. В предположении, что ошибки наблюдений распределены по нормальному закону со средним квадратическим отклонением σ = 1%, определить с надёжностью γ = 0,95 интервальную оценку для генеральной средней μ.

Решение. Интервальную оценку будем искать при условии известного параметр σ. По таблице интегральной функции Лапласа Ф(t) из условия γ = 0,95 найдем t_γ = 1,96.

Тогда точность оценки равна:

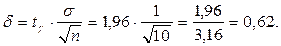
Отсюда доверительный интервал имеет вид:

104,4 – 0,62 ≤ μ ≤ 104,4 + 0,62

и окончательно 103,78 ≤ μ ≤ 105,02 (%).

Найдём доверительную вероятность, с которой можно утверждать, что средний темп роста акций окажется в пределах от 104% до 106%.

Определим значения t₁ и t₂ для нормального распределения:

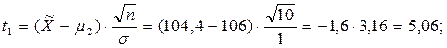
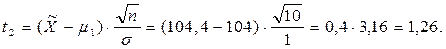
Тогда .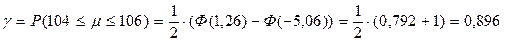

Пример 2. Средняя урожайность пшеницы на 17 опытных участках области составила 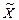= 25 ц/га, а S = 2 ц/га. Найти с надёжностью 0,9 границы доверительного интервала для оценки генеральной средней.

Решение. В данном случае генеральное среднее квадратическое отклонение σ неизвестно.

Из таблиц t-распределения для числа степеней свободы k = n – 1 = = 17 – 1 = 16 и α = 1 – γ = 1 – 0,9 = 0,1 найдём t_α =1,746.

Тогда точность оценки равна:

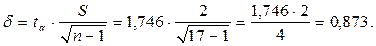
Отсюда доверительный интервал равен:

25 – 0,873 ≤ μ ≤ 25 + 0,873

и окончательно 24,127 ≤ μ ≤ 25,873 (ц/га).

Найдём доверительную вероятность, с которой урожайность пшеницы окажется в интервале от 23,94 до 26,06 ц/га. Этот интервал симметричен относительно выборочной средней 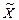= 25 ц/га с точностью оценки δ = 1,06. Тогда коэффициент доверия по распределению Стьюдента составит:

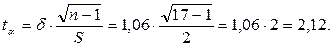
Отсюда γ = 1 – α = 1 – St(t_α; k = n – 1) = 1 – St(2,12; 16) = 1 – 0,05 = 0,95.

2). Интервальные оценки для генеральной дисперсии и среднего квадратического отклонения

Пусть из генеральной совокупности X, распределённой по нормальному закону N(μ;σ), взята случайная выборка объёмом n и вычислена выборочная дисперсия S². Требуется определить с надёжностью γ интервальные оценки для генеральной дисперсии σ² и среднего квадратического отклонения σ при малом объёме выборки (n ≤ 30).

Построение доверительного интервала для генеральной дисперсии основывается на том, что случайная величина 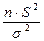имеет распределение Пирсона (χ²) с k = n – 1 степенями свободы.

Для выбранной доверительной вероятности γ = 1 – α, учитывая, что 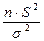имеет распределение χ² с k = n – 1 степенями свободы, можно записать:

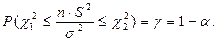
Далее по таблице χ²-распределения нужно выбрать такие два значения 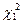и 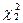, чтобы площадь, заключённая под дифференциальной функцией распределения χ² между 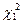и 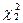, была равна γ = 1 – α.

Обычно 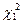и 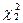выбирают так, чтобы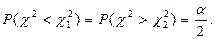

Тогда имеем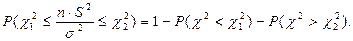

Так как таблица χ²-распределения содержит лишь 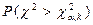, то для вычисления 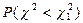запишем следующее тождество: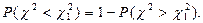

Осуществив подстановку значений, получим:

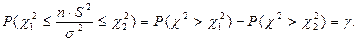
Отсюда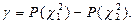

Эта формула используется при решении обратной задачи – нахождении доверительной вероятности по заданному доверительному интервалу генеральной дисперсии.

Причём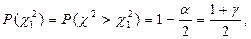

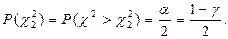
Преобразовав двойное неравенство 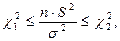окончательно получим:

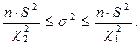
Это и есть доверительный интервал для генеральной дисперсии, когда неизвестно значение генеральной средней и по выборке объёмом n вычисляется выборочная дисперсия S².

Ширина доверительного интервала для генеральной дисперсии равна:

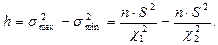
Доверительный интервал для генерального среднего квадратического отклонения σ при n ≤ 30 равен:

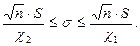
При достаточно больших объёмах выборки (n > 30) значения 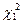и 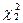определяют по формулам:

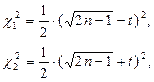
а доверительный интервал для генерального среднего квадратического отклонения определяется по формуле:

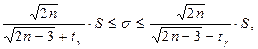
где t – нормированное значение нормальной случайной величины, соответствующее заданной надёжности γ и определяемое по таблице функции Лапласа Ф(t).

Пример 3. По результатам контроля n = 9 деталей вычислено выборочное среднее квадратическое отклонение S = 5 мм. В предположении, что ошибка изготовления деталей распределена нормально, определить с надёжностью γ = 0,95 доверительный интервал для параметра σ.

Решение. Так как n < 30, то используется χ²-распределение:

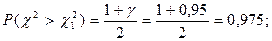
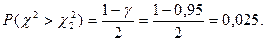
По таблице χ²-распределения для числа степеней свободы k = n – 1 = 8 и найденных вероятностей 0,975 и 0,025 определяем, что 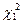= 2,180 и 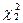= 17,535.

Вычисляем 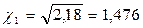и .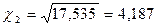

Доверительный интервал для среднего квадратического отклонения равен:

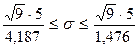
и окончательно получаем: 3,6 ≤ σ ≤ 10,2 (мм).

3). Интервальные оценки для генеральной доли

Пусть в n независимых испытаниях некоторое событие A, вероятность появления которого в каждом испытании равна p, имело место m раз, где 0 ≤ m ≤ n. В качестве основы интервальной оценки генеральной доли используется точечная оценка вероятности – частость m / n (выборочная доля), где m – число элементов выборочной совокупности, обладающих данным признаком, n – объём выборочной совокупности.

При достаточно больших n (n > 30) можно считать, что частость 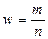имеет приближённо нормальное распределение с параметрами 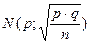. В этом случае доверительный интервал для генеральной доли p определяется соотношением:

,

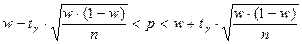где t_γ определяется по таблице интегральной функции Лапласа Ф(t):

w – частость события A;

1− w – частость противоположного события Ā;

n – объём выборки.

Точность оценки генеральной доли p равна:

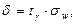
где σ_w – средняя квадратическая (стандартная) ошибка выборочной доли, которая рассчитывается по следующим формулам:

а) в случае повторной выборки: ;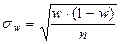

б) в случае бесповторной выборки: .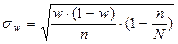

Тогда доверительный интервал для генеральной доли p будет иметь следующие границы:

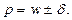
Если задан доверительный интервал для оценки генеральной доли или вероятности (p_min; p_max) при большом объёме выборки, то надёжность попадания вероятности в заданный интервал определяется из условия:

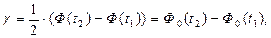
где , .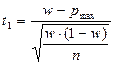

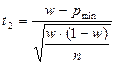Пример 4. Из партии, содержащей 2000 деталей для проверки качества было случайно отобрано 50 деталей, среди которых 4 оказались нестандартными. Определить границы доверительного интервала, в которых с надёжностью 0,954 заключена генеральная доля нестандартных изделий во всей партии.

Решение. Находим выборочную долю:

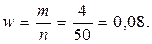
Коэффициент доверия по нормальному распределению при заданном уровне надёжности равен: t_γ = 2. Тогда точность оценки генеральной доли составит:

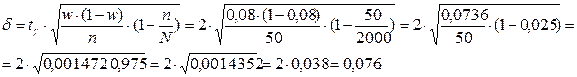
Границы доверительного интервала для генеральной доли:

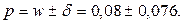
Таким образом, доля нестандартных изделий во всей партии с вероятностью 0,954 составляет: 0,004 ≤ p ≤ 0,156.

Пример 5. При испытании зерна на всхожесть из n = 400 зёрен проросло m = 384. С надёжностью γ = 0,9812 определить доверительный интервал для генеральной доли p.

Решение. По таблице интегральной функции Лапласа из условия γ = Ф(t_γ) = 0,9812 определяем t_γ = 2,35.

Учитывая, что 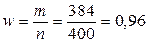, определим точность оценки:

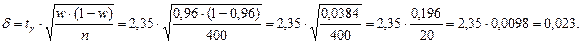
Доверительный интервал равен:

0,96 – 0,023 ≤ p ≤ 0,96 + 0,023

и окончательно 0,937 ≤ p ≤ 0,983.

Таблица 1. Основные формулы, используемые при интервальном оценивании параметров распределений

Оцениваемый параметр	Условия оценки	Используемое распределение	Точность оценки	Доверительный интервал
Генеральная средняя μ	σ известно	Ф(t)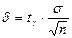
	σ не известно	S(t)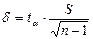
Генеральная дисперсия σ2 (или σ)	n ≤ 30	χ2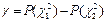
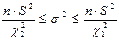
	n > 30	Ф(t)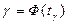
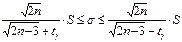
Генеральная доля p		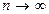Ф(t)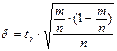

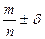
Таблица 2. Основные формулы для определения объёма выборки

Объём выборки N	Повторный отбор	Бесповторный отбор
При определении среднего размера признака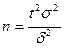
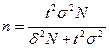
При определении доли признака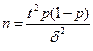

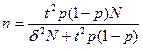
Вместо неизвестных характеристик генеральной совокупности – генеральной дисперсии σ² и генеральной доли p – обычно используют выборочную дисперсию S² и выборочную долю w.