Тема 4. Методы и модели сетевого планирования и управления.
Студентам следует изучить особенности задач, решаемых методами СНУ, которые заключаются в многосвязности и взаимообусловленности множества работ, состоящих в логической связи и очередности выполнения и в целом представляют комплекс. К таким задачам относятся: открытие нового коммерческого предприятия, проведение капитального ремонта, подготовка и проведение оптовых и розничных ярмарок, перевод магазина на самообслуживание, строительство магазина,' базы, разработка плана развития торговой сети, организация поставки товаров в городе и др.
В содержании сетевого моделирования следует обратить внимание на основные понятия, определения и графические обозначения: работ, событий фиктивных работ, путей, критических путей, сетевой модели.
Необходимо усвоить порядок подготовки задач к решению методами СНУ, который включает ряд этапов: расчленение комплекса работ на элементарные, пояснение логических связей между работами, очередности их выполнения, указание предшествующих (опорных) для каждой работы, определение ресурсов (длительность, затраты) для выполнения каждой работы, установление правил вычисления для случая возможного перераспределения ресурсов, представление всех сведений компактно, в виде специальной структурно-временной таблицы.
Особенно необходимо обратить внимание на экономико-математическую постановку задачи, выявление ее показателей в качестве которых, например, могут быть:
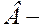общие затраты по выполнению всего комплекса работ;
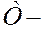время выполнения всего комплекса работ;
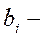выделенные ресурсы для 
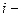й элементарной работы;
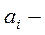обозначение 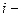й элементарной работы;
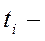длительность выполнения элементарной работы 
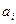выделенными ресурсами 
;
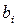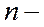число работ,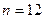 
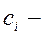коэффициент пересчета ресурсов, 
.
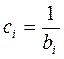Из них осуществляют выбор экономического показателя эффективности, по которому определяется успех выполнения всего комплекса pa6oт, например, время выполнения работ Т или общие затраты В. В качестве критерия эффективности, например, выбираем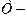 
время, которое желательно иметь минимальным из возможных значений.
Следует иметь в виду, что первый вариант распределения ресурсов В по элементарным работам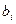 
, определяет 
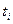длительности их выполнения, т.е. 
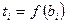. На этом основании целевую функцию в обобщенном вид можно записать так:
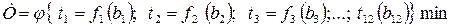
Задача состоит в поиске минимального значения времени выполнена всего комплекса работ при заданных ограниченных ресурсах В путем и: оптимального распределения между работами.
Поскольку управляемыми параметрами являются ресурсы элементарных работ 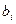, определяющие длительность их выполнения 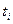то мы будем, стремиться найти новый вариант распределения ресурсов В путем переноса с одних работ части ресурсов на другие так, чтобы общий срок выполнения комплекса был минимальным.
Формально постановку задачи можно представить таким образом:
-найти новый вариант перераспределения ограниченных ресурсов B между элементарными работами:
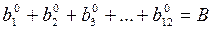
-и такие не отрицательные значения длительности их выполнения
,
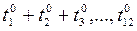которые при заданных ограничениях
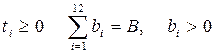
обращали бы в минимум функцию цели.
Построение сетевых моделей производят по определенным правилам строится трафарет событий; наносят на трафарет в соответствии со структурно-временной таблицей последовательно все работы м события, между одной парой событий может быть изображена только одна работа. Если две пары работ начинаются параллельно в одном событии и оканчиваются в другом узле, то вводят фиктивную работу с нулевой продолжительностью, чтобы избежать параллельных стрелок; на сетевом графике не должно быть стрелок, которые ни откуда не выходят и никуда не входят; проводится преобразование геометрии взаимного расположения работ и событий к виду, удобному для восприятия в целом, например, устраняются пересечения на графике, проводится нумерация событий слева направо и сверху вниз и др.
При решении задач № 41-50 следует придерживаться следующей последовательности.
Строят сетевой график на основе исходных данных задачи в соответствии со структурно-временной таблицей.
Определяют все возможные пути перехода из начального бытия в конечное. Анализ сетевой модели проводят с целью выявления резервов и наиболее напряженных операций.
Вычисляют длительности всех путей перехода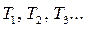 
от начального события к завершающему. Это необходимо для определения времени выполнения всего комплекса работ для первоначального варианта распределения ресурсов.
Определяют критический путь и его длительность по модели:
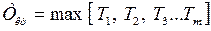
Длительность пути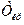 
максимальна, не включает целого ряда работ других путей, но они выполняются параллельно, поэтому за это время 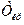все работы комплекса будут выполнены. Следовательно, минимальное время, за которое может быть выполнен весь комплекс работ, составляет 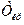. Этот путь называют критическим, он не имеет резерва, поскольку его работы наиболее напряжены и запаздывание сроков выполнения любой работы сразу приводит к увеличению продолжительности выполнения всего комплекса, а в итоге - к невыполнению плановых заданий.
Находят резервы времени по каждому пути Ti по формуле:
.
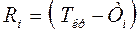Строят сетевой график в масштабе времени, начиная с критического пути 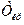, у которого 
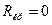, для определения работ комплекса, которые непосредственно имеют резервы. При этом сталкиваются с необходимостью введения фиктивных работ и фиктивных событий в местах расположения резервов.
Оптимизацию сетевого плана проводят последовательно по этапам путем переноса на работы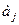 
критического пути 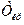с некритических работ а части средств 
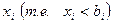, которые находят математическими методами. Задача оптимизации решается методом последовательного перехода от одного пути к другому до тех пор, пока все работы не будут лежать на критических путях и не будут иметь резервов времени. Перенося резервы с некритических работ на критические, мы будем увеличивать некритический путь и уменьшать критический до тех пор, пока не совпадут длительности всех путей. Для этого вначале располагают длительности всех путей последовательно, в порядке увеличения их резервов и начинают оптимизацию с первой пары путей 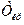и ближайшего по длительности к критическому. Это позволяет в итоге получить новый вариант распределения ресурсов 
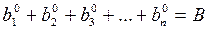и соответственно другие длительности работ 
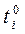, участвующих в оптимизации и приводящих к тому, что все работы комплекса будут критическими, не иметь резервов для сокращения длительности времени выполнения всего комплекса работ.
Строят оптимальный сетевой план работ с учетом новых значений длительностей работ, которые изменились в процессе оптимизации. Этот план является оптимальным, поскольку все его работы лежат на критических путях и не имеют резервов. Следует заметить, что поскольку мы переносим резервы с некритических работ на критические произвольно, полученный оптимальный план не является единственным.
Определяют экономию по критерию времени по формуле:
.
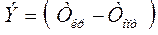Вопросы для самопроверки.
1. Назовите основные термины и определения СПУ.
2. Дайте определение критического пути.
3. Назовите критерии оптимизации сетевой модели.
4. 4 .Перечислите правила построения сетевого графика.
5. Что включает анализ сетевой модели?
6. В чем состоит содержание оптимизации сетевого графика?
7. Какой сетевой план является оптимальным?
8. Перечислите задачи коммерческой деятельности, пригодные для решения методами СПУ.