Этап 3 – анализ устойчивости САР с использованием критерия Михайлова.
Известно, что критерий Михайлова основан на анализе частотных свойств характеристического полинома D( s) замкнутой системы при подстановке s = i × w . Если годограф Михайлова D(i × w) построен на комплексной плоскости, то для устойчивости замкнутой САР необходимо и достаточно, чтобы при изменении w от нуля до бесконечности линия годографа поочередно переходила из квадранта в квадрант в положительном направлении (против часовой стрелки), причем изменение аргумента D arg D(i × w) = n × p/2 , где n – порядок системы.
Замкните обратную связь, введя в диалоговом окне блока Главное сравнивающее устройство значение 2-го весового коэффициента –1 (минус 1). Верните исходное значение коэффициента усиления в блоке c подписью W_1( s) (k1 = 1).
Выполните «контрольное» моделирование переходного процесса и убедитесь, что переходной процесс расходящийся, следовательно исходная САР неустойчива.
При открытии диалогового окна Параметры частотного анализа его вид будет таким же, как и на рисунке 3.2. Переместите курсор на кнопку Годографов и выполните щелчок левой клавиши «мыши»: появится графическое окно с заголовком Годографы и кнопка Годограф Михайлова станет активной (шрифт текста в кнопке изменит цвет с блеклого на черный). Выполните щелчок левой клавиши «мыши» по кнопке Годограф Михайлова: в Графическом окне начнется отображение результатов расчета. По завершении расчета посредством меню Графического окна и опции Свойства измените параметры осей координат на графике годографа Михайлова, так как это выполнено на рисунке 3.15. Анализ графика на рисунке 3.15 показывает, что при изменении w от 0 до ¥ изменение аргумента D arg D(i × w) = 2 × p (так как порядок САР равен 4, а цена деления по оси абсцисс на 3 порядка больше, чем по оси ординат), однако поведение линии годографа в окрестности начала координат в таком масштабе графика не определимо. Выполните «вырезание» фрагмента графика в окрестности начала координат посредством изменения в диалоговом окне Настройка параметров осей координат (см. рисунок 3.16).
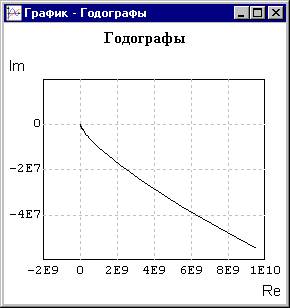
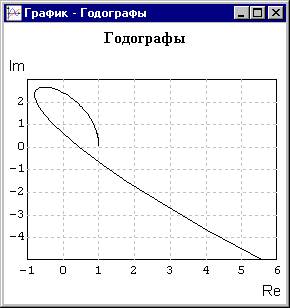
Рисунок 3.15 Рисунок 3.16
Поведение кривой Михайлова на рисунке 3.16 показывает, что последовательный переход из квадранта в квадрант не соблюдается: точка (1, 0) при w = 0 ® 1-ый квадрант ® 2-ой квадрант ® 1-ый квадрант ® 4-ый квадрант.
Резюме: исходная САР неустойчива.
Закройте диалоговое окно Параметры частотного анализа (щелчок «мышью» по кнопке Да). Измените значение k1 (k1 = 0.35). Выполните «контрольный» расчет переходного процесса и убедитесь, что его вид соответствует рисунку 2.14.
Откройте снова диалоговое окно Параметры частотного анализа. Выполните щелчок левой клавишей «мыши» по кнопке Годографов: снова откроется специальное Графическое окно с заголовком Годографы.
Выполните щелчок левой клавиши «мыши» по кнопке Годограф Михайлова: в Графическом окне начнется отображение результатов расчета. По завершении расчета посредством командного меню Графического окна и опции Свойства измените параметры осей координат на графике годографа Михайлова, так как это выполнено на рисунке 3.17. Вид кривой Михайлова на рисунке 2.31 показывает, что при изменении w от нуля до бесконечности изменение аргумента D arg D(i × w) = 2 × p, однако поведение линии годографа в окрестности начала координат в этом масштабе графика также не определимо. Выполните «вырезание» фрагмента графика в окрестности начала координат посредством изменения в диалоговом окне Настройка параметров осей координат (рисунок 3.18).
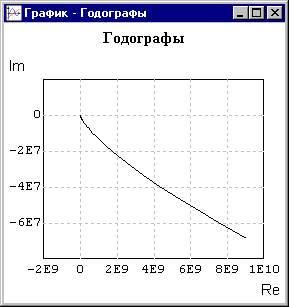
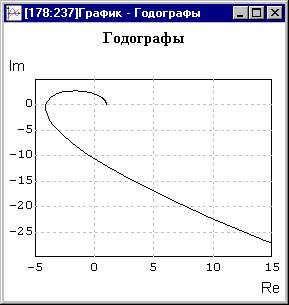
Рисунок 3.17 Рисунок 3.18
Поведение кривой Михайлова на рисунке 3.18 показывает, что последовательный переход из квадранта в квадрант соблюдается: точка (1, 0) при w = 0 ® 1-ый квадрант ® 2-ой квадрант ® 3-ий квадрант ® 4-ый квадрант.
Резюме: исходная САР устойчива.
Закройте диалоговое окно Параметры частотного анализа (щелчок «мышью» по кнопке Да): на экране монитора снова Схемное окно (см. рисунок 3.1).
3.2 Определение полюсов, нулей и коэффициентов передаточных функций
Верните исходное значение скоростной эффективности интегрирующего регулятора (k1 = 1). Разомкните Главную обратную связь (2-ой весовой коэффициент в Главном сравнивающем устройстве должен быть равен нулю). Выполните щелчок «мышью» по кнопке Старт (структурная схема разомкнутой САР инициализировалась) и затем по кнопке Стоп (моделирование прервано, так и не начавшись).
Откройте меню Анализ и выберите опцию Передаточные функции: откроется диалоговое окно Расчет передаточных функций (рисунок 3.19). Переместите курсор на нижнюю справа красную стрелку и выполните щелчок «мышью»: появится номер 1 в таблице Входы-Выходы. Переместите курсор на ячейку Входы в 1-ой строке таблицы (и единственной) и выполните щелчок «мышью», нажмите на появившуюся в этой ячейке таблицы специальную кнопку и из списка переменных выберите Вход. Повторите аналогичные действия для ячейки Выходы этой же строки таблицы и выберите переменную Выход. Заполнив таблицу, Вы подготовили данные для расчета полюсов, нулей и коэффициентов передаточной функции исходной САР в разомкнутом состоянии. Диалоговое окно будет иметь вид, аналогичный рисунку 3.20.
Рисунок 3.19 Рисунок 3.20
Параметры диалоговых строк Относительное приращение для расчета Якобиана и Абсолютное приращение для расчета Якобиана можно оставить без изменений, так как в чисто линейных САР расчет параметров передаточных функций не использует данных по приращениям Якобиана. Использование данных по приращениям Якобиана имеет место в расчете параметров линеаризуемых САР (ПК «МВТУ» автоматически выполняет линеаризацию в окрестности базовой точки). Значения «по умолчанию» данных по приращениям Якобиана выбраны из личного опыта авторов ПК «МВТУ». Начинающему Пользователю рекомендуется использовать параметры «по умолчанию».
Переместите курсор на кнопку Расчет и выполните щелчок «мышью»: практически мгновенно появится информационное окно с заголовком Результаты расчета параметров передаточных функций. В верхней части этого окна приведены результаты расчета коэффициентов Знаменателя и Числителей по возрастающим степеням s, а в нижней части – полюсы и нули передаточных функций САР (рисунок 3.21).
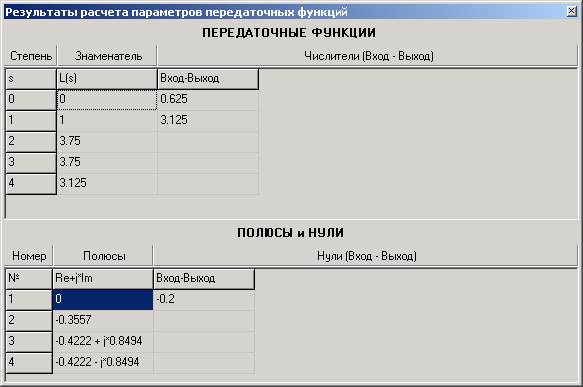
Рисунок 3.21
Учитывая, что эквивалентная передаточная функция рассматриваемой разомкнутой САР определяется не очень громоздким соотношением
,
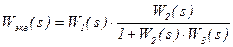прямой подстановкой исходных передаточных функций в это соотношение легко убедиться в правильности расчета программным комплексом «МВТУ» коэффициентов эквивалентной передаточной функции (выполните «ручной» расчет и сравните…).
Результаты расчета полюсов показывают, что исходная САР в разомкнутом состоянии находится на апериодической границе устойчивости, так как три полюса расположены в левой полуплоскости, а один – в начале координат.
Закройте последовательно окно Результаты расчета параметров передаточных функций (щелчок по «крестику» в правом верхнем угле окна) и затем окно Расчет передаточных функций (щелчок по кнопке Да): на экране монитора снова Схемное окно.
Замкните Главную обратную связь. В диалоговом окне блока с подписью Вход измените имя переменной на новое – Input. Выполните щелчок «мышью» по кнопке Старт (структурная схема замкнутой САР инициализировалась) и затем по кнопке Стоп (моделирование прервано, так и не начавшись).
В командном меню Анализ выберите опцию Передаточные функции: откроется незаполненное диалоговое окно Расчет передаточных функций. Переместите курсор на нижнюю справа красную стрелку и выполните щелчок «мышью»: появится номер 1 в таблице Входы-Выходы. Переместите курсор на ячейку Входы в 1-ой строке таблицы и выполните щелчок «мышью», нажмите на появившуюся в этой ячейке таблицы специальную кнопку и из списка переменных выберите Input. Повторите аналогичные действия для ячейки Выходы этой же строки таблицы и выберите переменную Выход. Заполнив таблицу, Вы подготовили данные для расчета полюсов, нулей и коэффициентов передаточной функции исходной САР в замкнутом состоянии. Диалоговое окно будет иметь вид, аналогичный рисунку 3.22.
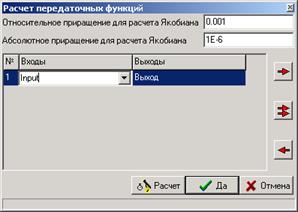
Рисунок 3.22
Выполните щелчок по кнопке Расчет в этом диалоговом окне: в открывшемся информационном окне будут приведены результаты расчета параметров передаточной функции исходной САР в замкнутом состоянии. В верхней части информационного окна приведены результаты расчета коэффициентов Знаменателя и Числителей по возрастающим степеням s, а в нижней части – полюсы и нули передаточных функций САР (рисунок 3.23).
В правильности расчета коэффициентов числителя и знаменателя передаточной функции замкнутой САР Вы можете убедиться, выполнив «ручной» расчет…
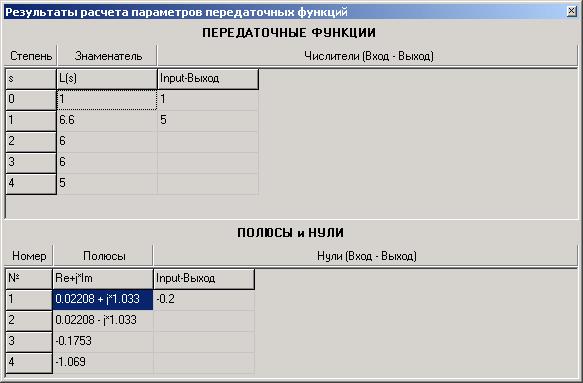
Рисунок 3.23
Анализ нижней таблицы в информационном окне еще раз подтверждает вывод об отсутствии устойчивости исходной САР в замкнутом состоянии: два действительных полюса расположены в левой полуплоскости, а два комплексно-сопряженных полюса – в правой полуплоскости.
Закройте последовательно информационное окно Результаты расчета параметров передаточных функций и затем диалоговое окно Расчет передаточных функций: на экране монитора снова Схемное окно.
Измените значение коэффициента k1 на 0.35, при котором замкнутая САР несомненно должна быть устойчивой (см. рисунок 3.11 или рисунок 3.12).
Выполните щелчок «мышью» по кнопке Старт (структурная схема замкнутой САР инициализировалась) и затем по кнопке Стоп (расчет прерван, так и не начавшись).
Откройте диалоговое окно Расчет передаточных функций (в меню Анализ опция Передаточные функции). Выполните щелчок «мышью» по кнопке Расчет: откроется окно с результатами расчета для скорректированной САР (рисунок 3.24).
Анализ нижней таблицы в информационном окне на рисунке 3.24 еще раз подтверждает вывод об устойчивости скорректированной САР в замкнутом состоянии: все четыре полюса расположены в левой полуплоскости (два отрицательных вещественных и два комплексно-сопряженных с отрицательной вещественной частью).
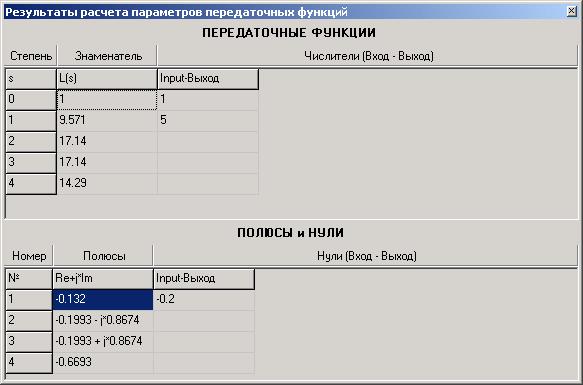
Рисунок 3.24
Закройте последовательно информационное окно и затем диалоговое окно Расчет передаточных функций: на экране монитора снова Схемное окно.
В диалоговом окне блока Вход измените имя переменной на старое – Вход.
3.3 Анализ нелинейных САР с использованием критерия В.М. Попова
3.3.1 О критерии абсолютной устойчивости В.М. Попова
Одним из точных методов (критериев) анализа устойчивости нелинейных САР, не утративших свою актуальность и в настоящее время, является критерий абсолютной устойчивости В.М. Попова.
Напомним основные положения критерия абсолютной устойчивости В.М. Попова.
В этом критерии нелинейная САР условно разделена на чисто линейную часть, обычно расположенную в прямой цепи, и чисто нелинейную часть, обычно расположенную в цепи обратной связи (рисунок 3.25).
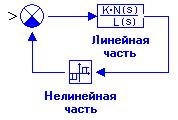
Рисунок 3.25
В «классическом» варианте доказательства данного критерия принят ряд упрощающих допущений:
1) Нелинейная часть – безинерционна.
2) Статическая характеристика нелинейной части является однозначной (без гистерезиса) и вписывается в Гурвицев угол К (0 < K < оо).
3) Линейная часть должна быть устойчивой, или в особых случаях иметь не более 2-х полюсов, расположенных на мнимой оси, при всех остальных полюсах передаточной функции, расположенных в левой полуплоскости.
4) В особых случаях должна иметь место предельная устойчивость.
В.М. Попов ввел понятие видоизмененной АФЧХ, обозначаемой обычно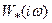 
и определяемой соотношениями:
,
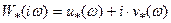где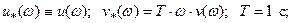 
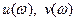- действительная и мнимая части АФЧХ линейной части, соответственно.
Существуют аналитическая и геометрическая формулировки абсолютной устойчивости по В.М. Попову.
Более наглядной является геометрическая формулировка.
Для того, чтобы имела место абсолютная устойчивость в угле [0; К] в основном и в угле [eps; К] (где ep s – бесконечно малое положительное число) в особых случаях, достаточно, чтобы в плоскости 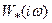можно было выбрать прямую, проходящую через точку действительной оси с абсциссой –1/ K так, чтобы годограф 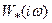весь лежал строго справа от этой прямой и чтобы, кроме того, в особых случаях имела место предельная устойчивость.
На рисунке 3.26 ниже по тексту представлена графическая иллюстрация критерия Попова при анализе устойчивости нелинейной САР, где пунктирной линией представлен традиционный годограф Найквиста (годограф АФЧХ) для линейной части САР (W_лин), сплошной линией представлен видоизмененный годограф Попова, а точка на оси абсцисс с координатой -1/K (K – Гурвицев угол) расположена левее точки пересечения годографа Попова с осью абсцисс.
Очевидно, что через точку -1/К можно провести множество прямых…
На рисунке 3.26 из множества прямых одна прямая проведена так, что видоизмененный годограф Попова лежит строго справа от этой прямой.
Резюме: нелинейная САР абсолютно устойчива.
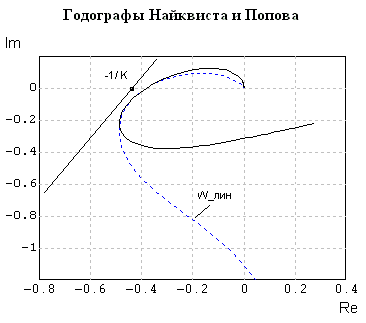
Рисунок 3.26
На этом завершим краткое изложение основных положений критерия В.М. Попова и перейдем непосредственно к выполнению очередных учебных заданий…
3.3.2 Преобразование линейной САР в нелинейную
Нелинейную САР, анализ которой будет выполнен с использованием критерия абсолютной устойчивости В.М. Попова, получим редактированием структурной схемы, созданной Вами при выполнении демонстрационно-ознакомительной задачи. Внешний вид структурной схемы должен быть примерно подобен рисунку 3.27 (сравните с рисунком 2.4)…
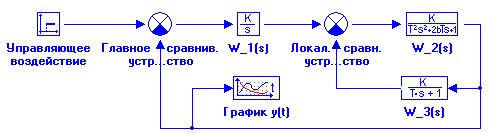
Рисунок 3.27 - Структурная схема САР
Удалите линию связи между Главным сравнивающим устройством и блоком с подписью W_1( s), а также подписи под обоими Сравнивающими устройствами (удаление подписи – процедура, обратная вводу подписи…).
Используя процедуры «перетаскивания» блоков, освободите место для вставки в структурную схему САР нового нелинейного блока (см. рисунок 3.28 ниже по тексту).
Инициализируйте библиотеку Нелинейные звенья и перенесите в Схемное окно типовой блок Релейное неоднозначное с зоной нечувствительности. Сделайте под этим блоком поясняющую подпись (Управляющее реле), соедините его линиями связи с соседними блоками.
Откройте диалоговое окно блока Управляющее реле и введите в 1-ой диалоговой строке следующие шесть параметров (через пробел): -0.02 -0.02 0.02 0.02 -1 1. Фактически нелинейный блок, добавленный в структурную, реализует однозначную нелинейность типа Релейная с зоной нечувствительности. Закройте диалоговое окно щелчком по кнопке Да.
Откройте диалоговое окно блока Интегратор (блок с подписью W_1( s)) и установите «оптимальное» значение коэффициента k1 = 0.35.
Инициализируйте библиотеку Субструктуры и перенесите в Схемное окно еще один типовой блок В память. Измените имя переменной на новое: Вход_2. Подсоедините этот блок к линии связи (рисунок 3.28).
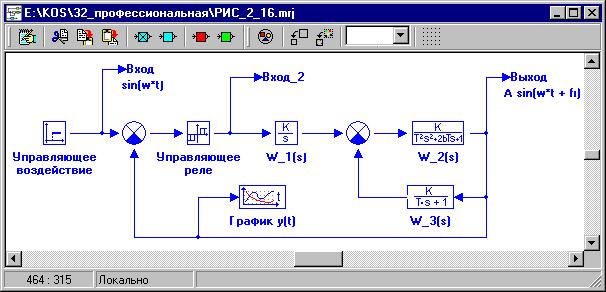
Рисунок 3.28
3.3.3 Формулировка заданий к анализу устойчивости нелинейной САР
1) Используя критерий абсолютной устойчивости В.М. Попова, определить скоростную эффективность интегрирующего регулятора (блок с подписью W_1( s)), при которой созданная нелинейная САР (см. рисунок 3.28) будет абсолютно устойчивой.
2) Определить тип устойчивости нелинейной САР, используя прямое моделирование переходного процесса в автономной системе при ненулевых начальных условиях.
3) Выполнить расчет переходного процесса в САР (нулевые начальные условия) при подаче управляющего воздействия, равного 0.8*1( t).
3.3.4 А можно ли использовать критерий В.М. Попова?
Проверим, удовлетворяет ли нелинейная часть нелинейной САР (созданной Вами) приведенным выше допущениям (см. пункты 1…4 в подразделе 3.3.1).
Для нелинейной части системы:
Типовое нелинейное звено, внесенное Вами в структурную схему, «исполняет роль» нелинейной части САР и является безинерционным (см. справку по данному блоку).
Статическая характеристика нелинейной части (нелинейного звена с введенными Вами его параметрами) не имеет гистерезиса, т.е. является однозначной и ее статическая характеристика вписывается в Гурвицев угол [0; 50] (т.к. 1/ 0.02 = 50 = К).
Для линейной части системы:
Линейная часть САР, расположенная между точками подключения переменных Вход_2 и Выход, соответствует варианту особого случая, так как она имеет один нулевой полюс (за счет блока Интегратор) при всех остальных полюсах, расположенных в левой полуплоскости (см. подраздел 3.2).
Для линейной части с введенным Вами значением скоростной эффективности привода (k1 = 0.35) существует предельная устойчивость, т.е. при замыкании линейной части отрицательной жесткой обратной связью с бесконечно малым коэффициентом усиления САР несомненно будет устойчивой.
Последнее уверенное утверждение основано на результатах, представленных в подразделе 3.1, в котором показано, что при замыкании скорректированной линейной части даже единичной обратной связью замкнутая САР является устойчивой. Поэтому при меньшем коэффициенте усиления в цепи Главной обратной связи скорректированная линейная САР в замкнутом состоянии тем более будет устойчивой.
3.3.5 Процедуры, реализующие критерий В.М. Попова
Приведите созданную Вами нелинейную САР к автономной. Для этого установите нулевую высоту «ступеньки» в диалоговом окне блока Управляющее воздействие.
Разомкните цепь Главной обратной связи, установив в диалоговом окне Главного сравнивающего устройства нулевое значение 2-го весового коэффициента.
Выполните щелчок «мышью» по кнопке Старт (структурная схема разомкнутой нелинейной САР инициализировалась) и затем по кнопке Стоп (расчет прерван).
Посредством опции Частотный анализ в командном меню Анализ откройте диалоговое окно Параметры частотного анализа и заполните его. Для этого переместите курсор на кнопку Годографов и выполните щелчок левой клавишей «мыши»: откроется графическое окно с заголовком Годографы и изменится форма диалогового окна. Переместите курсор на крайнюю левую кнопку с символом «+» и выполните два щелчка левой клавишей «мыши»: в таблице появятся две новые строки с номерами 1 и 2.
Переместите курсор на ячейку Входы 1-ой строки, выполните щелчок левой клавишей «мыши», нажмите на появившуюся в этой ячейке таблицы специальную кнопку и из списка переменных выберите Вход_2.
Повторите аналогичные действия для ячейки Входы во 2-й строке таблицы.
По аналогии с предыдущим заполните 2-й и 3-й столбцы таблицы (рисунок 3.29).
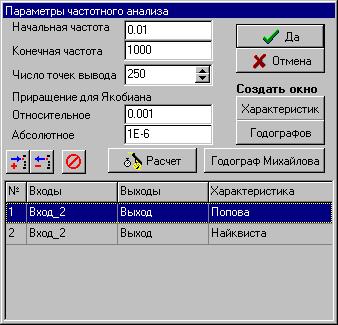
Рисунок 3.29
Переместите курсор на кнопку Расчет и выполните щелчок левой клавишей «мыши»: в поле Графического окна начнется отображение результатов расчета и заголовок окна изменится на новый – Годограф Попова, Годограф Найквиста.
Вид линий годографов в поле Графического окна будет подобным графикам на рисунке 3.30 ниже по тексту.
Используя опцию Свойства меню Графического окна измените в диалоговом окне Настройка параметры осей координат, имя и тип линии годографа Найквиста (синяя сплошная на рисунке 3.30) на пунктирный.
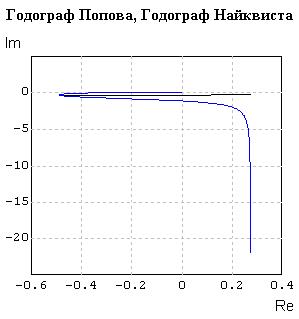
Рисунок 3.30
Для изменения имени и типа линии годографа Найквиста переместите курсор в диалоговом окне Настройка (см. рисунок 3.31 ниже по тексту) на специальную кнопку (в поле которой текст График 1), выполните щелчок «мышью» и из списка выберите График 2. Удалите текст График 2 и введите новый текст Годограф Найквиста. Переместите курсор на специальную кнопку, расположенную чуть ниже, выполните щелчок «мышью» и далее выберите новый тип линии – пунктирный.
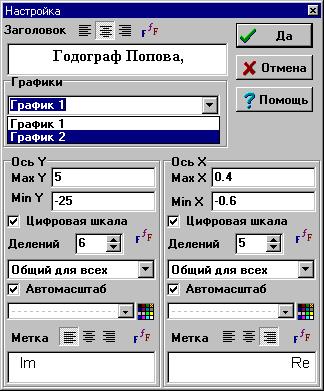
Рисунок 3.31
Аналогичным образом можно присвоить уникальное имя и линии с именем График 1 на новое – Годограф Попова. Измените параметры осей координат, как это выполнено в диалоговом окне Настройка на рисунке 3.32.
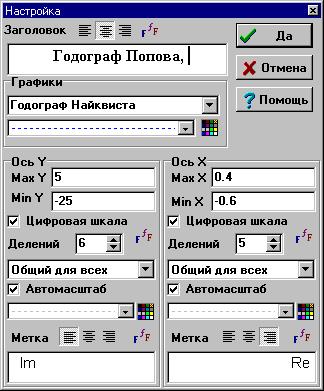
Рисунок 3.32
Переместите в диалоговом окне Настройка курсор на кнопку Да и выполните щелчок левой клавишей «мыши»: преобразованное графическое окно с линиями годографа Попова (черная сплошная) и годографа Найквиста (синяя пунктирная) будут иметь вид, аналогичный рисунку 3.33.
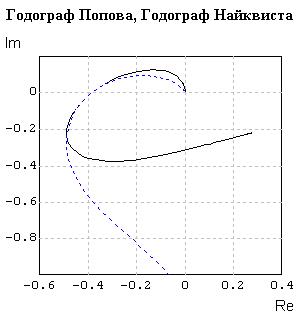
Рисунок 3.33
Одновременное отображение графиков годографа Найквиста и видоизмененного годографа Попова (см. рисунки 3.30 и 3.33) показывает, что при одном и том же значении частоты вещественные части у обоих годографов одинаковые. Поэтому точки пересечения линий этих годографов с осью абсцисс совпадают. Это позволяет во многих случаях использовать для анализа устойчивости нелинейных САР не видоизмененный годограф, а годограф Найквиста…
При частоте стремящейся к нулю годограф Попова стремится в точку с координатами (b1 – a1 × b0 , - b0), где коэффициенты a1 , b0 и b1 - коэффициенты передаточной функции линейной части САР, определяемой выражением
.
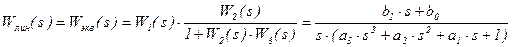Выясним, можно ли провести через точку с координатами (-1/K, 0), где К = 50 – верхняя граница Гурвицева угла, прямую так, чтобы годограф Попова лежал строго справа от этой прямой.
Из рисунка 3.33 видно, что точка с абсциссой –0.02 лежит внутри годографа Попова и любая прямая, проведенная через эту точку, пересечет линию годографа.
Этот результат свидетельствует о том, что рассматриваемая замкнутая автономная нелинейная САР (схема которой получена вставкой дополнительного нелинейного звена в структурную схему устойчивой линейной САР) не будет абсолютно устойчивой…
Проверим это утверждение прямым моделированием…
Закройте окно Параметры частотного анализа. Замкните Главную обратную связь и измените начальные условия в блоке с подписью W_2( s) на новые: 0.1 0 (через пробел).
Выполните щелчок по командной кнопке Продолжить: в поле Графического окна (блок с подписью График y( t)) будут отображены результаты расчета. Внешний вид переходного процесса будет аналогичен кривой на рисунке 3.34.
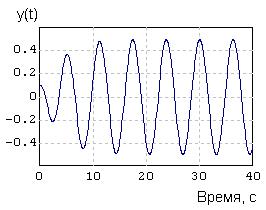
Рисунок 3.34
Вид переходного процесса показывает, что в автономной замкнутой нелинейной САР при ненулевых начальных условиях устанавливается режим приблизительно гармонических автоколебаний, амплитуда которых примерно в 25 раз превышает зону нечувствительности в блоке Управляющее реле (± 0.02).
Резюме: в данной нелинейной САР устанавливается режим относительно больших автоколебаний, поэтому САР не выполняет своих «обязанностей» (не удерживает стационарное состояние с погрешностью плюс/минус 2 %) и, следовательно такая система должна считаться практически неустойчивой. ==> Необходима новая коррекция САР…
3.3.6 Новая коррекция САР и определение типа устойчивости
Выполним новую коррекцию параметров рассматриваемой нелинейной САР.
Из графика годографа Попова следует (см. рисунок 3.33 в подразделе 3.3.5): чтобы замкнутая нелинейная САР стала устойчивой, необходимо либо уменьшить примерно в 20 раз коэффициент скоростной эффективности (k1) в интегрирующем регуляторе, либо в такое же количество раз уменьшить высоту «ступеньки» в Управляющем реле.
Реализуем первый вариант.
Откройте диалоговое окно блока Интегратор и введите в 1-ой диалоговой строке 0.35/20 (0.35 делить на 20).
Такой тип ввода параметра звена основан на том, что диалоговые строки всех типовых блоков «распознают» около 30 простейших математических операций (и операцию Деление в том числе…).
Закройте диалоговое окно и щелкните «мышью» по кнопке Продолжить…
По завершении расчета 2-х кратным щелчком левой клавиши «мыши» в поле графика выполните автомасштабирование: вид графика (рисунок 3.35) показывает, что с новым значением k1 автономная нелинейная САР асимптотически устойчива.
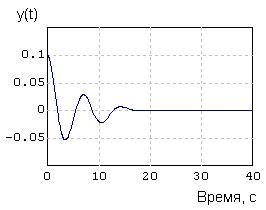
Рис. 3.35
Начальное отклонение (0.1) относительно быстро устраняется и САР асимптотически возвращается в свое равновесное состояние (y_стационарное = 0).
Резюме: скорректированная автономная нелинейная САР асимптотически устойчива.
3.3.7 Анализ устойчивости скорректированной нелинейной САР
Проверим вышеприведенный вывод об асимптотической устойчивости нелинейной САР, полученный на основании прямого моделирования переходного процесса в автономной системе при ненулевых начальных условиях…
Возвратите нулевые начальные условия в блоке W_2(s). Разомкните Главную обратную связь.
Выполните щелчок «мышью» по кнопке Старт (структурная схема разомкнутой нелинейной САР инициализировалась) и затем по кнопке Стоп (расчет прерван).
Используя опцию Частотный анализ из меню Анализ, откройте диалоговое окно Параметры частотного анализа и затем выполните в нем щелчок «мышью» по кнопке Расчет: произойдет расчет годографов при скорректированном значении k1 = 0.35/20.
Используя опцию Свойства графического окна (щелчок правой клавишей «мыши»), измените параметры осей координат так, как это выполнено на рисунке 3.36.
Точка пересечения годографа Попова с осью абсцисс расположена правее точки с абсциссой -1/К = - 0.02 (рисунок 3.36).
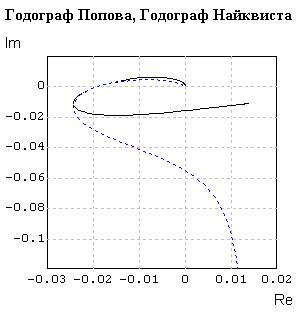
Рисунок 3.36
Уточним, на сколько правее расположена точка пересечения годографа Попова с осью абсцисс.
Переместите курсор «мыши» в поле графика, выполните щелчок правой клавишей «мыши» и в появившемся меню выберите опцию Список: графическое окно сменится на таблицу результатов расчета.
Используя вертикальную «прокрутку», найдите строку, наиболее близко соответствующую координатам пересечения годографа Попова с осью абсцисс, т.е. необходимо найти в таблице место, где мнимая часть (График 1) меняет знак с минуса на плюс. После выполнения Вами поиска окно с таблицей будет иметь вид, подобный рисунку 3.37.
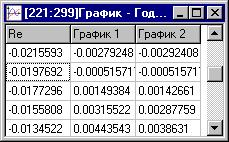
Рисунок 3.37
Из таблицы следует, что при смене знака мнимой части вещественная часть (Re) равна приблизительно - 0.0198, т.е. больше, чем – 0.02.
Поэтому через точку пересечения несомненно можно провести прямую, относительно которой годограф Попова будет расположен строго справа.
Резюме: скорректированная нелинейная замкнутая САР абсолютно устойчива.
Переместите курсор в поле таблицы, выполните щелчок правой клавишей «мыши», в появившемся меню выберите опцию Список: таблица сменится на график годографов.
Закройте диалоговое окно Параметры частотного анализа (щелчок по кнопке Да): на экране монитора снова Схемное окно.
3.3.8 Расчет переходных процессов при подаче управляющего воздействия
Выполним завершающий этап заданий, а именно: расчет переходных процессов в скорректированной нелинейной САР при подаче управляющего воздействия u( t) = 0.8*1( t).
Замкните Главную обратную связь (в диалоговом окне Главного сравнивающего устройства 2-ой весовой коэффициент должен быть равен -1).
Измените конечное время расчета на 200 с (щелчок «мышью» по командной кнопке Параметры расчета).
Выполните расчет переходного процесса (щелчок «мышью» по командной кнопке Продолжить).
График переходного процесса (рисунок 3.38) свидетельствует, что скорректированная нелинейная САР отработала управляющее воздействие, однако время переходного процесса значительно больше (около 80 с), чем в демонстрационно-ознакомительной задаче при k1 = 0.35 (там было менее 20 с).
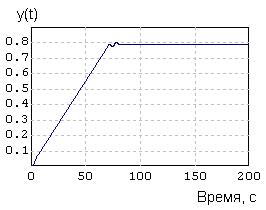
Рисунок 3.38
Выполните увеличение коэффициента скоростной эффективности регулятора k1 в 2 раза (в 1-ой диалоговой строке блока Интегратор введите 0.35/10).
Выполните щелчок «мышью» по командной кнопке Продолжить…
График переходного процесса в этом случае, представленный рисунке 3.39, свидетельствует, что в нелинейной САР установились высокочастотные (приблизительно гармонические) автоколебания с амплитудой примерно 0.05, что в 2.5 раза превышает ширину зону нечувствительности в Управляющем реле.
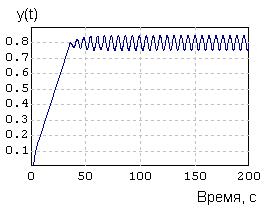
Рисунок 3.39
Резюме: нелинейная САР «плохо» отработала управляющее воздействие потому, что при таком значении k1 (0.35/10) не выполняются условия критерия абсолютной устойчивости В.М. Попова: точка на оси абсцисс, с координатой –1/ K, расположена внутри годографа Попова.
Сохраните данную задачу (нелинейную САР) под новым оригинальным именем, например, Нел_САР. mrj (посредством опции Сохранить как… из меню Файл).
На этом краткое знакомство с критерием абсолютной устойчивости В.М. Попова и его программной реализацией в ПК «МВТУ» применительно к анализу устойчивости нелинейных САР, завершено.