Тема урока: Повторение. Правила нахождения первообразных
11 класс. Алгебра. 08.02.2022г.
Тема урока: Повторение. Правила нахождения первообразных
1.Повторение изученного материала
Вопросы: (устно)
-Какая функция называется первообразной?
(Функция F(x) называется первообразной функции f(x) на некотором промежутке, если для всех x из этого промежутка 
.)
-Как называется процесс нахождения производной функции?
(Дифференцированием.)
- Каким образом показать, что функция F(x) является первообразной для функции f(x)?
(Найти производную функции F(x).)
-Скажите, является ли функция F(x)=3x2+11x первообразной для функции f(x)=6х+10?
( Нет, т.к. производная функции F(x)=3x2+11x равна 6х+11, а не 6х+10.)
-Какое количество первообразных можно найти для некоторой функции f(x)?
(Бесконечно много, т.к. к полученной функции мы всегда прибавляем константу, которая может быть любым вещественным числом.)
2.Теоретический материал
Обратную операцию нахождения первообразной для данной функции называют интегрированием (от латинского слова integrare – восстанавливать). Таблицу первообразных для некоторых функций можно составить, используя таблицу производных. Например, зная, что 
, получаем , откуда следует, что все первообразные функции 
записываются в виде 
, где C – произвольная постоянная.
Например:
,
получаем ,
откуда следует, что все первообразные функции записываются в виде , где C – произвольная постоянная.
Откройте учебники на странице 294. Здесь приведена таблица первообразных.
Правила интегрирования можно получить с помощью правил дифференцирования. Рассмотрим следующие правила интегрирования: пусть F(x) и G(x) – первообразные соответственно функций f(x) и g(x) на некотором промежутке. Тогда:
1) Функция 
является первообразной функции 
;
2) Функция 
является первообразной функции .
3) 3) функция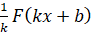 
, где 
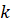и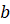 
– постоянные, причём 
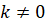, является первообразной функции 
.
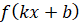3.Решение задач по теме:
А сейчас, используя правила интегрирования и таблицу первообразных, выполним несколько заданий.
Задание 1. Найдите одну из первообразных функции:
а)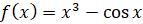 
; б)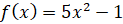 
.
Решение.
Задание 2. Найдите все первообразные функции:
а)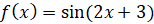 
; б)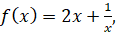 
.
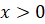Решение.
Задание 3. Для функции y = f(x) найдите множество всех первообразных. Выполните проверку. f(x) = 2sin x + 3x3
Решение:
f(x) = 2sin x + 3x3
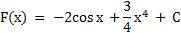
Проверка:
Найдем производную функции F(x).
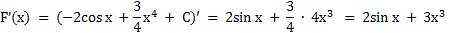
F’(x) = f(x)
Ответ: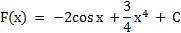 
Рассмотрим задачи 1,2 с.295 учебника
Задача 1.Найти одну из первообразных функции 
Решение:
Чтобы найти первообразную данной функции нужно использовать правило интегрирования: функция является первообразной функции . Также будем использовать таблицу первообразных для функций 
, при p=2 и для 
Находим одну из первообразных данной функции: 
Задача 2. Найти все первообразные функции 
Решение.
По таблице первообразных находим, что одной из первообразных функции 
является функция 
.Также по таблице первообразных находим, что одной из первообразных функции 
является функция 
. По правилам интегрирования одна из первообразных данной функции 
.
Это мы нашли одну из первообразных функции, а по условию задачи нужно найти все первообразные.
Значит н еобходимо к найденной первообразной прибавить константу, т.е. 
- все первообразные функции
ВИДЕО УРОК : Обязательно к просмотру
https://yandex.ua/video/preview/?text=видео%20урок%20решение%20задач%20по%20теме%20правила%20нахождения%20первообразных&path=wizard&parent-reqid=1644160768172831-17811389390351283112-man1-4246-man-l7-balancer-8080-BAL-5604&wiz_type=vital&filmId=9852403000377773968
ВИДЕО УРОК: Обязательно к просмотру
https://www.youtube.com/watch?v=hBo3KcfLScw
4.Домашнее задание: Повторить таблицу первообразных п.55.
Решить № 989(1,3,5), № 990 (1,3), №991(1-3)