Решение типовых задач
|
| Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Башкирский государственный аграрный университет» | |
Кафедра математики
Математика
Методические указания
и задания к выполнению контрольной работы
Направление подготовки бакалавриата
35.03.04 Агрономия
Профиль:
Агрономия
Уфа 2016
00УДК 51(07)
ББК 22.1я73,22.161.6
М 54
Рекомендовано к изданию методической комиссией механического факультета (протокол № 7 от 24 февраля 2016 года ) и заседанием кафедры математики (протокол № 5 от 4 февраля 2016 года)
Составители: к.ф.-м.н., доцент Маннанов М.М.,
к.ф.-м.н., ассистент Павленко В.А.
Рецензент: доцент кафедры физики Юмагужин Р.Ю.
Ответственный за выпуск: зав. кафедрой математики доцент Лукманов Р.Л.
Порядок выполнения контрольных работ
К выполнению контрольной работы следует приступать после изучения соответствующего теоретического материала по учебнику и лекциям, а также решения задач на практических занятиях.
При выполнении контрольной работы студент должен, руководствоваться следующими указаниями:
контрольную работу следует выполнять в отдельной тетради, на передней обложке которой должны быть указаны фамилия и инициалы студента, шифр, номер контрольной работы и дата её отсылки в университет;
решения всех задач и пояснения к ним должны быть достаточно подробными, рекомендуется делать соответствующие ссылки на вопросы теории с указанием формул, теорем, выводов, которые используются при решении;
все вычисления должны быть приведены полностью, чертежи и графики должны быть выполнены аккуратно, четко, с указанием единиц масштаба, координатных осей, обозначения в задачах должны соответствовать указаниям на чертеже;
для удобства рецензирования преподавателем контрольной работы следует оставлять на каждой странице поля;
после получения отрецензированной работы студент должен исправить в ней все ошибки. В случае незачета студент обязан в кратчайший срок выполнить все требования рецензента и представить работу на повторное рецензирование. Неверно выполненные задачи или вся работа заново решаются в той же тетради, исправление небольших недочетов и ошибок приводится в конце работы. До экзамена необходимо исправить все ошибки и получить зачет. Работы, выполненные небрежно, несамостоятельно, или содержащие задачи не своего варианта, возвращаются без проверки.
В период сессии на зачете или экзамене студент обязан представить зачтенную контрольную работу и по требованию преподавателя дать устные пояснения ко всем задачам, содержащимся в работе.
Контрольная работа состоит из шести заданий. В каждом задании 20 вариантов. Номер варианта студент выбирает по формуле: 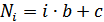 , где
, где 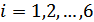 – номер задания, b и c – предпоследняя и последняя цифры шифра зачётной книжки или студенческого билета. (Номера студенческого билета и зачётной книжки совпадают).
– номер задания, b и c – предпоследняя и последняя цифры шифра зачётной книжки или студенческого билета. (Номера студенческого билета и зачётной книжки совпадают).
Например, номер студенческого билета (зачётной книжки) студента 1265. В этом случае имеем b = 6, c = 5. В первом задании этот студент выполняет вариант 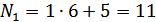 . Во втором задании:
. Во втором задании: 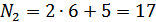 . В третьем задании
. В третьем задании 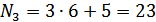 . Так как 23-го варианта нет, то студент выполняет 3-ий вариант (23-20=3) и т.д. То есть, если номер варианта превышает число 20, то нужно вычитать 20. Если превышает число 40, то вычитать уже нужно 40, если превышает 60, то вычитать уже нужно 60 и т.д. Например, для этого же студента в шестом задании вариант будет вычисляться следующим образом
. Так как 23-го варианта нет, то студент выполняет 3-ий вариант (23-20=3) и т.д. То есть, если номер варианта превышает число 20, то нужно вычитать 20. Если превышает число 40, то вычитать уже нужно 40, если превышает 60, то вычитать уже нужно 60 и т.д. Например, для этого же студента в шестом задании вариант будет вычисляться следующим образом 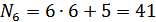 . Следовательно, студент решает первый вариант шестого задания (41-40=1).
. Следовательно, студент решает первый вариант шестого задания (41-40=1).
Бывает ещё особый случай: когда предпоследняя и последняя цифра зачётной книжки (студенческого билета) – нули. Например, номер студенческого билета (зачётной книжки) студента 1500. В таком случае студент решает в каждом задании 20-ый вариант.
Прежде чем приступать к выполнению работы, целесообразно изучить соответствующие разделы в учебниках, рекомендованных в библиографическом списке.
1. Найти указанные пределы:
1. 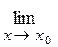
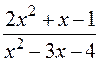

 : а)
: а) 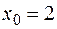 , б)
, б) 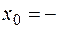 1, в)
1, в) 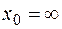 .
.
2. 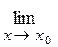
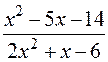

 : а)
: а) 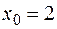 , б)
, б) 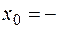 2, в)
2, в) 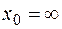 .
.
3. 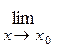
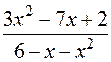
 : а)
: а) 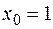 , б)
, б) 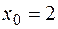 , в)
, в) 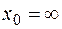 .
.
4. 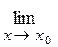
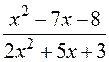 : а)
: а) 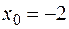 , б)
, б) 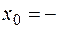 1, в)
1, в) 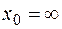 .
.
5. 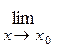
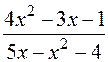 : а)
: а) 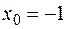 , б)
, б) 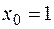 , в)
, в) 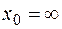 .
.
6. 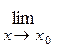
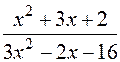 : а)
: а) 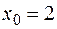 , б)
, б) 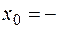 2, в)
2, в) 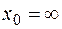 .
.
7. 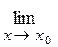
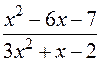 : а)
: а) 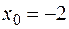 , б)
, б) 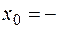 1, в)
1, в) 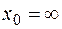 .
.
8. 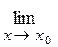
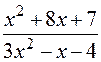 : а)
: а) 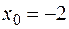 , б)
, б) 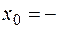 1, в)
1, в) 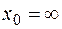 .
.
9. 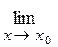
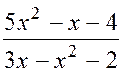 : а)
: а) 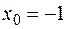 , б)
, б) 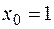 , в)
, в) 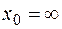 .
.
10. 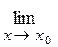
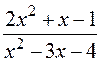 : а)
: а) 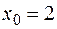 , б)
, б) 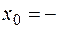 1, в)
1, в) 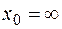 .
.
11. 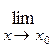
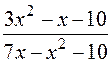 : а)
: а) 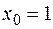 , б)
, б) 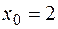 , в)
, в) 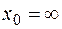 .
.
12. 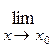
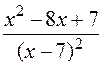 : а)
: а) 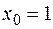 , б)
, б) 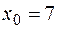 , в)
, в) 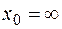 .
.
13. 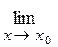
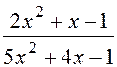 : а)
: а) 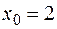 , б)
, б) 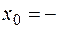 1, в)
1, в) 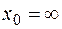 .
.
14. 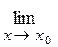
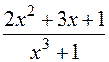 : а)
: а) 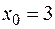 , б)
, б) 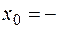 1, в)
1, в) 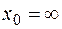 .
.
15. 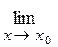
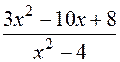 : а)
: а) 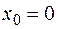 , б)
, б) 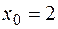 , в)
, в) 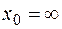 .
.
16. 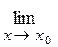
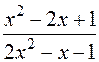 : а)
: а) 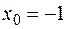 , б)
, б) 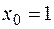 , в)
, в) 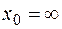 .
.
17. 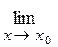
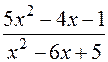 : а)
: а) 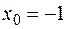 , б)
, б) 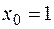 , в)
, в) 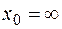 .
.
18. 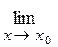
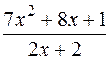 : а)
: а) 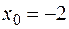 , б)
, б) 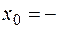 1, в)
1, в) 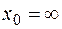 .
.
19. 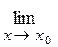
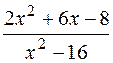 : а)
: а) 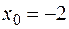 , б)
, б) 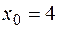 , в)
, в) 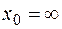 .
.
20. 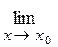
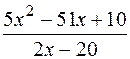 : а)
: а) 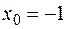 , б)
, б) 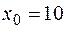 , в)
, в) 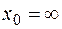 .
.
Решение типовых задач
1) 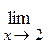
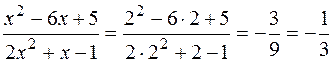 ;
;
2) 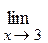

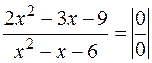 .
.
При подстановке вместо переменной x её предельного значения 3, получается неопределенность вида 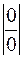 . Для избавления от этого вида неопределенности представим квадратные трехчлены числителя и знаменателя в виде произведения линейных множителей, воспользовавшись известной формулой:
. Для избавления от этого вида неопределенности представим квадратные трехчлены числителя и знаменателя в виде произведения линейных множителей, воспользовавшись известной формулой:
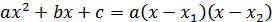 ,
,
где 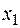 и
и 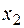 -корни квадратного трехчлена
-корни квадратного трехчлена 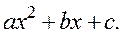
У нас 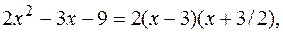 т.к. дискриминант квадратного трехчлена
т.к. дискриминант квадратного трехчлена 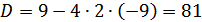 , а следовательно,
, а следовательно, 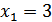 ,
, 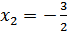 .
.
По аналогии 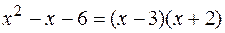 .
.
Теперь условие задачи можно переписать в другом виде и продолжить решение
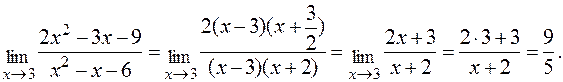
3) 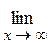
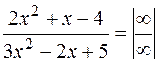 .
.
Мы получили неопределенность вида 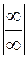 , избавиться от которой можно делением числителя и знаменателя дроби на старшую степень переменной, т.е. на
, избавиться от которой можно делением числителя и знаменателя дроби на старшую степень переменной, т.е. на 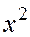 .
.
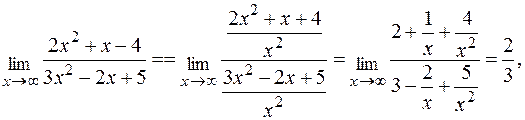
так как 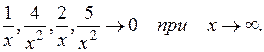 .
.
2. Найти производные заданных функций
1. а) 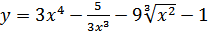 ; б)
; б) 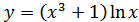 ;
;
в) 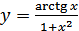 ; г)
; г) 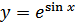 .
.
2. а) 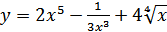 ; б)
; б) 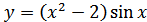 ;
;
в) 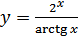 ; г)
; г) 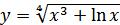 .
.
3. а) 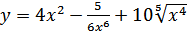 ; б)
; б) 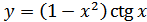 ;
;
в) 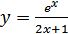 ; г)
; г) 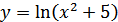 .
.
4. а) 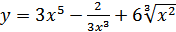 ; б)
; б) 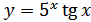 ;
;
в) 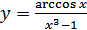 ; г)
; г) 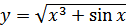 .
.
5. а) 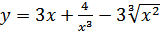 ; б)
; б) 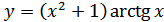 ;
;
в) 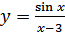 ; г)
; г) 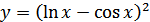 .
.
6. а) 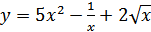 ; б)
; б) 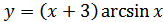 ;
;
в) 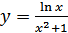 ; г)
; г) 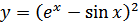 .
.
7. а) 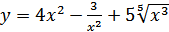 ; б)
; б) 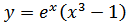 ;
;
в) 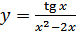 ; г)
; г) 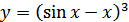 .
.
8. а) 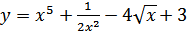 ; б)
; б) 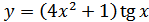 ;
;
в) 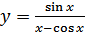 ; г)
; г) 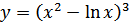 .
.
9. а) 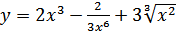 ; б)
; б) 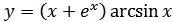 ;
;
в) 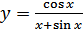 ; г)
; г) 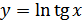 .
.
10. а) 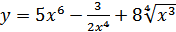 ; б)
; б) 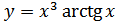 ;
;
в) 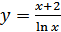 ; г)
; г) 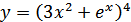 .
.
11. а) 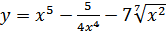 ; б)
; б) 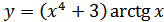 ;
;
в) 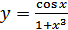 ; г)
; г) 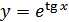 .
.
12. а) 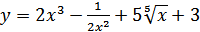 ; б)
; б) 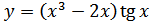 ;
;
в) 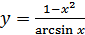 ; г)
; г) 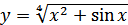 .
.
13. а) 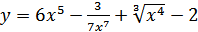 ; б)
; б) 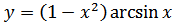 ;
;
в) 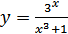 ; г)
; г) 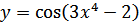 .
.
14. а) 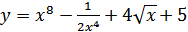 ; б)
; б) 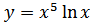 ;
;
в) 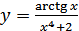 ; г)
; г) 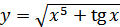 .
.
15. а) 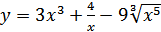 ; б)
; б) 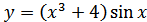 ;
;
в) 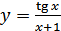 ; г)
; г) 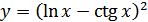 .
.
16. а) 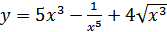 ; б)
; б) 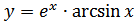 ;
;
в) 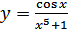 ; г)
; г) 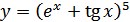 .
.
17. а) 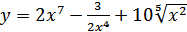 ; б)
; б) 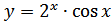 ;
;
в) 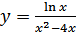 ; г)
; г) 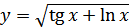 .
.
18. а) 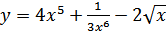 ; б)
; б) 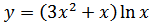 ;
;
в) 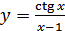 ; г)
; г) 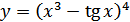 .
.
19. а) 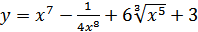 ; б)
; б) 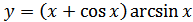 ;
;
в) 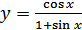 ; г)
; г) 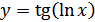 .
.
20. а) 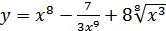 ; б)
; б) 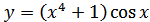 ;
;
в) 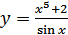 ; г)
; г) 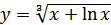 .
.
При решении всех последующих задач кроме таблиц производных будут использованы известные правила дифференцирования суммы, разности, произведения, дроби и теорема о производной сложной функции.
1. 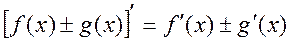 ,
,
2. 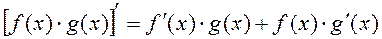 ,
,
3. 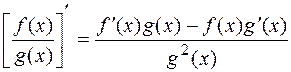 .
.
4. Если задана сложная функция y = f ( u ), где u = z ( x ),т.е. y = f ( z ( x )) и каждая из функций y и u дифференцируема по своему аргументу, то 
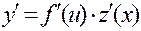 .
.
Также следует помнить, что если в знаменателе дроби стоит степень какого-либо числа, то эту дробь можно представить как отрицательную степень числа, например, 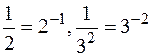 , так же
, так же 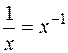 ,
, 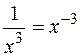 и т.д. Подкоренное выражение можно записать в виде степени, показателем которой является дробь:
и т.д. Подкоренное выражение можно записать в виде степени, показателем которой является дробь: 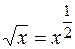 ,
, 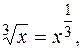
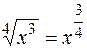 ,
, 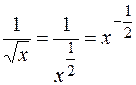 ,
, 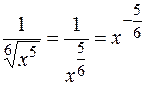 ,
, 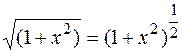 ,
, 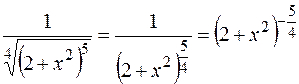 и т.д.
и т.д.
Решение типовых задач
Найти производные заданных функций
а) 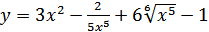 ; б)
; б) 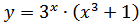
в) 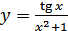 ; г)
; г) 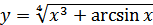 .
.
Решение.
а) В этом случае пользуемся правилом: производная суммы равна сумме производных. Также пользуемся табличной производной: 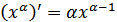 . Представим каждое слагаемое в виде степени. Получаем:
. Представим каждое слагаемое в виде степени. Получаем:
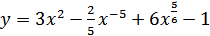 . Отсюда следует, что:
. Отсюда следует, что:
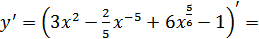
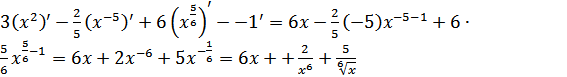 .
.
б) В этом случае имеем производную произведения. Согласно формуле 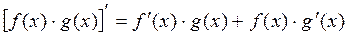 , получаем:
, получаем:
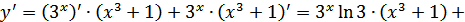
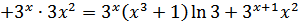 .
.
в) В этом случае имеем производную частного. Согласно формуле 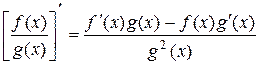 , получаем:
, получаем:
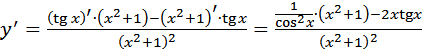 . Упростим полученное выражение. Получим:
. Упростим полученное выражение. Получим:
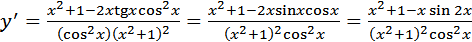 .
.
г) В этом случае имеем производную сложной функции. Для начала представим её в виде степени: 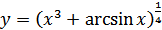 . Согласно правилу дифференцирования сложной функции, получаем:
. Согласно правилу дифференцирования сложной функции, получаем:
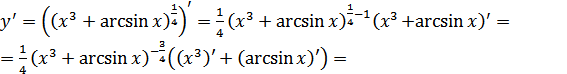
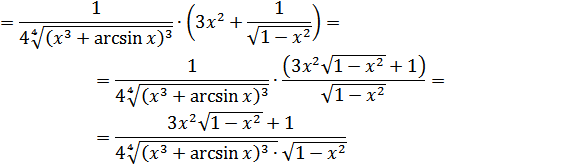
3. Исследовать данную функцию (т.е. найти точки экстремума и перегиба, интервалы возрастания, убывания, выпуклости и вогнутости графика функции) и построить ее графики.
1. 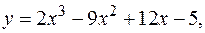
2. 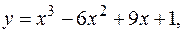
3. 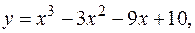
4. 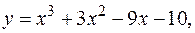
5. 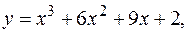
6. 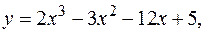
7. 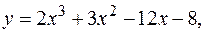
8. 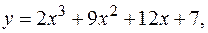
9. 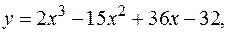
10. 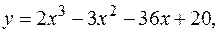
11. 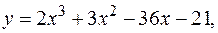
12. 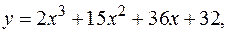
13. 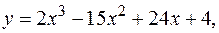
14. 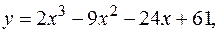
15. 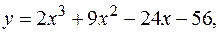
16. 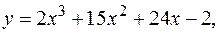
17. 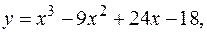
18. 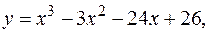
19. 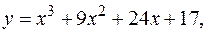
20. 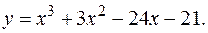
Решение типовой задачи
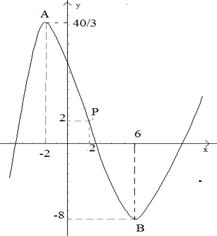
Исследовать на экстремум функцию 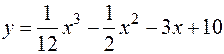 и определить интервалы ее возрастания и убывания, найти точки перегиба графика этой функции и определить интервалы выпуклости и вогнутости графика. Построить график.
и определить интервалы ее возрастания и убывания, найти точки перегиба графика этой функции и определить интервалы выпуклости и вогнутости графика. Построить график.
Решение.
Чтобы найти точки экстремума, вычисляем производную и приравниваем ее к нулю, решаем полученное уравнение:
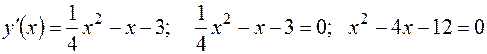
Корни уравнения 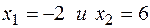 - критические точки. Эти точки разбивают числовую ось на три интервала:
- критические точки. Эти точки разбивают числовую ось на три интервала: 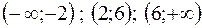 .
.
Производную 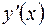 можно представить так:
можно представить так: 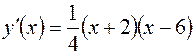 .
.
 Из последнего равенства видно, что в первом интервале
Из последнего равенства видно, что в первом интервале 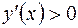 , во втором
, во втором 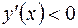 и в третьем интервале
и в третьем интервале 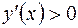 . Следовательно, в первом и третьем интервалах функция возрастает, а во втором убывает. Так как в критической точке
. Следовательно, в первом и третьем интервалах функция возрастает, а во втором убывает. Так как в критической точке 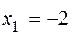 производная меняет знак с плюса на минус, то в этой точке функция имеет максимум. А в силу того, что в точке
производная меняет знак с плюса на минус, то в этой точке функция имеет максимум. А в силу того, что в точке 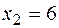 производная меняет знак с минуса на плюс, функция имеет минимум в этой точке. Вычислим значение функции в этих точках:
производная меняет знак с минуса на плюс, функция имеет минимум в этой точке. Вычислим значение функции в этих точках:
Рисунок 1
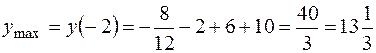 .
.
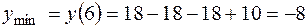
Точка B(6;-8)- точка минимума.
Точка A(-2;13 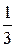 )- точка максимума.
)- точка максимума.
Чтобы найти точки перегиба, интервалы выпуклости и вогнутости, находим вторую производную, приравниваем ее нулю и решаем полученное уравнение.
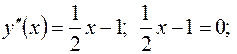
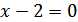 ;
; 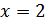 – критическая точка второго рода. Эта точка разбивает числовую ось на два интервала:
– критическая точка второго рода. Эта точка разбивает числовую ось на два интервала: 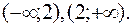
 Как видно, в первом случае
Как видно, в первом случае 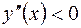 , во втором –
, во втором – 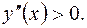 Следовательно, в первом интервале график функции – выпуклый, во втором – вогнутый. Так как производная
Следовательно, в первом интервале график функции – выпуклый, во втором – вогнутый. Так как производная 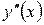 при переходе через точку х = 2 меняет свой знак, то х = 2 есть абсцисса точки перегиба графика. Вычисляем ординату этой точки:
при переходе через точку х = 2 меняет свой знак, то х = 2 есть абсцисса точки перегиба графика. Вычисляем ординату этой точки:
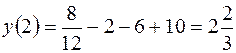 ;
;
Таким образом, точка 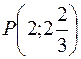 – точка перегиба графика функции.
– точка перегиба графика функции.
По результатам исследования строим график (см. рисунок 1).
6 В задачах 1-20 требуется найти указанные неопределенные интегралы:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
Решение типовых задач
а) Найти интеграл
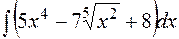
Решение:
Воспользуемся следующими свойствами неопределенного интеграла:
1. постоянной множитель можно выносить за знак интеграла, то есть
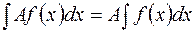
2. Неопределенный интеграл от суммы (разности) функций равен сумме (разности) интегралов от каждой функции в отдельности, то есть
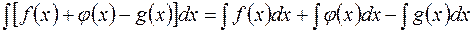
Преобразуем подынтегральную функцию в интеграле а) и воспользуемся формулой 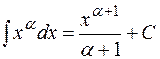 , где
, где 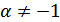 из таблицы основных неопределенных интегралов:
из таблицы основных неопределенных интегралов:
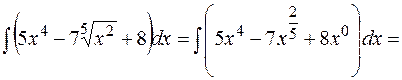
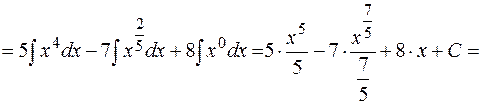
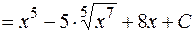
б) Найти интеграл
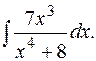
Решение:
Воспользуемся подстановкой 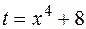 . Тогда
. Тогда 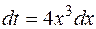 , откуда
, откуда 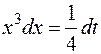 .Таким образом,
.Таким образом,
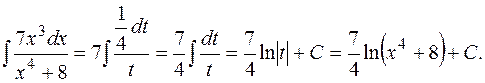
в) Найти интеграл
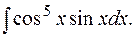
Решение:
Воспользуемся подстановкой 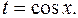
Тогда 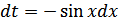 ;
; 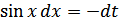 . Таким образом,
. Таким образом,
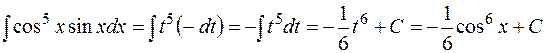
5. В задачах 1-20 вычислить площадь фигуры, ограниченной параболой и прямой. Сделать чертеж и заштриховать искомую площадь.
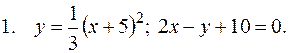
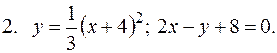
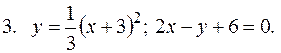
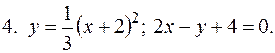
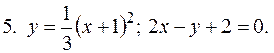
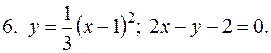
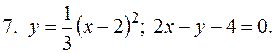
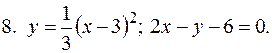
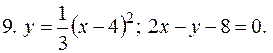
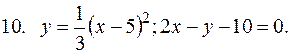
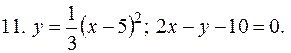
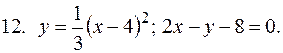
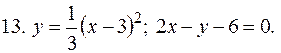
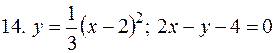
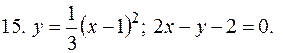
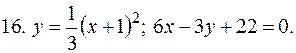
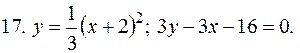
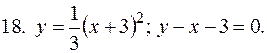
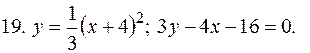
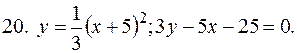
Решение типовой задачи
Вычислить площадь фигуры, ограниченной параболой
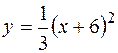 и прямой
и прямой 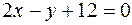 .
.
Решение:
Площадь фигуры, ограниченной сверху непрерывной кривой у = f (х), снизу непрерывной кривой 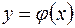 , слева прямой х = а, справа прямой х = b , вычисляется по формуле:
, слева прямой х = а, справа прямой х = b , вычисляется по формуле:
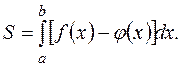 (1)
(1)
Если кривые у = f (х) и 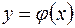 образуют замкнутую линию, то точки а и b совпадают с абсциссами точек пересечения этих кривых. Найдем точки пересечения заданных параболы и прямой. Для этого решим систему их уравнений:
образуют замкнутую линию, то точки а и b совпадают с абсциссами точек пересечения этих кривых. Найдем точки пересечения заданных параболы и прямой. Для этого решим систему их уравнений:
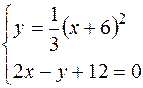
Приравняв значения у из обоих уравнений, получим:
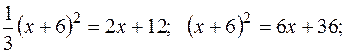
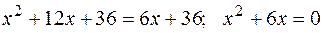
Отсюда 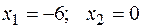 .Таким образом, парабола пересекается с прямой в точках А(-6;0) и В(0;12). Искомая фигура изображена на рисунке:
.Таким образом, парабола пересекается с прямой в точках А(-6;0) и В(0;12). Искомая фигура изображена на рисунке:
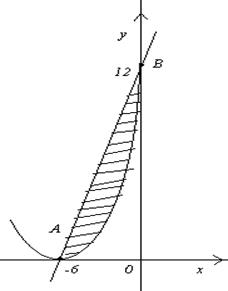
Из формулы (1) следует, что площадь фигуры равна
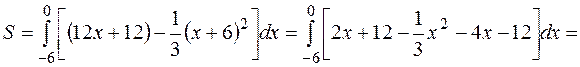
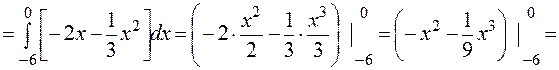
= 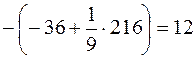 (кв. ед.)
(кв. ед.)
6. Решить задачи 1-20, используя основные теоремы теории вероятностей
1. В стаде 40% овец черного цвета. Найти вероятность того, что из двух наугад выбранных овец:
а) обе окажутся черного цвета;
б) хотя бы одна окажется черного цвета.
2. В стаде 60% овец черного цвета. Найти вероятность того, что из трех наугад выбранных овец:
а) только одна окажется черного цвета;
б) только две окажутся черного цвета.
3. На складе 70% досок хвойных пород. Найти вероятность того, что из трех наугад взятых досок:
а) все три окажутся из хвойных пород;
б) ни одной не будет хвойной породы.
4. Всхожесть зерна 90%. Найти вероятность того, что из трех наугад посеянных зерен взойдут:
а) только одно;
б) только два;
в) все три зерна.
5. Известно, что при посадке погибает 1/4 саженцев. Найти вероятность того, что из четырех посаженных саженцев приживутся:
а) все три;
б) только один;
в) хотя бы один саженец.
6. В некотором водоеме лещи составляют 70% от всего количества рыбы. Какова вероятность того, что из трех выловленных рыб окажется:
а) только один лещ;
б) все три леща.
7. Вывод поголовья цыплят в инкубаторе составляет в среднем 80%. Какова вероятность того, что из трех заложенных в инкубатор яиц выведется:
а) три цыпленка;
б) хотя бы один цыпленок.
8. Всхожесть семян гороха 60%. Найти вероятность того, что из наугад взятых четырех семян гороха взойдет:
а) хотя бы одно;
б) только одно.
9. В партии хлопка содержится 70% коротких волокон. Найти вероятность того, что из трех наугад взятых волокон:
а) все три окажутся короткими;
б) хотя бы одно окажется коротким;
в) ни одно не будет коротким.
10. Известно, что при посадке погибает 1/3 саженцев. Найти вероятность того, что из трех посаженных саженцев приживутся:
а) все три;
б) только один;
в) хотя бы один саженец.
11. Всхожесть семян данного растения составляет 90%. Найти вероятность того, что из четырех посеянных семян взойдут три.
12. Принимая вероятность рождения телочки и бычка одинаковыми, найти вероятность того, что среди 6 родившихся телят 4 бычка.
13. В хлопке число длинных волокон 80%. Какова вероятность того, что среди взятых наудачу 5 волокон окажется 3 длинных?
14. Доля витаминизированного комбикорма, поступившего на ферму составляет 10%. Какова вероятность того, что среди 4 мешков комбикорма, поступивших на ферму будет 2 мешка с витаминизированным комбикормом?
15. В некотором хозяйстве коров бестужевской породы составляют 70% от всего количества коров. Какова вероятность того, что из трех наугад взятых коров окажется:
а) хотя бы одна бестужевской породы;
б) все три бестужевской породы.
16. Вероятность того, что комбайн проработает в течении недели без поломок, равна 0,3. Какова вероятность того, что в звене из 4 комбайнов за неделю ремонта потребует 1 комбайн?
17. Вероятность того, что корова даст в день более 15 литров молока 0,7. Найти вероятность того, что из отобранных наугад 4 коров 2 дадут более 15 литров.
18. Среди хранящихся на складе доильных аппаратов 20% неисправных. Какова вероятность того, что из 6 взятых 3 аппарата окажутся исправными?
19. Всхожесть семян фасоли 60%. Найти вероятность того, что из наугад взятых четырех семян взойдет:
а) хотя бы одно;
б) все взойдут.
20. Всхожесть зерна 95%. Найти вероятность того, что из трех наугад посеянных зерен взойдут:
а) хотя бы одно;
б) только два;
в) все три зерна.
Решение типовой задачи
В стаде 65% коров бестужевской породы. Найти вероятность того, что из трех наугад выбранных коров окажется: а) все три бестужевской породы; б) только одна бестужевской породы; в) только две бестужевской породы; г) ни одной бестужевской породы; д) хотя бы одна бестужевской породы.
Решение.
Если в стаде 65% коров бестужевской породы, то это означает, что вероятность того, что случайно отобранная корова будет этой породы, равна р=0,65.
Вероятность противоположного события, т.е. того, что корова будет другой породы, равна q =1 - p =1 – 0,65=0,35 .
а) Вероятность того, что все три случайным образом отобранные коровы окажутся бестужевской породы, находится по теореме умножения независимых событий и будет равна:
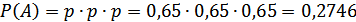 .
.
б) Вероятность того, что только одна из трех случайным образом отобранные коровы окажутся бестужевской породы, означает, что при этом две другие не бестужевской породы. Поэтому используем теорему умножения независимых событий. Так как таких ситуаций три, то получим:
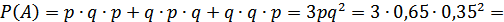
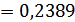 .
.
в) Вероятность того, что только две из трех случайным образом отобранные коровы окажутся бестужевской породы по аналогии с предыдущим случаем, находится по формуле:
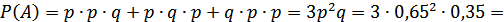
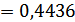 .
.
г) Вероятность того, что ни одна из трех случайным образом отобранные коровы окажутся бестужевской породы, найдем по теореме умножения независимых событий:
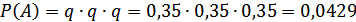 .
.
д) Вероятность того, что хотя бы одна из трех случайным образом отобранных коров окажется бестужевской породы, находится как разность между единицей и произведением вероятностей противоположного события.
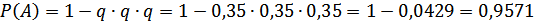 .
.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Шипачев В.С. Высшая математика: Учеб./под ред. А.Н. Тихонова. – 2-е изд. стереотип. – М.: Высш. шк., 1990. – 479 с.
2. Письменный Д.Т. Конспект лекций по высшей математике. первая, вторая части. –М.:Рольф, 2002. – 288 с.
3. Зайцев И. А. Высшая математика: Учеб. – М.: Высш. шк., 1991. – 400 с.
4. Данко П.Е. и др. Высшая математика в упражнениях и задачах: в двух частях – М.: Высш. шк. Т.1. – 1999. – 304 с.
5. Шипачев В.С. Задачник по высшей математике: Учеб. пособие. – 2-е изд., испр. – М.: Высш. шк., 2000. – 304 с.
Лицензия РБ на издательскую деятельность №0261 от 10 апреля 1998 года
Подписано в печать __________2006г. Формат . Бумага типографская. Гарнитура Таймс. Усл. печ. л.___. Усл. изд. л._____. Тираж____экз. Заказ №__.
Издательство Башкирского Государственного Аграрного Университета.
Типография Башкирского Государственного Аграрного Университета.
Адрес издательства и типографии: 450001, г. Уфа, ул. 50 лет Октября, 34.









