Занятие 10. 3 проверка надежности теста
Цель работы. Проверка надежности теста методом «тест-ретест» и методом расщепления «четное-нечетное», оценка плотности теста (консистенции).
Определение основных понятий. Надежность - характеристика теста, отражающая точность измерения и стабильность результатов. Количественно оценивается коэффициентом надежности
f = 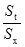 = 1 -
= 1 - 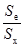 ,
,
где St - «истинная» дисперсия теста; Sх - эмпирическая дисперсия теста; Sе - дисперсия ошибки.
Прямая оценка коэффициента надежности невозможна (принципиально невозможно непосредственно определить St и Sе), поэтому применяют косвенные корреляционные методы, например метод «тест-ретест», метод расщепления.
Метод «тест-ретест» заключается в следующем: через некоторое время после первого проводится повторное тестирование с достаточным временным интервалом. Оценкой надежности служит коэффициент корреляции (Пирсона, ранговый или какой-либо иной, в зависимости от типа шкальных значений результатов тестирования).
Метод расщепления на части, в данной работе - на две части по принципу «четные-нечетные задания». В этом методе сопоставляются четные и нечетные номера заданий. Сила связи между этими двумя частями теста характеризует его надежность.
Возможно расщепление теста на любое количество частей. В предельном случае количество частей равно количеству заданий теста. Надежность в этом случае оценивается коэффициентом плотности (консистенции).
Математический аппарат
f = 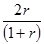 ; (1)
; (1)
f = 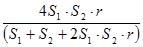 = d; (2)
= d; (2)
f = 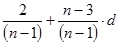 ; (3)
; (3)
f1 = 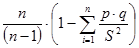 ; (4)
; (4)
где f - коэффициент надежности; r - коэффициент корреляции между двумя частями теста (Пирсона или ранговый); S1, S2 - среднеквадратичные отклонения 1-й и 2-й половин теста, соответственно; S1 = 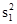 , S2 =
, S2 = 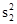 - дисперсии 1-й и 2-й половин теста, соответственно; п - количество заданий теста; d - символ для сокращения записи; f1 - коэффициент консистенции; S - дисперсия всех задач теста; р - индекс трудности задачи в десятичной дроби (1/100); q = 1- р.
- дисперсии 1-й и 2-й половин теста, соответственно; п - количество заданий теста; d - символ для сокращения записи; f1 - коэффициент консистенции; S - дисперсия всех задач теста; р - индекс трудности задачи в десятичной дроби (1/100); q = 1- р.
Значение коэффициента надежности теста редко превышает на практике 8.
Тест считается надежным при f > 6.
- Формула Спирмена-Брауна (1). Применяется, если дисперсии обеих частей теста равны. Это предположение проверяется с помощью критерия Фишера: F = S1/ S2 если эмпирическая статистика F превышает табличное значение Ft,то гипотезу о равенстве дисперсий следует отклонить. В данном случае при 21 степени свободы, для уровня значимости 0,05 Ft = 2,1.
- Формула Флангана (2). Применяется в случае неравенства дисперсий.
- Формула Кристофа (3). Применяется в случае малого количества заданий теста (п<50).
- Формула Кьюдера - Ричардсона (4). Частный случай формулы Кронбаха для дихотомических интерпретаций ответов «правильно-неправильно».
Порядок работы. Студентам предлагается тест «Домино», с которым они работали на прошлом занятии.
Обработка данных
1.Составляется таблица (табл. 10.3.1), где Х1i - количество правильно решенных задач i-м испытуемым - показатель успешности работы i-го испытуемого в 1-м тестировании; Х2i-показатель успешности работы i-го испытуемого во 2-м; N - объем выборки испытуемых.
Таблица 10.3.1
Определение надежности методом «тест-ретест»
| i | X1 | X2 |
| 1 | ||
| … | ||
| N |
Вычисляется коэффициент корреляции r (Х1, X2).
2. Задания теста (после повторного тестирования) разбиваются на четные и нечетные. Составляется таблица (табл. 10.3.2), где У1i, У2i - количество испытуемых, правильно решивших соответствующую задачу; п - количество задач.
Таблица 10.3.2
Определение надежности методом расщепления
| i | Y1 | Y2 |
| 1 | ||
| … | ||
| п /2 |
Для каждого столбца вычисляются средние, дисперсии и корреляция между столбцами.
- Проверяется условие применения формулы (1). Вычисляется f.
- Вычисляется f по формуле (2).
- Вычисляется f по формуле (3).
3. Составляется таблица (табл. 10.3.3), где р=Х i /N; q= l- p; N –количество испытуемых.
Таблица 10.3.3
Таблица результатов
| i | Х | р | q |
| 1 | |||
| … | |||
| N |
- Вычисляется f1.
Анализ результатов. Сравнивая значения f, полученные различными способами, студенты проверяют, насколько способ вычисления влияет на результат, насколько существенно требование равенства дисперсий, насколько оценка коэффициента надежности чувствительна к количеству заданий теста.
Выводы. Делается вывод о ретестовой надежности теста, надежности расщепления, плотности; насколько эти показатели отличаются друг от друга.
Занятие 10.4 СТАНДАРТИЗАЦИЯ ТЕСТА
Цель работы. Построение шкал теста на основе полученных «сырых» оценок.
Определение основных понятий. Стандартизация - приведение оценок теста к виду, сопоставимому с результатами других методик, измеряющих данный признак. Чаще всего это достигается или построением шкал процентилей, или шкал, основанных на z-оценках.
Шкала процентилей - разбиение выборки испытуемых на заданное число частей. Опираясь на кумулятивную кривую, процентильное шкальное значение показывает, какая часть выборки испытуемых обладает значением признака, не превосходящим заданное, т. е. с какой вероятностью можно ожидать такие значения признака.
Алгоритм построения шкалы. Проверяется гипотеза о нормальном распределении.
Если гипотеза не отклонена, то следовательно область изменения вероятности [0,1] разбивается на заданное число частей (4 части - шкала квартилей, 10 частей - шкала децилей, 100 частей - шкала собственно процентилей).
По таблице нормального распределения для границ разбиения находится соответствующий квантиль. Этот квантиль является искомым шкальным значением.
Z-оценки - выражение шкальных значений в единицах стандартного отклонения (среднеквадратичного отклонения).
При выполнении условия нормального распределения оценок, шкалы, основанные на z-оценках, являются шкалами интервалами. Линейное преобразование, допустимое для шкал интервалов, позволяет привести их к удобному виду:
S = А + В ´ Z,
здесь А - позволяет сдвинуть начало отсчета и освободиться от отрицательных шкальных значений, множитель В изменяет масштаб, что позволяет перейти от дробных к целым шкальным значениям.
Z-оценка может быть получена линейным преобразованием:
где х - непреобразованная тестовая оценка; М - оценка математического ожидания (среднее арифметическое); s - оценка среднеквадратичного отклонения; т. е. z-оценка путем центрирования (сдвига точки отсчета в 0) и нормирования (переход к единицам среднеквадратичного отклонения).
Если известна вероятность того, что величина признака не превосходит некоторое значение, то 2-оценка будет равна квантилю этой вероятности и может быть найдена из таблицы нормального распределения.
Математический аппарат. Критерии проверки гипотезы о нормальном распределении.
При выборках объемом больше 50 рекомендуется применять критерий c2.
Порядок работы. Даны результаты обследования группы испытуемых (N = 63) с помощью теста Айзенка (см. прил. 10.4.1). Для каждого из показателей (экстраверсии и нейротизма) следует:
1. Построить гистограмму распределения частот. Проверить гипотезу о нормальном распределении с помощью критерия c2.
2. Построить кривую накопленных частот (кумуляту).
3. Построить процентильную шкалу децилей.
4. Построить z-шкалу.
5. С помощью коэффициента корреляции Пирсона проверить гипотезу о статистической независимости показателей нейротизма и интроверсии.
Анализ результатов. Из свойств нормального распределения следует, что для показателей теста Айзенка
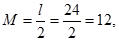
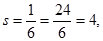
где М - математическое ожидание, l - размах, s - среднеквадратичное отклонение.
Сравните полученные вами оценки с теоретическими.
Приложение 1 0.4. 1
Показатель экстраверсии:
4;12;10; 9;14;10; 8; 7; 12; 7;13;17;13; 12;14; 15;18;17; 5; 7;15;12;16; 8;15; 10; 11; 8; 14; 13; 12; 8; 13; 14; 8; 4; 13; 4; 10; 12; 6; 12; 14; 10; 11; 9; 9; 16; 17; 19;10;20;16;11;11;20; 9;11;13; 8;11;11; 6.
Показатель нейротизма:
10; 11; 19; 14; 9:20; 7; 20; 20; 19; 9; 7; 10; 14; 18; 13; 11; 15; 9; 11; 13; 19: 17; 19; 16; 8;21;17;16; 5; 16; 15; 13; 21; 14; 10; 4; 19; 12; 20; 21; 16: 21; 7;12;11; 4;13; 13; 6;12;16;23;19;15;17;11; 4;13;22;20;15;15.








