57 Дифференциальные уравнения
Для АСРn-го порядка и любого элемента n-го порядка АСР в общем виде ДУ имеет вид:
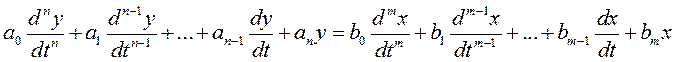у - выходная переменная АСР, х - входная, dt - динамика АСР. Для решения уравнения применяют операционное исчисление основанные на преобразовании по Лапласу.
Преобразование Лапласа имеет следующий вид
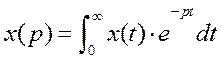гдеx(t)- аргумент, x(p)- изображение данного аргумента (изображение сигнала, т.е. преобразованное по Лапласу значение) , p- некоторая комплексная переменная, которая называется переменная Лапласа
Свойства преобразования при начальных нулевых значениях т.е. t=0 x(t)=0
1) 
, 
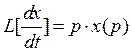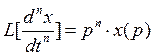, 9
2) 
,
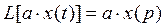3) 
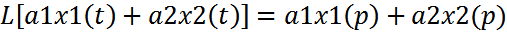
4) 
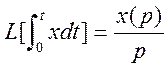, где L-преобразование
58. Передаточные функции
Преобразование по Лапласу с использованием его свойств :
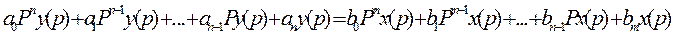- это ур-е операторной формы
Затем выносим общее за скобки:
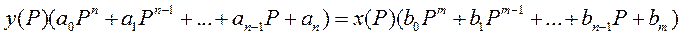
возьмем отношение :
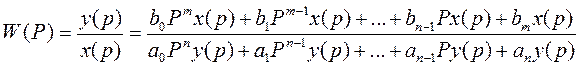-это передаточная ф-ция АСР
Отношение преобразуем по Лапласу выходной величины АСР или линейно к преобразованной по Лапласу входной величины элемента называется передаточной функцией АСР или элемента. Знаменатель передаточной функции = 0, называется характеристическим уравнением АСР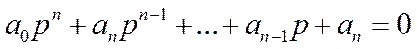 
59. Уравнения типовых звеньев АСР. Назначение и классификация типовых звеньев
Любая АСР состоит из отдельных элементов или звеньев объединенных в схему( Х У ) при этом динамическая характеристика АСР зависит из динамических характеристик звеньев и способов их соединения. Динамическая характеристика отдельных звеньев и АСР в целом используется для анализа работы АСР в переходном режиме, который является основным, т.к. АСР в промышленных условиях и ее объект регулирования постоянно подвержены возмущающему воздействию. Поэтому для получения динамических характеристик всей АСР нужно знать характеристики всех ее элементов. Объектов регулирования, датчиков, регуляторов и др.
Динамической характеристикой АСР называют зависимость выходной переменной (у) от входной переменной (х) и функцией времени.
у=f(х,t)
Все элементы АСР по своим динамическим характеристикам, т.е по зависимости выходной величины можно классифицировать на следующие типовые звенья:
– безинерционные (усилительные);
– инерционные (аппериодическое звено 1-го порядка);
– интегрирующая(астатическое звено 1-го порядка);
– дифференцирующие звенья;
– колебательно затухающее звено;
– аппериодическое звено 2-го порядка;
– звено чистого запаздывания.
60. Безинерционное звено
Безынерционным или усилительным звеном называют звено, в котором выходная величина воспроизводит без искажений и запаздываний входную величину.
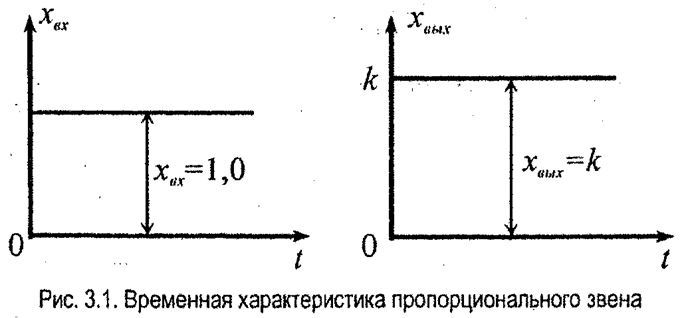
Связь между выходом и входом звена определяется алгебраическим уравнением вида
,
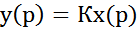где k - коэффициент пропорциональности, называемый обычно коэффициентом передачи (усиления) звена.
Передаточная функция безынерционного звена
.
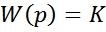Пример данного звена- П-регулятор, электрические усилители, различные редукторы (механические).
61. Инерционное звено
Динамическая характеристика такого звена имеет вид:
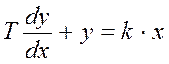
T - постоянное времени, к - коэффициент усиления.
x-const;
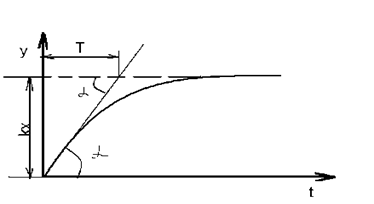
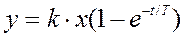
Для этого (3.2.3) преобразуем по Лапласу:
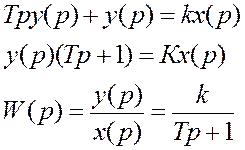
Используется в одноемкостных статических объектах: термопары, мембрано-исполнительный механизм. Данное звено называется аппериодическим звеном 1-го порядка.
62. Интегрирующее звено
Динамическая характеристика: Т*dy/dt=к*х
Преобразуем: dy/dt=к*х/Т,
,
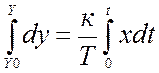Проинтегрируем: y-y0=(к*х/Т)*t,
х=cоnst,
y=(кх/Т)*t+y0
График переходного процесса:
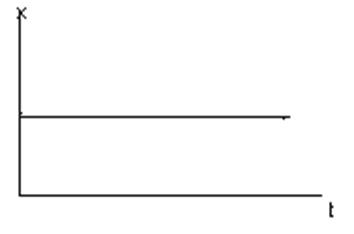
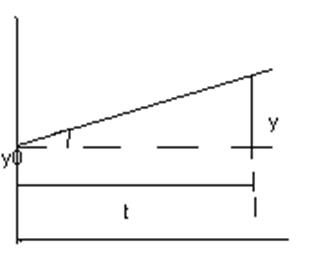
Получим функцию звена, преобразуем по Лапласу:
Т*р*y(р)=к*х(р), W(р)=y(р)/х(р)=к/Т*р. Данное звено называется астатическим звеном 1-го порядка
Используются в емкостных астатических объектах, интегральных регуляторах).
63. Дифференцирующие звенья
Они делятся на реальные и идеальные.
а) Идеальное дифференц.звено.
Динамическая характеристика имеет вид:
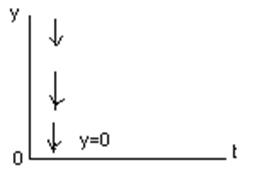
y=к*dх/dt (При t=0, y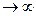 
; при t 
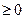, у=0)
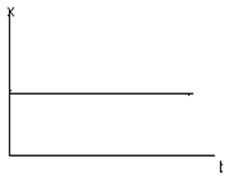
Получим передаточную функцию звена: у(р)=к*р*х(р), W(р)=у(р)/х(р)=к*р
Пример:
1. Электрический контур, в котором протекает ток и имеется напряжение, тогда ток в контуре будет равен: 
i=c*dUвых/dt
2. Трансформеры напряжения: Uвых = к*dФ/dt, Ф=к1*l1 (величина потока создается в сердечнике l1). Uвых=K2*dl1/dt (выходное напряжение).
б) реальное дифференц.звено
Динамическая характеристика имеет вид: Т*dy/dt + y = k*dx/dt (при t=0, y 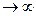, при t 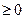, y=k*x*e-t/T
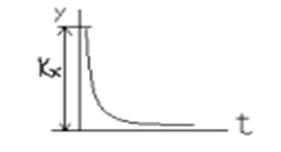
Получим передаточную функцию данного числа и преобразовываем по Лапласу: Т*р*у(р) + у(р)=к*р*х(р), W(р)=к*р/(Т*р+1).
Пример: электрический контур, содержащий емкость С и сопротивление R. Получим: R*c*dUвых/dt + Uвых = c*dUвых/dt – закон Киркгофа. Дифференцирующие звенья широко применяются в АСР и способствует устойчивой ее работе.
64. Колебательное затухающее звено, апериодическое звено 2-го порядка
65. Звено чистого запаздывания
Динамическая его характеристика имеет вид:
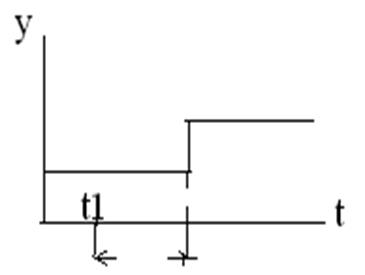у = х*(t – τ), где τ – время запаздывания между изменениемвходной величины относительно выходной. График переходного процесса: (график один под другим, чтобы совпадали t1)
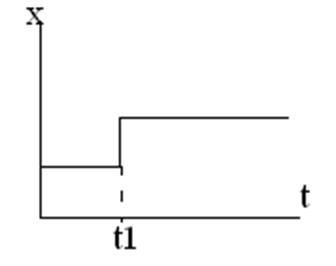В момент времени t1 увеличивается значение х. Через время τ на данную величину изменилось значение выходной величины на такую же величину.
Передаточная функция имеет вид: W(р)=у(р)/х(р)=е-р*τ