40. Классификация систем автоматического регулирования

Дата: 2025-05-21; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

1.По виду воздействующего воздействия :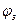

Стабилизирующая в которой 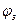=const

Программные АСР, где 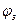изменяется по заданной временной программе =

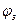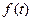
Следящие АСР, где величина 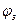изменяется в соответствии с изменением какой либо др. величиной

Оптимизирующая АСР, где величина 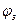вырабатывается на оптимальном уровне и поддерживается на этом уровне с одним регулятором.

2.По принципу действия: а) Аср по отклонению

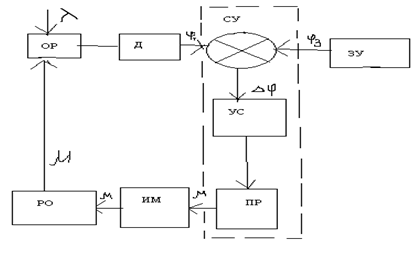Б) АСР по возмущению.

АСР по отклонению: обязательно присутствует ошибка регулирования ∆φ и только тогда АСР оказывает регулирующее воздействие с целью компенсации ∆φ (недостаток). Достоинство: ∆φ следствие действия на ОР практически всех возможных возмущающих воздействий (даже неконтролируемых).

АСР по возмущению.В этих АСР компенсируется только одно возмущ. воздействие которое появляется на выходе объекта регулирования и этот процесс препятствует появлению .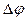

Достоинство:Сравнительная быстрота воздействия на объект регулирования что вызывает улучшение качества процесса регулирования.

Недостатки:Если на объект действует много возмущений то 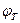будет иметь значительное отклонение , поэтому в наиболее ответственных случаях применяют комбинированные АСР которые реализуются по возмущению и отклонению.

41. Объекты регулирования

От свойств ОР зависит характер работы всей АСР. В частности, для выбора типа регулятора АСР и определения параметров его настроек необходимо определить динамическую характеристику ОР.

Динамическая характеристика ОР — изменение во времени регулируемой величины выходного параметра объекта (функции времени) при изменении входной величины.

φ=f(t) μ=const

В химической технологии ОР классифицируют по:

1) Физико-химическим процессам

2) Конструктивному оформлению

3) Температурному режиму

4) Структуре потоков и т.д.

По динамическим характеристикам:

1 одноемкостные статические объекты

2 одноемкостные астатические объекты

3 объекты чистого запаздывания

4 двухемкостные статические объекты

5 двухемкостные астатические объекты

42.Одноемкостные статические объекты.

Емкость – способность объекта запасать материальную и тепловую энергию.

Статическими называются объекты регулирования, у которых при изменении входной величины после окончания переходного процесса в установившемся режиме работы объекта формируются установившееся значение выходной или регулируемой величины. При этом регулируемая величина влияет на значениевходной величины, т.е. данные объекты обладают свойством самовыравнивания.

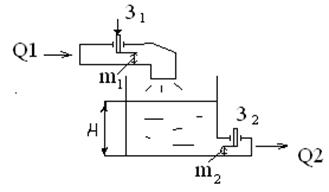
На притоке жидкости установлена задвижка З₁ в положении m_1, величина потока на входе Q₁.На стоке установлена задвижка З₂ в положении m_2, величина потока на входе Q₂. В установившемся режиме Q₁=Q₂ Увеличение закрытия З₁ до значенияm₁‘>m₁, тогда Q₁’>Q₁, при этом увеличится уровень в резервуаре и увеличивается гидростатический уровень в нем, величина Q₂’>Q₂ и уровень Н’₁=соnst, но Н’₁>H. Изменение уровня описывается уравнением: 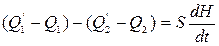; Рассмотри относительное изменение Q1 отm1:

; ;

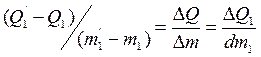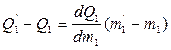Рассмотрим относительное изменение Q2 от Н:

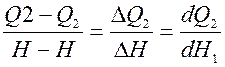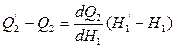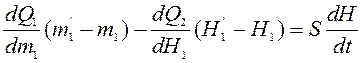; ; — динамическая характеристика данного резервуара как ОР уровня при регулировании на входе и самовыравнивании на стоке.

для получения уравнения в общем виде необходимо все величины записать в относительных единицах. 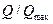, , 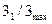, 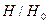получаем 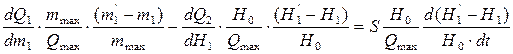, учитывая что 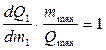, характеристика т.к. З₁ линейна , ,

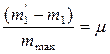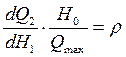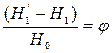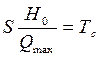, , окончательный вид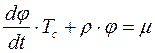

43. Одноемкостные астатические объекты

Астатический — объект, у которого при изменении входящей величины (регулирующего воздействия), выходящая величина (регулируемая величина) изменяется с постоянной скоростью не приходя к новому установленному значению.

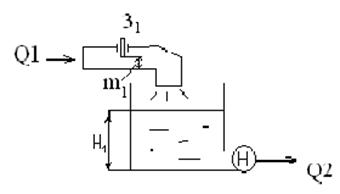Примером является резервуар, в котором регулируется уровень жидкости, при этом на стоке устанавливается насос постоянной производительности, на входе РО.

Q₂=соnst, предполагаем что m₁‘>m₁, при этом Q₁’>Q₁ значит Н₁ начнет увеличиватся. Данный объект не обладает свойством самовыравнивания, для получения его динамической характеристики используем уравнение для статического объекта:

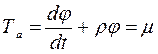, пусть ρ=0: 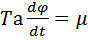–динамическая характеристика, Решим данное уравнение: 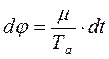, интегрируем 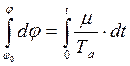, принимаем 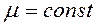, получаем ,

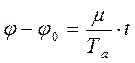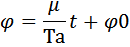
φ0— установившееся значение регулируемой величины.

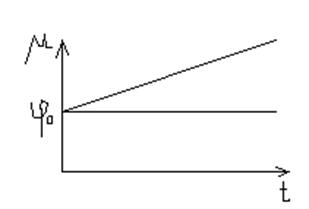
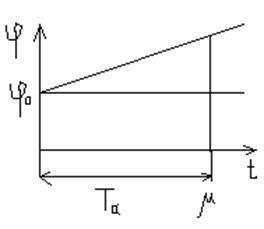Если t=Taтогда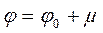

Та — время, за которое φ станет равным μ.

44. Объекты чистого запаздывания

Пример: конвейер, перемещающий сыпучий материал из бункера в аппарат.

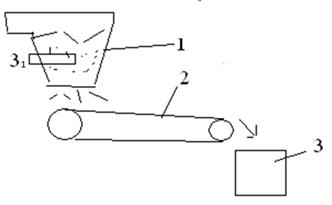1 – исходный бункер

2 – конвейер, рабочая длина l, лента перемещается с линейной скоростью

3 – приемный бункер

З₁ – заслонка

В исходном бункере находится заслонка З и степень открытия m определяет расход данного материала на конвейер.

µ - относительное изменение положения задвижки З и относительное регулирующее воздействие на входе.