Если на вход звена подать единичную функцию от времени 1[t] при нулевых начальных условиях системы, то реакция на выходе будет называться переходной функцией, которую обозначают h(t).
1. Что называют моделью, моделированием, инструментом, технологией, средой в моделировании?
Модель – есть создаваемый с целью получения и (или) хранения информации специфический объект, отражающий свойства, характеристики и связи объекта-оригинала, существенные для решаемой задачи. Моделирование – способ замещения реального объекта его аналогом.
План действий при построении модели:
· сформулировать цели получения системы (задачи);
· выбрать факторы и переменные, которые наиболее существенны для данной задачи;
· учесть каким-либо способом посторонние, не включенные в модель, факторы;
· осуществить оценку результатов, проверку модели, оценку полноты модели;
Инструмент – типовое средство, позволяющее достичь результата и обеспечивающее сокращение затрат на выполнение промежуточных операций.
Технология – набор стандартных способов, методов, позволяющих достичь результата гарантированного качества с помощью инструментов за известное время при заданных затратах, при соблюдении пользователем объявленных требований и порядка.
Среда – совокупность рабочего пространства и инструментов, поддерживающее хранение и изменение, преемственность проектов и интерпретирующая свойства объектов и систем из них.
2. Классификация моделей и моделирования.
Могут принимать форму: феноменологический и абстрактные, активные и пассивные, статические и динамические, дискретные и непрерывные, детерминированные и стохастические, функциональные и объектные; распределенные, структурные, сосредоточенные.
Феноменологические модели сильно привязаны к конкретному явлению, передает внешнее подобие.
Абстрактная модель воспроизводит систему с точки зрения её внутреннего устройства, копирует её более точно.
Пассивные модели выдают ответ на вопрос пользователя, когда тот об этом попросит.
Активные взаимодействуют с пользователем. Могут сами активировать диалог, менять его линию, имеют собственные цели. Все это происходит за счет того, что они могут самоизменяться.
Статические модели описывают явления без развития.
Динамические прослеживают поведение систем, поэтому используют в своей записи, например, дифференциальные уравнения, производные от времени.
Дискретные модели изменяют состояние переменных скачком, потому что не имеют детального описания связи причин и следствия, часть процесса скрыта от исследователя.
Непрерывные модели содержат информацию о деталях перехода переменных в иные состояния.
Детерминированные модели отображают точную связь между причиной и следствием.
Стохастические модели строятся с использованием понятия вероятности, т.к. из-за не изученности деталей не удается точно описать связь причин и следствия, возможно только описание в целом.
Если описание модели идет с точки зрения поведения, то модель функциональная. Если описание каждого объекта отделено от описания другого элемента объекта, то модель объектно-ориентированная.
Если каждый параметр, описывающий свойства объекта, в любых его точках имеет одинаковое значение (хотя может меняться во времени), то модель с сосредоточенными параметрами. Если параметр, в разных точках имеет разные значения, то он распределен и модель является распределенной. Иногда модель копирует структуру объекта, параметры объекта сосредоточены (объединены), то модель – структурная.
3. Регрессионные модели. Черный ящик, имеющий один вход и один выход.
Задача является регрессионной, если дано множество значений на входе и выходе, и надо построить модель, т.е. определить функцию ящика, по которой вход преобразуется в выход.
Решение задачи состоит из 3х этапов: вносится гипотеза о структуре ящика, строится функция зависимости и проверяется соответствие построенной функции экспериментальным данным.
К черному ящику, имеющему один вход и один выход, относятся следующие модели:
· Линейная модель Y=A1X+A0
· Степенная модель Y(x,a,m)=axm
· Показательная модель Y(x,a,m)=aexm
· Логарифмическая функция Y(x,a,b)=a*ln(x)+b
· Обратная линейная функция Y(x,a,b)=1/(a*x+b)
· Приближенная функция Y(x,a,b)=a*(1/x)+b
Все модели приводятся к линейной модели и решаются далее аналогично линейной.
4. Регрессионные модели. Черный ящик, имеющий несколько входом и один выход.
К черному ящику, имеющему несколько входов и один выход, относятся следующие модели:
· Линейная множественная модель Y=A0+A1X1+…+AmXm
· Полиномиальная множественная регрессионная модель, Y=A0+A1X1+A2X2+A3X1X2+A4X1X1+A5X2X2
· Мультипликативная (степенная) регрессионная модель Y=A0X1A1X2A2...XmAm
· Обратная регрессионная множественная модель Y=k/(A0+A1X1+…+AmXm)
· Экспоненциальная множественная модель Y=eB0+B1X1+…+BmXm
Все модели приводятся к линейной множественной модели и решаются далее аналогично линейной.
5. Динамические системы. Звено первого порядка.
Если в системе каждый раз значения на выходе, при одном и том же входном значении, разное, то есть зависит от того, в какой последовательности подавались входные значения, то это динамическая система.
Динамические системы, в отличии от статических, помнят свое прошлое состояние, то есть обладают памятью. В записи модели динамических систем присутствует производная, связывающая прошлое состояние системы с настоящим. Чем большей памятью обладает система, тем больше состояний из прошлого влияют на настоящее, тем большая степень старшей производной используется в записи модели.
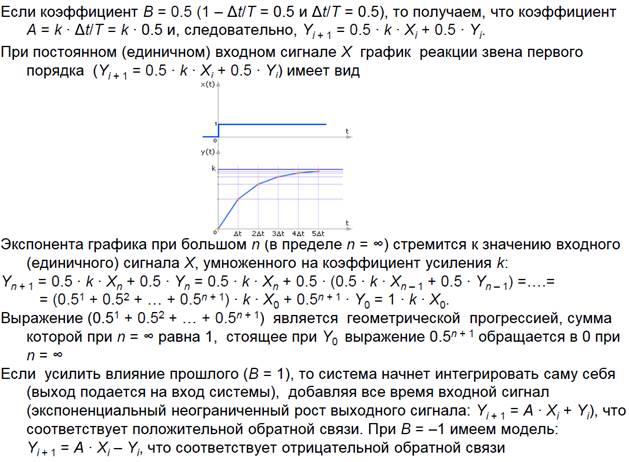
Если в системе каждый раз значение на выходе, при одном и том же входном значении, разное, то есть зависит от того, в какой последовательности подавались входные значения, то это динамическая система.
Динамические системы, в отличие от статических, помнят свое прошлое состояние, то есть обладают памятью. В записи модели динамических систем присутствует производная, связывающая прошлое состояние системы с настоящим. Чем большей памятью обладает система, тем больше состояний из прошлого влияют на настоящее, тем большая степень старшей производной используется в записи модели.
Звенья второго порядка описываются дифференциальным уравнением вида:
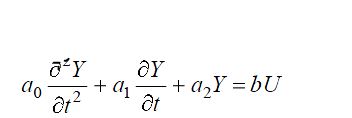
Если на вход звена подать единичную функцию от времени 1[t] при нулевых начальных условиях системы, то реакция на выходе будет называться переходной функцией, которую обозначают h(t).
Преобразуем по Лапласу уравнение звена второго порядка :
a0·p2·Y(t)+a1·p·Y(t)+a2·Y(t)=b·U(t)
(a0·p2+a1·p+a2)·Y(t)=b·U(t).
(Общая информация для вопросов 6-8)
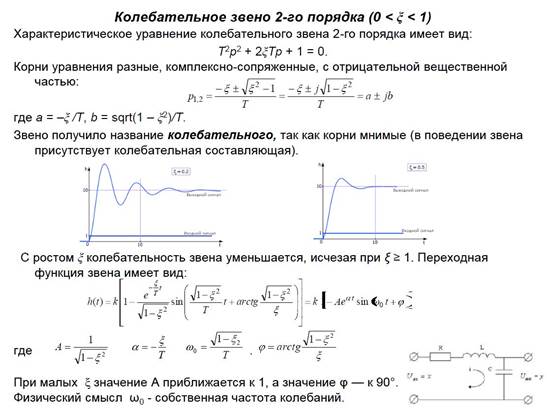
6. Динамические системы. Звенья второго порядка (колебательное звено).
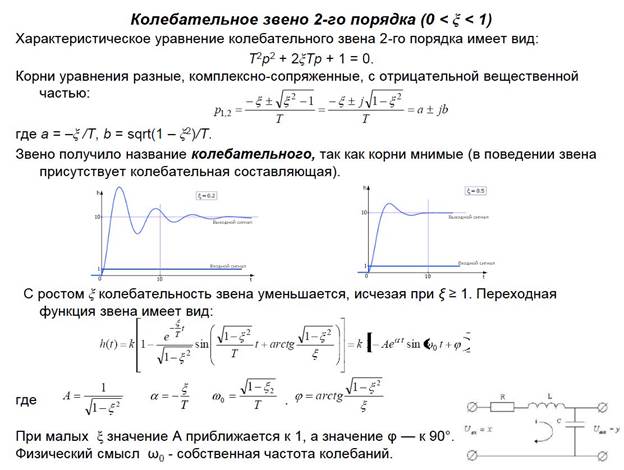
7. Динамические системы. Звенья второго порядка (апериодическое звено).
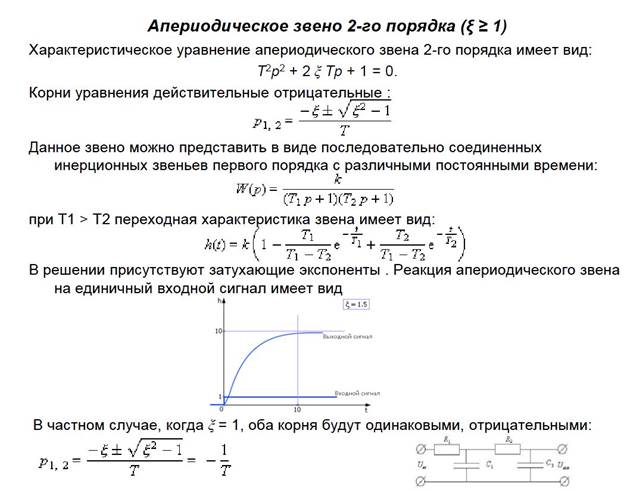
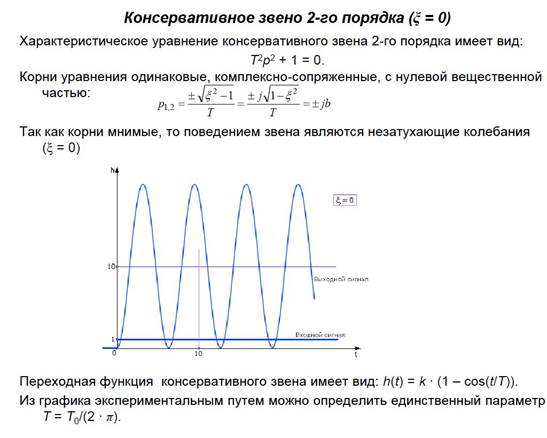
8. Динамические системы. Звенья второго порядка (колебательное, консервативное звено).
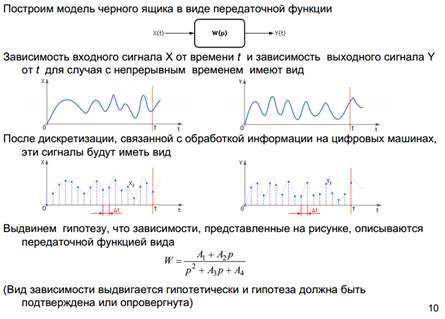
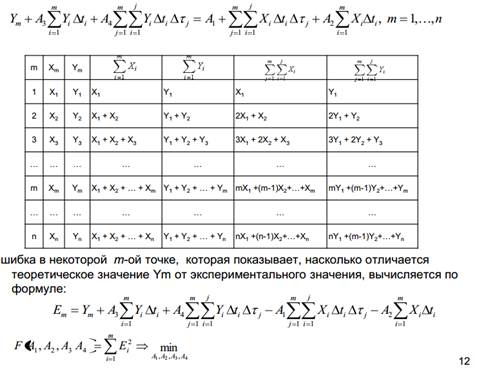
9. Динамические регрессионные модели, заданные в виде передаточной функции
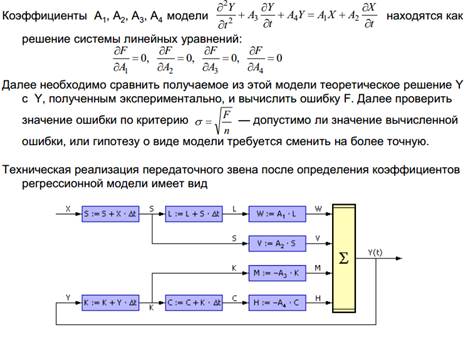
10. Корреляция
11. Использование метода Монте-Карло при исследовании систем со случайными параметрами
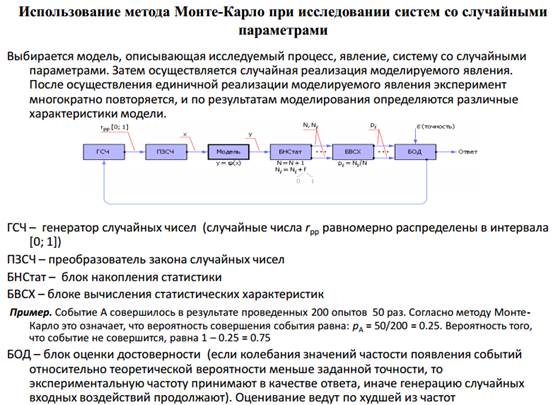
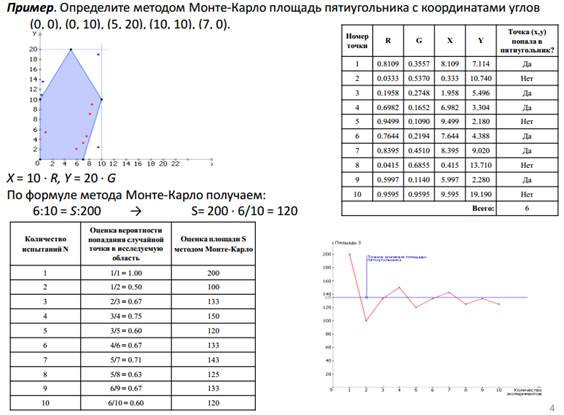
12. Нормальное распределение. Моделирование нормально распределенных случайных величин (табличный метод, метод Мюллера)
13. Нормальное распределение. Моделирование нормально распределенных случайных величин (метод, использующий центральную предельную теорему)
14. Биноминальное распределение случайных чисел
15. Распределение Пуассона случайных чисел 
16. Моделирование случайного события. Моделирование системы зависимых случайных величин и несовместных событий.
Случайным называют событие, которое в результате испытания может наступить, а может и не наступить (в отличие от достоверного события, которое при реализации данного комплекса наступает всегда, и невозможного события, которое при реализации данного комплекса условий не наступает никогда). Исчерпывающей характеристикой случайного события является вероятность его наступления. Примерами случайных событий являются отказы в экономических системах, объемы выпускаемой продукции каждым предприятием в каждый день, котировки валют в обменных пунктах, состояние рынка ценных бумаг и биржевого дела и т.п.
Моделирование случайного события заключается в определении («розыгрыше») факта его наступления.
Для моделирования случайного события А, наступающего в опыте с вероятностью РА, достаточно одного случайного (псевдослучайного) числа R, равномерно распределенного на интервале [0; 1]. В случае попадания ПСЧ R в интервал [0; РА], событие А считают наступившим в данном опыте, в противном случае — не наступившим в данном опыте. Чем больше вероятность наступления моделируемого события, тем чаще ПСЧ, равномерно распределенные на интервале [0; 1], будут попадать в интервал [0; РА], что и означает факт наступления события в испытании.
Для моделирования одного из полной группы JV случайных несовместных событий А1, А2, ..., AN с вероятностями наступления соответственно, также достаточно одного ПСЧ R.
Факт наступления одного из событий группы определяют, исходя из условия принадлежности ПСЧ R тому или иному интервалу, на который разбивают интервал [0; 1].
В практике имитационных исследований часто возникает необходимость моделирования зависимых событий, для которых вероятность наступления одного события оказывается зависящей от того, наступило или не наступило другое событие. В качестве одного из примеров зависимых событий приведем доставку груза потребителю в двух случаях: 1) когда маршрут движения известен и был поставщиком дополнительно уточнен, 2) когда уточнения движения груза не проводилось. Понятно, что вероятность доставки груза от поставщика к потребителю для приведенных случаев будет различной.
Существуют два алгоритма моделирования зависимых событий. Один из них условно можно назвать «последовательным моделированием», другой — «моделированием после предварительных расчетов».
17. Поток случайных событий. Поток Пуассона.
Когда событий много и они следуют друг за другом, то они образуют поток. Заметим, что события при этом должны быть однородными, то есть похожими чем-то друг на друга. Например, появление водителей на АЗС, желающих заправить свой автомобиль. То есть, однородные события образуют некий ряд. При этом считается, что статистическая характеристика этого явления (интенсивность потока событий) задана. Интенсивность потока событий указывает, сколько в среднем происходит таких событий за единицу времени. Но когда именно произойдет каждое конкретное событие надо определить методами моделирования. Важно, что, когда мы сгенерируем, например, за 200 часов 1000 событий, их количество будет равно примерно величине средней интенсивности появления событий 1000/200 = 5 событий в час, что является статистической величиной, характеризующей этот поток в целом.
Случайные потоки бывают:
ординарные: вероятность одновременного появления двух и более событий равна нулю;
стационарные: частота появления событий λ(t) = const(t);
без последействия: вероятность появления случайного события не зависит от момента совершения предыдущих событий.
За эталон потока в моделировании принято брать пуассоновский поток.
Пуассоновский поток — это ординарный поток без последействия.
Вероятность того, что за интервал времени (t0,t0+τ) произойдет m событий, определяется из закона Пуассона
 |
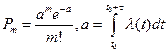Если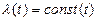 
-стационарный поток
Для простейшего потока (стационарного) вероятность того, что за время t произойдет m событий, определяется из закона Пуассона:
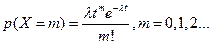
где λ - параметр распределения.
18. Поток случайных событий. Потоки Эрланга.
Про поток случайных событий в вопросе №17
Поток Эрланга k-го порядка — это поток случайных событий, получающийся, если в простейшем случайном потоке сохранить каждое k-е событие, а остальные отбросить. Порядок потока — мера последействия потока. То есть обратной величиной к мере случайности потока является его порядок.
λk = λ/k — интенсивность потока Эрланга k-го порядка, где λ — интенсивность простейшего потока Пуассона, а λk интенсивность просеянного k раз потока, то есть в k раз меньше.
Параметры закона Эрланга вычисляются по формулам: Mk = 1/λk, σk = 1/sqrt(k)/λk
Обратите внимание, что в потоке Эрланга M ≠ σ, то есть в потоках с последействием равенство M и σ невозможно.
Более того, при k –> ∞ событие происходит строго в размеренное время, так как σ –> 0.
Поток Эрланга 1-го порядка: m = σ1 — поток без последействия;
Поток Эрланга i-го порядка: m ≠ σ2, при этом (σ2 > 0) и (σ1 > σ2) разброс уменьшается, последействие увеличивается;
Поток Эрланга ∞-го порядка: m ≠ σ = 0 — регулярный поток.
Из этого следует, что порядок потока Эрланга — есть мера последействия потока.
Пример. Рассмотрим пример выхода из строя лампочек на опоре уличного освещения. Примем время наблюдения 100 лет. Из паспортных данных на эти изделия известно, что среднее время работы изделия на отказ составляет 1.5 года; среднеквадратическое отклонение — 0.5 года.
То есть, задано: Mk = 1.5, σk = 0.5.
Поскольку Mk ≠ σk, то k ≠ 1, то есть мы имеем дело с потоком с последействием. Интенсивность этого потока λk = 1/Mk = 1/1.5 = 0.67. Вычисленная интенсивность потока говорит нам о том, что в течение года в среднем перегорает 0.67 лампочки или 67 лампочек за 100 лет.
Так как σk = 1/sqrt(k)/λk, и равна 0.5, то вычислим порядок потока Эрланга: k = 1/σ2/λk2 = 1/0.52/0.672 ≈ 9.
Вычислим интенсивность порождающего потока Пуассона λ = λk · k = 0.67 · 9 = 6.
19. Марковские случайные процессы.
Очень удобно описывать появление случайных событий в виде вероятностей переходов из одного состояния системы в другое, так как при этом считается, что, перейдя в одно из состояний, система не должна далее учитывать обстоятельства того, как она попала в это состояние.
Случайный процесс называется марковским процессом (или процессом без последействия), если для каждого момента времени t вероятность любого состояния системы в будущем зависит только от ее состояния в настоящем и не зависит от того, как система пришла в это состояние.
Итак, марковский процесс удобно задавать графом переходов из состояния в состояние. Мы рассмотрим два варианта описания марковских процессов — с дискретным и непрерывным временем.
В первом случае переход из одного состояния в другое происходит в заранее известные моменты времени — такты (1, 2, 3, 4, …). Переход осуществляется на каждом такте, то есть исследователя интересует только последовательность состояний, которую проходит случайный процесс в своем развитии, и не интересует, когда конкретно происходил каждый из переходов.
Во втором случае исследователя интересует и цепочка меняющих друг друга состояний, и моменты времени, в которые происходили такие переходы.
И еще. Если вероятность перехода не зависит от времени, то марковскую цепь называют однородной.
Каждый переход характеризуется вероятностью перехода Pij. Вероятность Pij показывает, как часто после попадания в i-е состояние осуществляется затем переход в j-е состояние. Конечно, такие переходы происходят случайно, но если измерить частоту переходов за достаточно большое время, то окажется, что эта частота будет совпадать с заданной вероятностью перехода.
Ясно, что у каждого состояния сумма вероятностей всех переходов (исходящих стрелок) из него в другие состояния должна быть всегда равна 1
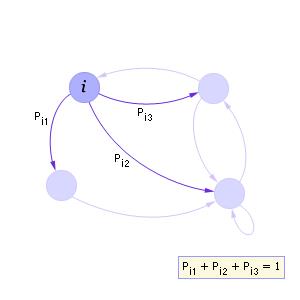
Реализация марковского процесса (процесс его моделирования) представляет собой вычисление последовательности (цепи) переходов из состояния в состояние Цепь на рис. 33.4 является случайной последовательностью и может иметь также и другие варианты реализации.
Чтобы определить, в какое новое состояние перейдет процесс из текущего i-го состояния, достаточно разбить интервал [0; 1] на подынтервалы величиной Pi1, Pi2, Pi3, … (Pi1 + Pi2 + Pi3 + … = 1), см. рис. 33.5. Далее с помощью ГСЧ надо получить очередное равномерно распределенное в интервале [0; 1] случайное число rрр и определить, в какой из интервалов оно попадает
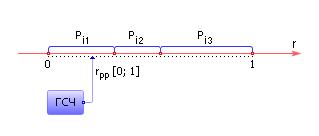
После этого осуществляется переход в состояние, определенное ГСЧ, и повтор описанной процедуры для нового состояния. Результатом работы модели является марковская цепь
20. Системы массового обслуживания: состав, типы, показатели работы, параметры.
Большой класс систем, которые сложно изучить аналитическими способами, но которые хорошо изучаются методами статистического моделирования, сводится к системам массового обслуживания (СМО).
В СМО подразумевается, что есть типовые пути (каналы обслуживания), через которые в процессе обработки проходят заявки. Принято говорить, что заявки обслуживаются каналами.
Заявки могут приходить неравномерно, каналы могут обслуживать разные заявки за разное время и так далее, количество заявок всегда весьма велико. Все это делает такие системы сложными для изучения и управления, и проследить все причинно-следственные связи в них не представляется возможным. Поэтому принято представление о том, что обслуживание в сложных системах носит случайный характер.
Примерами СМО (см. табл. 30.1) могут служить: автобусный маршрут и перевозка пассажиров; производственный конвейер по обработке деталей; влетающая на чужую территорию эскадрилья самолетов, которая «обслуживается» зенитками ПВО; ствол и рожок автомата, которые «обслуживают» патроны; электрические заряды, перемещающиеся в некотором устройстве и т. д.
Каналы — то, что обслуживает; бывают горячие (начинают обслуживать заявку в момент ее поступления в канал) и холодные (каналу для начала обслуживания требуется время на подготовку). Источники заявок — порождают заявки в случайные моменты времени, согласно заданному пользователем статистическому закону.
Очереди характеризуются правилами стояния в очереди (дисциплиной обслуживания), количеством мест в очереди (сколько клиентов максимум может находиться в очереди), структурой очереди (связь между местами в очереди). Бывают ограниченные и неограниченные очереди. Перечислим важнейшие дисциплины обслуживания. FIFO (First In, First Out — первым пришел, первым ушел): если заявка первой пришла в очередь, то она первой уйдет на обслуживание. LIFO (Last In, First Out — последним пришел, первым ушел): если заявка последней пришла в очередь, то она первой уйдет на обслуживание (пример — патроны в рожке автомата). SF (Short Forward — короткие вперед): в первую очередь обслуживаются те заявки из очереди, которые имеют меньшее время обслуживания.
Судить о результатах работы СМО можно по показателям. Наиболее популярные из них:
вероятность обслуживания клиента системой;
пропускная способность системы;
вероятность отказа клиенту в обслуживании;
вероятность занятости каждого из канала и всех вместе;
среднее время занятости каждого канала;
вероятность занятости всех каналов;
среднее количество занятых каналов;
вероятность простоя каждого канала;
вероятность простоя всей системы;
среднее количество заявок, стоящих в очереди;
среднее время ожидания заявки в очереди;
среднее время обслуживания заявки;
среднее время нахождения заявки в системе.
Судить о качестве полученной системы нужно по совокупности значений показателей.
Параметрами СМО могут быть: интенсивность потока заявок, интенсивность потока обслуживания, среднее время, в течение которого заявка готова ожидать обслуживания в очереди, количество каналов обслуживания, дисциплина обслуживания и так далее. Параметры — это то, что влияет на показатели системы.