Тема: Равносильность преобразования уравнений.
Уважаемый обучающийся, все работы выполняются в рабочих тетрадях по математике. Работа выполняется синей пастой.
Тема: Равносильность преобразования уравнений.
Цель: повторить основные понятия темы; проанализировать процесс решения уравнений и обосновать цепочку переходов от исходного уравнения к равносильному.
1. Запишите определения.
Определение. Два уравнения с одной переменной f(х) = g(х) и h(х) = р(х) называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней.
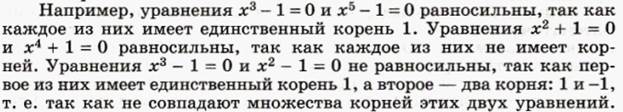
Определение. Если каждый корень уравнения f(х) = g(х) (1) является в то же время корнем уравнения h(х) = р(х) (2), то уравнение (2) называется следствием уравнения (1).
Определение. Замена одного уравнения другим равносильным ему уравнением называют равносильным преобразованием уравнения.
Если при решении уравнения совершено равносильное преобразование уравнения, то множество корней преобразованного уравнения совпадает с множеством корней исходного уравнения.
Преобразования, приводящие к равносильному уравнению: (запишите)
1. Перенос членов уравнения из одной части в другую с противоположными знаками.
2. Умножение или деление обеих частей уравнения на одно и то же число, отличное от нуля, или на выражение, имеющее постоянный знак при всех значениях неизвестного.
3. Замена части уравнения тождественно равным ему выражением.
4. Возведение уравнения в нечетную степень.
5. Извлечения корня нечётной степени из обеих частей уравнения.
6. Логарифмирование показательного уравнения.
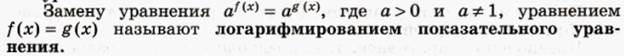
2. Рассмотрим решение примеров (записывать не нужно)

При решении уравнений часто  приходится применять несколько равносильных преобразований.
приходится применять несколько равносильных преобразований.


3. Домашнее задание (решите по образцу)
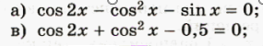 № 1.
№ 1.
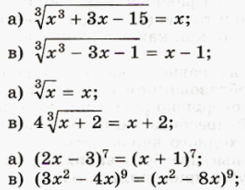 № 2.
№ 2.
№ 3.
№ 4.
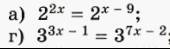 № 5.
№ 5.








