4.Каким из способов лучше решить систему?
10.02.22.г. Алгебра 9 класс.
Урок №42
Тема: Решение задач при помощи систем уравнений второй степени.
Цели и задачи: Рассмотреть различные способы решения текстовых задач практического содержания.
Не летите передо мной – я могу и не последовать,
Не летите позади меня – я могу Вас не повести,
А летите рядом со мной, ощутите радость полёта.
И будьте моими друзьями.
Ещё Платон говорил: «Человек, способный к математике, изощрён во всех науках».
Как вы понимаете это высказывание?
Таким образом, мы сегодня будем размышлять, искать простые и красивые решения, развивать логическое мышление, правильно и последовательно рассуждать, тренировать память, внимание.
Устная работа.1.Выразите одну переменную через другую
у-2х=2 х-3у+1=0 ху=6 3х+2у=5
2.Какую фигуру задаёт уравнение ?
у=0,5х²+1 х²+у²=4 ху+1=0 ху+1=0 2х+3у=4 (х-2)²+(у+3)²=49
3.Перечислите способы решения систем уравнений
4.Каким из способов лучше решить систему?
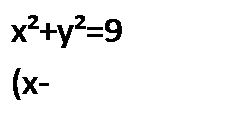
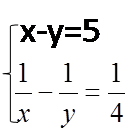
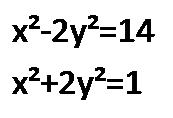
Применение систем уравнений при решении геометрических задач
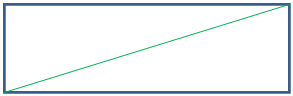
1.Диагональ прямоугольника 10 см., а одна из сторон на 2 см.больше другой. Найдите стороны прямоугольника.
 Х
Х
У
Пусть 1 сторона –х
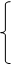 2 сторона –у
2 сторона –у
Составим систему уравнений: У-Х =2
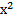 +
+ 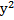 =
= 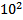
Ребята, решите эту систему.
Применение систем уравнений при решении задач на «движение» №472
2. Из двух посёлков, расстояние между которыми 40 км одновременно,
навстречу друг другу вышли два пешехода. Через 4 часа им оставалось пройти до встречи 4 километра. Если бы первый пешеход вышел на 1 час раньше, то встреча произошла бы на середине пути. С какой скоростью шёл каждый пешеход?
Р е ш е н и е
1) В задаче описано движение двух пешеходов навстречу друг другу. Известно расстояние между пунктами и расстояние, которое прошли пешеходы за 4 часа.
2) Выделим два процесса:
– реальное движение пешеходов;
– движение при условии выхода одного из пешеходов на 1 ч раньше.
3) Пусть х км/ч – скорость первого пешехода и у км/ч – скорость второго пешехода.
Заполним две таблицы:
| Реальное движение пешеходов |
| Движение с заданным условием | ||||||
| S | V | t | S | V | t | |||
| 1-й | 4х км | х км/ч | 4 ч | 1-й | 20 км | х км/ч | 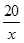 ч ч
| |
| 2-й | 4у км | у км/ч | 4 ч | 2-й | 20 км | у км/ч | 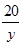 ч ч
| |
4) Известно, что расстояние от А до В равно 40 км, поэтому получим уравнение: 4х + 4у = 36. Известно, что при движении с заданным условием первый пешеход был в пути на 1 ч дольше, то есть получим уравнение: 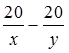 = 1. Составим систему уравнений:
= 1. Составим систему уравнений:
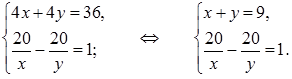 5) Решим ее способом подстановки:
5) Решим ее способом подстановки: 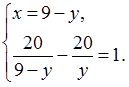
20у – 20 (9 – у) – у (9 – у) = 0; 20у – 180 + 20у – 9у + у2 = 0; у2 + 31у – 180 = 0; у1 = 5 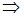 х1 = 9 – 5 = 4;
х1 = 9 – 5 = 4;
у2 = – 36 (не подходит по смыслу задачи).
6) Получаем скорости пешеходов: 4 км/ч и 5 км/ч. О т в е т: 4 и 5 км/ч.
3. Применение систем уравнений при решении задач на « смеси и сплавы»
Имеется два сплава . I сплав содержит 10% никеля, а II – 30% никеля. Из этих сплавов получили третий сплав массой 20 кг., содержащий 25% никеля. На сколько килограммов масса I сплава меньше массы II сплава?
| m сплава | % содержание никеля | m никеля в сплаве | |
| I сплав | Х | 10% | 0,1Х |
| IIсплав | У | 30% | 0,3У |
| IIIсплав | 20кг | 25% | 20*0.25 |
Составьте систему по таблице и решите задачу.
Запишите число и тему урока в тетрадь.
Разберите решение 3 задач и запишите их в тетрадь .
Прочитайте п.20 и выполните задание по ссылке: https://edu.skysmart.ru/student/vusoxufalu








