Тема. Системы логарифмических уравнений и неравенств
Дата 04.02.2022 г.
Предмет. Алгебра и начала математического анализа
Класс. 10- Б класс
Учитель. Данилова А.Ф.
Тема. Системы логарифмических уравнений и неравенств
ЗАПИШИТЕ в ТЕТРАДЬ
Четвертое февраля
Классная работа
Тема. Системы логарифмических уравнений и неравенств
Вспомним!!! При решении логарифмических уравнений и неравенств
нужно учитывать еще и следующие условия:
- Подлогарифмическое выражение может быть только положительным.
- Основание логарифма может быть только положительным и не равным единице.
№1.Запишите решение в тетрадь
Решить систему уравнений: 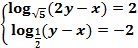 .
.
Как видим, оба уравнения являются простейшими, поэтому используем определение логарифма и получаем систему линейных уравнений:
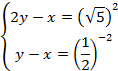
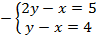
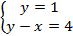
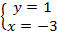
Проверка: 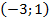 – подходит.
– подходит.
Ответ: 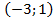 .
.
№2.Решить систему уравнений: 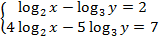 .
.
Как видим, переменная 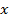 в системе встречается только в выражении
в системе встречается только в выражении 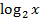 , а переменная
, а переменная 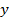 только в выражении
только в выражении 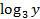 , поэтому с помощью замены:
, поэтому с помощью замены: 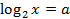 ,
, 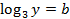 данная система сводится к системе линейных уравнений:
данная система сводится к системе линейных уравнений:
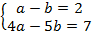
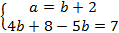
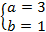
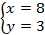
Проверка:
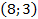 – подходит.
– подходит.
Ответ: 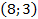 .
.
Обратите внимание в системе уравнений можно не находить ОДЗ, а выполнять проверку
Принцип решения любой системы неравенств, в том числе и логарифмических: решить каждое из неравенств по отдельности, а затем найти пересечение полученных множеств решений.
Рассмотрим конкретный пример.
№3. Решите систему неравенств 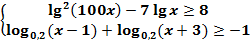 .
.
Выпишем общее ОДЗ для всей системы (объединим ОДЗ обоих неравенств):
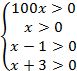
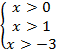
ОДЗ: 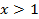 .
.
Каждое из таких неравенств мы уже умеем решать.
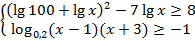
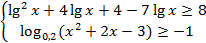
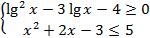
1) 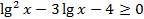
Замена: 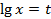 .
.
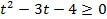

|
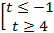
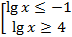
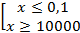
2) 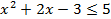
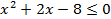

|
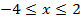
Получаем пересечение решений: 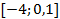 . С учётом ОДЗ получаем, что решений нет.
. С учётом ОДЗ получаем, что решений нет.
Ответ: решений нет.
Для решения подобных неравенств необходимо следующее.
Знать
Определение и свойства логарифмов.
Уметь
1) Решать логарифмические неравенства.
2) Находить пересечение множеств решений неравенств.
Домашнее задание.
1. Просмотреть видео по ссылке: https://youtu.be/DUH5tLdqd9c
2. Разобрать т записать решение неравенства 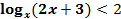 .
.
Здесь в ОДЗ необходимо также учесть, что основание логарифма должно быть больше 0 и не равно 1: 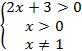 .
.
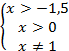
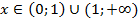
Это неравенство похоже на простейшее. С той лишь разницей, что в основании логарифма находится переменная. Поэтому при потенцировании возникают два случая: когда основание больше 1 и когда основание меньше 1.
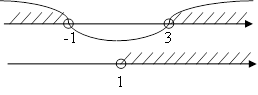
1) 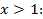
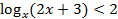
Так как 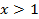 :
:
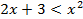
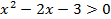
|
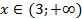
2) 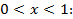
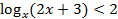
Так как 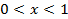 :
:
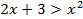
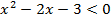
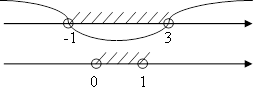
|
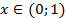
Ответ: 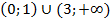 .
.
Для решения подобных неравенств необходимо следующее.
Знать
Определение и свойства логарифмов.
Уметь
Решать простейшие логарифмические неравенства.








