Тема урока: Решение систем уравнений второй степени.
09.02. 22.г. Алгебра 9 класс
Урок №41
Тема урока: Решение систем уравнений второй степени.
Цели урока:
- систематизировать знания по данной теме
- выработать умение решать системы уравнений, содержащие уравнения второй степени способами подстановки.
Математике должны учить в школе
еще с той целью,
чтобы познания, здесь приобретаемые,
были достаточными для обыкновенных
потребностей в жизни.
И.Л. Лобачевский
1. Повторим.
- Определение системы уравнения с двумя переменными.
(Уравнения, объединенные фигурной скобкой, имеющие множество решений одновременно удовлетворяющих для каждого уравнения)
- Что называют решением системы уравнений с двумя переменными?
(Пара значений, которые обращают каждое уравнение в системе в верное равенство)
- Какие уравнения называются равносильными?
(Уравнения, которые имеют одно и тоже множество решений )
- Назовите основные способы решения систем уравнений.
- Графический, метод подстановки, метод алгебраического сложения, метод замены переменной.
2. Какая фигура является графиком уравнения?
1) 3х-у=7; прямая линия
2) ху=4; гипербола
3) у-х2+2х=0;парабола
4)(х-2)2+у2=25. окружность
4.Какая из следующих пар чисел является решением системы уравнений
х 2+у2=1
у-2х=1
(0;1) (-1;-1) (1;0) (1;1)
Основными методами решения систем уравнений являются метод подстановки и метод сложения.
При этом используют приемы: замена переменных, формулы сокращенного умножения, равенство произведения нулю и другие.
3 метода решения систем уравнений.
1. Графический метод
2. Метод подстановки
3.Метод алгебраического сложения
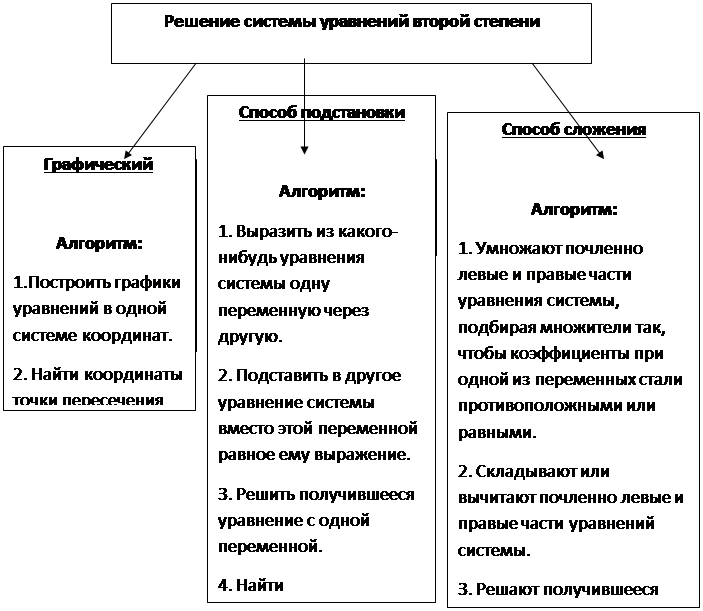
С системами уравнений мы познакомились в курсе алгебры 7-го класса, но это были системы специального вида – системы двух линейных уравнений с двумя переменными. Алгоритм, который был выработан в 7 классе, вполне пригоден для решения систем любых двух уравнений с двумя переменными х и у.
- Выразить одну переменную через другую из одного уравнения системы.
- Подставить полученное выражение вместо переменной в другое уравнение системы.
- Решить полученное уравнение относительно одной переменной.
- Подставить поочередно каждый из найденных на 3 шаге корней уравнения в выражение, полученное на первом шаге и найти другую переменную.
- Записать ответ в виде пар значений (х;у). Покажу, как работает этот метод при решении систем. Решим систему уравнений:
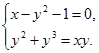
Применим метод подстановки. Преобразуем исходную систему:
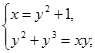
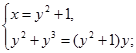
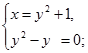
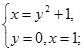
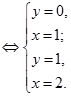Ответ: (1;0), (2;1)
Тест
Вариант 1
1. Какая из перечисленных пар является решением системы уравнений
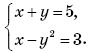А. (1; 4). Б. (4; 1). В. (–1; 4). Г. (–4; 1).
2. Из каких уравнений можно составить систему уравнений, решением которой будет пара чисел (1; 0)? А. xy = 4. Б. 5x + y = 8. В. 4x + y = 4. Г. x2 + y2 = 1.
3. Сколько решений имеет система уравнений
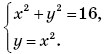А. Одно. Б. Два. В. Три. Г. Четыре.
4. Решение какой системы уравнений изображено на рисунке?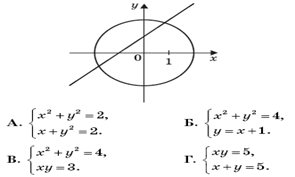 
5. Решите систему уравнений
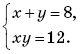
А. (2;6). Б.(6;2). В.(2;6)и(6;2). Г. (–2; –6) и (–6; –2).
Вариант 2
1. Какая из перечисленных пар является решением системы уравнений
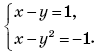
А. (3;2). Б.(2;3). В.(–3;2). Г. (–2; 3).
2. Из каких уравнений можно составить систему уравнений, решением которой будет пара чисел (0;1)?
А. 5x–4y=3. Б.7x+2y=2. В.x2 +y2 =1. Г. xy = 7.
3. Сколько решений имеет система уравнений
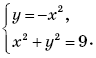
А. Одно. Б.Два. В.Три. Г. Четыре.
4. Решение какой системы уравнений изображено на рисунке?
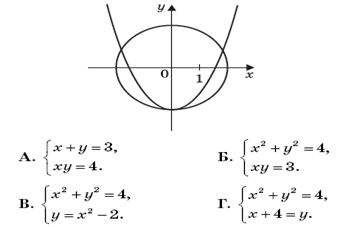
5. Решите систему уравнений
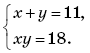
А. (2;9). Б.(9;2). В.(9;2)и(2;9). Г. (–9; –2) и (–2; –9)
Проверили свой тест и поставьте себе оценку
5 правильных ответов «5»
4 правильных ответов «4»
3 правильных ответа «3»
2 правильных ответа «2»
ОТВЕТЫ К ТЕСТ
| № | Вариант 1 | Вариант 2 |
| 1 | Б | А |
| 2 | В,Г | Б,В |
| 3 | Б | Б |
| 4 | Б | В |
| 5 | В | В |
Ребята, прочитайте п. 19 учебника и посмотрите видео урок по ссылке:
Решение систем уравнений второй степени. 9 класс.
YouTube
Проработайте урок№41.
Запишите число и тему урока в тетрадь..
Запишите алгоритм решения систем уравнений второй степени.
Решите систему и выполните тест
Домашнее задание: По учебнику п.19, выполните
№ 429(в), №434(а), №437(б).