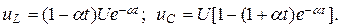Переходные процессы в неразветвленных электрических цепях
Лабораторная работа 14 ( Lr 14)
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В НЕРАЗВЕТВЛЕННЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
ЦЕЛЬ РАБОТЫ
Экспериментальное исследование апериодических и колебательных переходных процессов в линейных электрических цепях первого и второго порядков и сопоставление экспериментальных результатов с предварительно рассчитанными параметрами.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ И РАСЧЁТНЫЕ ФОРМУЛЫ
1. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЦЕПЯХ
Переходным процессом называют процесс изменения токов и напряжений в цепи при переходе от одного установившегося режима к другому. Причиной, вызывающей начало переходного процесса, является коммутация, под которой понимают отключение цепи или её подключение к внешнему источнику питания, либо скачкообразное изменение топологии или параметров элементов цепи. В общем случае вид кривой переходного процесса зависит как от изменения топологии цепи, накопленной в ней энергии, так и от видов действующих в цепи ЭДС источников напряжения и токов источников тока.
Переходный процесс в цепи может протекать как за счёт начального запаса энергии, накопленного в реактивных L и C элементах, так и за счёт энергии внешнего источника. При этом переходный процесс, протекающий за счёт расходования накопленной в элементах L и С энергии, называют свободным процессом или процессом собственных колебаний, а режим, близкий к стационарному, который устанавливается в цепи по истечении времени переходного процесса с момента коммутации, называют установившимся режимом; напряжения и токи в установившемся режиме называют установившимися напряжениями и токами.
В общем случае напряжения и токи цепи в переходном режиме выражают в виде суммы установившихся и свободных составляющих, т. е.
u =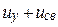 
и i = 
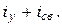
2. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЦЕПЯХ
ПЕРВОГО ПОРЯДКА
На рис. 14.1 и рис. 14.2 изображены схемы RL - и RC-цепей, входы которых подключаются к источникам постоянного напряжения U. В линейных цепях первого порядка переходные процессы описываются экспоненциальными уравнениями.
Для RL-цепи (рис. 14.1, а) ток и напряжение на индуктивной катушке:
i L(t) = I0(1- e -at) = I0(1- e -t/ t ); u L(t) = L[di L(t)/dt] = Ue - at,
где I0 = U / R - установившийся ток; t = L/R - постоянная времени в секундах; а = 1/t - коэффициент затухания переходного процесса (1/c).
 |
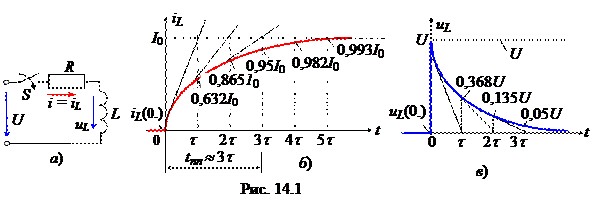Графики тока i L(t) и напряжения u L(t) представлены на рис. 14.1, б и в, где t = 0- означает мгновение до коммутации.
Анализ графиков показывает, что ток в RL -цепи постепенно нарастает до своего установившегося значения и тем медленней, чем бóльше постоянная времени t - время, в течение которого переходная величина (ток в нашем случае) изменяется на 0,632 от своего размаха I0.
Если снять осциллограмму переходного тока, то значение t можно определить по длине подкасательной, получаемой после проведения касательной из точки 0 до пересечения с горизонтальной линией (I0) и опускания перпендикуляра на ось абсцисс (или используя другие точки осциллограммы для проведения касательной, например, точку 0,632I0 или точку 0,865I0 (см. рис. 14.1, б)).
В инженерных расчётах время переходного процесса принимают равным t пп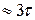 
; при этом переходная величина достигает порядка 0,95 своего установившегося значения. При более точных расчётах принимают t пп 
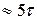, при котором переходная величина, в нашем случае ток, i L(5t) » 0,993I0.
На графике u L(t) (рис. 14.1, в) длина подкасательной на оси абсцисс соответствует постоянной времени t цепи, в течение которого значение напряжения u L(0+) = U уменьшается в e » 2,72 раз. Чем больше t, тем медленнее уменьшается напряжение u L.
 |
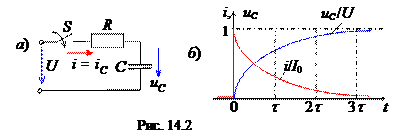При подключении RC-цепи (рис. 14.2, а) к источнику постоянного напряжения U напряжение и ток конденсатора равны:
u С(t) = U(1- e - t/t ); i С(t) = С[du C(t)/dt] = I0e - at = I0e - t/t,
где I0 = U / R - ток при t = 0+; t = R С - постоянная времени; а = 1/t - коэффициент затухания переходного процесса; t = 0+ – мгновение после коммутации.
Нормированные графики u C(t)/U и i C(t)/U представлены на рис. 14.2, б.
Если сравнить графики переходного тока i L и напряжения u L в RL-цепи (рис. 14.1, б) с током i C и напряжением u C в RC-цепи (рис. 14.2, б), то можно заметить, что графики i L и u C, u L и i C внешне идентичны, так как законы изменения переходных величин одинаковые.
3. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНОЙ ЦЕПИ
ВТОРОГО ПОРЯДКА
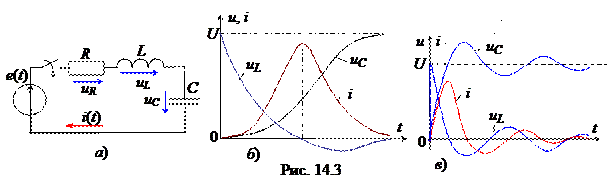
В цепи второго порядка характер изменения тока и напряжений на индуктивной катушке и конденсаторе зависит от соотношения параметров элементов R, L и С последовательной RLC-цепи (рис. 14.3, а):
а) при R > 2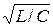 
(при неравных вещественных отрицательных корнях -а1 и -а2 характеристического уравнения 
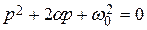цепи, где a = R /2L; 
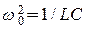) переходный процесс носит апериодический характер (рис. 14.3, б):
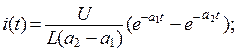
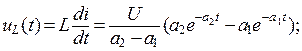
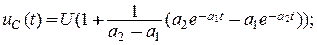
б) при R < 2 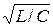(при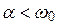 
корни характеристического уравнения 
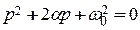комплексно-сопряжены: 
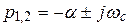, где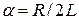 
- коэффициент затухания переходного процесса;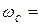 
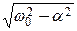- угловая частота свободных (собственных) колебаний реального контура; 
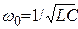- собственная частота идеального контура (при R = 0)) переходный ток
.
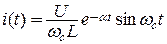Определив постоянную времени цепи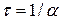 
и период собственных колебаний тока Т св = 2p / 
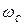, строим график тока i(t) (рис. 14.4).
 |
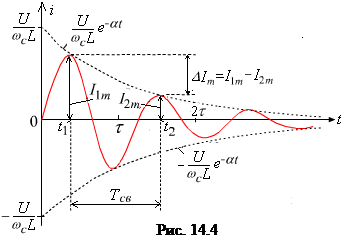Из полученного аналитического выражения тока, а также из графика видно, что переходный процесс в этом случае является колебательным вследствие периодического перераспределения запасов энергии в магнитном и электрическом полях элементов L и С цепи.
Скорость затухания колебаний тока в переходном процессе зависит от постоянной времени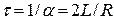 
цепи и определяется декрементом затухания 
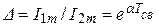или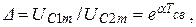 
а логарифм натуральный от D называют логарифмическим декрементом затухания
.
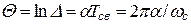Откуда коэффициент затухания
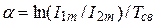или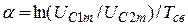 
.
Как видно из выражения декремента Q, за период Т св ток i затухает в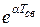 
раз.
Графики напряжений (пр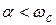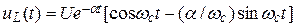и 
) 
и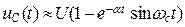 
и тока i(t) изображены на рис. 14.3, в. Напряжения и ток периодически меняют знак. Амплитуда колебаний изменяется по экспоненциальному закону; следовательно, в цепи совершаются затухающие колебания тока и напряжений с периодом Т св = 2p / .
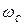В предельном случае a = 0 (R = 0),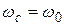 
колебания будут незатухающими с периодом Т0 = 2p 
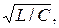соответствующими характеру этих кривых при установившемся процессе в случае резонанса напряжений;
в) в другом предельном случае, когда сопротивление, называемое критическим, равно R кр = 2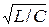 
( 
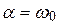и корни p1 = p2 = - a = - R /2L уравнения 
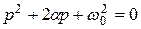вещественны и равны друг другу), получим 
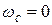и Т св = ¥. При этом периодические затухающие колебания переходят в апериодические. Этот случай называют критическим (предельно апериодическим), а ток i, напряжения на катушке u L и на конденсаторе u C в переходном процессе определяют по формулам:
i = (U / L) te - a t; 