Тема: Определители.
Практическое занятие.
Тема: Определители.
Квадратной матрицей порядка 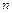 называется квадратная таблица из чисел
называется квадратная таблица из чисел 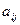 (
( 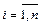 ,
, 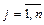 ):
): 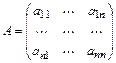 , состоящая из
, состоящая из 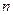 строк и
строк и 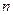 столбцов. Любой квадратной матрице
столбцов. Любой квадратной матрице 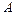 порядка
порядка 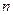 можно поставить в соответствие число
можно поставить в соответствие число 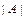 , равное алгебраической сумме
, равное алгебраической сумме 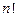 слагаемых, составленных определённым образом из элементов
слагаемых, составленных определённым образом из элементов 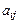 матрицы
матрицы 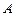 , называемое определителем матрицы.
, называемое определителем матрицы.
Определителем 1-ого порядка называется число 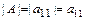 .
.
Определителем 2-ого порядка называется число 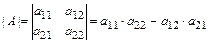 .
.
Определителем 3-его порядка называется число
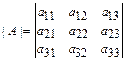
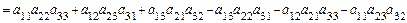
Минором элемента 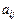 определителя
определителя 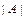 называется определитель
называется определитель 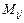 , полученный из данного вычёркиванием
, полученный из данного вычёркиванием 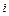 -ой и
-ой и 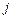 -ого столбца. Алгебраическим дополнением
-ого столбца. Алгебраическим дополнением 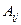 элемента
элемента 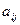 называется его минор
называется его минор 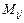 , взятый со знаком
, взятый со знаком 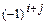 :
: 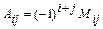 .
.
Определителем порядка 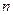 называется число
называется число
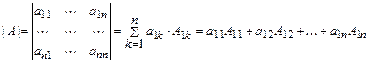
Разложением определителя 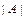 по
по 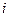 -ой строке (
-ой строке ( 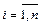 ) называется соотношение:
) называется соотношение:
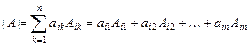 .
.
Разложением определителя 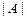 по
по 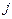 -ому столбцу (
-ому столбцу ( 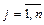 ) называется соотношение:
) называется соотношение:
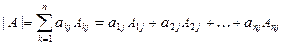
Определители обладают свойствами:
1) определитель не изменится при замене всех его строк столбцами с теми же номерами;
2) определитель изменит знак на противоположный, если переставить местами любые две строки (два столбца) определителя;
3) общий множитель элементов какой-либо строки (столбца) можно вынести за знак определителя;
4) определитель равен нулю, если он содержит нулевую строку (столбец), две одинаковые или пропорциональные строки (столбца);
5) определитель не изменится, если к какой-либо строке (столбцу) прибавить другую строку (столбец), умноженную на любое число;
6) определитель треугольного вида (когда все элементы, лежащие по одну сторону одной из его диагоналей равны нулю) равен произведению диагональных элементов.
В задачах 1.1-1.4 вычислить определители 2-го порядка.
1.1 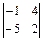 . 1.2
. 1.2 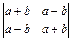 . 1.3
. 1.3 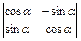 . 1.4
. 1.4 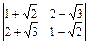 .
.
В задачах 1.5-1.8 вычислить определители 3-го порядка.
1.5 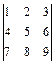 . 1.6
. 1.6 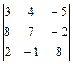 . 1.7
. 1.7 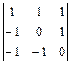 . 1.8
. 1.8 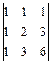 .
.
1.9 Решить уравнение. а) 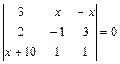 ; б)
; б) 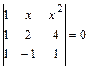 ; в)
; в) 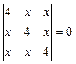 .
.
1.10 Решить неравенство.  а)
а) 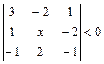 ; б)
; б) 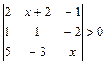 ; в)
; в) 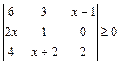 .
.
В задачах 1.11-1.16, используя свойства определителя, доказать тождества (определители не развертывать).
1.11 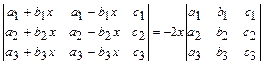 . 1.12
. 1.12 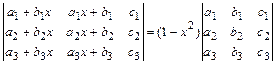 .
.
1.13 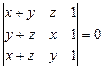 . 1.14
. 1.14 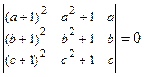 .
.
1.15 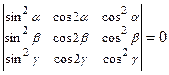 . 1.16
. 1.16 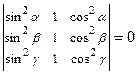 .
.
В задачах 1.18-1.23 вычислить определители, используя разложение по строке или столбцу:
1.18 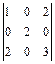 . 1.19
. 1.19 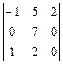 . 1.20
. 1.20 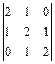 . 1.21
. 1.21 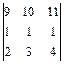 . 1.22
. 1.22 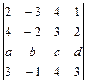 . 1.23
. 1.23 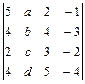 .
.
В задачах 1.24-1.29 вычислить определители
1.24 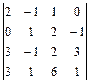 . 1.25
. 1.25 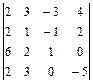 . 1.26
. 1.26 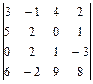 .
.
1.27 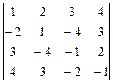 . 1.28
. 1.28 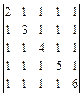 . 1.29
. 1.29 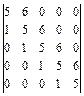 .
.
Ответы:
1.1 18 1.2 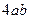 1.3 1 1.4
1.3 1 1.4 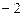 1.5 0 1.6 0 1.7 1 1.8 1 1.9
1.5 0 1.6 0 1.7 1 1.8 1 1.9 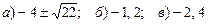
1.10 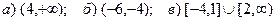 1.18
1.18 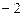 1.19
1.19 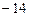 1.20 4 1.21 0
1.20 4 1.21 0
1.22 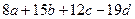 1.23
1.23 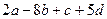 1.24 0 1.25 48 1.26 223 1.27 900 1.28 394 1.29 665
1.24 0 1.25 48 1.26 223 1.27 900 1.28 394 1.29 665








