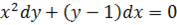2. Гіпербола її канонічне рівняння

Дата: 2025-06-02; Просмотры: 10

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

3. Таблиця основних невизначених інтегралів.

4. Поняття функції багатьох змінних.

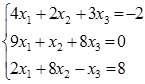5. Розв'язати систему лінійних алгебраїчних рівнянь за допомогою оберненої матриці.

6. Дано вершини трикутника АВС А(-5;-3), В(7;6), С(5;-8). Знайти:

· довжину сторони АВ;

· рівняння сторін АВ і АС та їхні кутові коефіцієнти;

· внутрішній кут А в радіанах з точність до 0,01;

· рівняння висоти СD і її довжину;

· рівняння кола, для якого висота СD є діаметром;

· систему лінійних нерівностей, які визначають трикутник АВС.

7. Обчислити інтеграл.

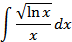
8. Обчислити площу фігури, обмежену лініями , .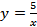

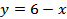9. Задано функцію 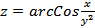, точку 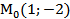і вектор .

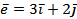Знайти: а) 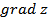в точці 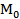; б) похідну в точці 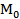в напрямку вектора .

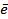10. Зінтегрувати диференціальне рівняння: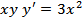

11. Знайти інтервал збіжності степеневого ряду

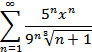
Затверджено на засіданні кафедри вищої математики та інформатики

Протокол № 4 від 24 листопада 2011 року.

Завідувач кафедри д.т.н., професор І.П. Васильченко

Екзаменатор д.т.н., професор І.П. Васильченко

МІНІСТЕРСТВО ФІНАНСІВ УКРАЇНИ

УКРАЇНСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ ФІНАНСІВ ТА МІЖНАРОДНОЇ ТОРГІВЛІ

2011-2012 навчальний рік

Спеціальність „Облік і аудиит”,

Курс 1 освітньо-кваліфікаційний рівень бакалавр

Навчальний предмет „Вища математика”

ЕКЗАМЕНАЦІЙНИЙ БІЛЕТ № 4

1. Векторно-матричний спосіб розв'язку систем.

2. Друга визначна границя. Число “е”.

3. Метод заміни змінної у невизначеному інтегралі.

4. Означення диференціали. Функції багатьох змінних.

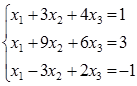5. Розв'язати систему лінійних алгебраїчних рівнянь за правилом Крамера.

6. Дано вершини трикутника АВС А(-6;-2), В(6;7), С(4;-7). Знайти:

· довжину сторони АВ;

· рівняння сторін АВ і АС та їхні кутові коефіцієнти;

· внутрішній кут А в радіанах з точність до 0,01;

· рівняння висоти СD і її довжину;

· рівняння кола, для якого висота СD є діаметром;

· систему лінійних нерівностей, які визначають трикутник АВС.

7. Обчислити інтеграл.

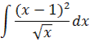
8. Обчислити площу фігури, обмежену лініями , .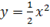

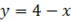9. Задано функцію 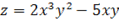, точку 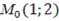і вектор .

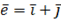Знайти: а) 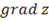в точці 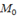; б) похідну в точці 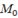в напрямку вектора .

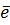10. Зінтегрувати диференціальне рівняння: