Глава 3. Количественная оценка результатов исследование и установление связи между результатом и фактором

Дата: 2025-06-02; Просмотры: 22
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

 

Статистические данные по бомбардирам ТОП-5 чемпионатов Европы по футболу и Российской Премьер лиги за сезон 2019-2020 представлены в таблице

Имя Фамилия Клуб Кол-во голов

Российская Премьер лига
Сердар Азмун Зенит 17
Артём Дзюба Зенит 17
Евгений Луценко Арсенал 15

Английская Премьер лига
Джейми Варди Лестер 23
Дэнни Ингс Саутгемптон 22
Пьер-Эмерик Обамеянг Арсенал 22

Немецкая Бундеслига
Роберт Левандовски Мюнхенская Бавария 34
Тимо Вернер РБ Лейпциг 28
Джейдон Санчо Дортмундская Боруссия 17
Имя Фамилия Клуб Кол-во голов
Килиан Мбаппе Пари Сен-Жермен 18
Виссам Бен-Йеддер Монако 18
Мусса Дембеле Лион 16

Испанская Примера
Лионель Месси Барселона 25
Карим Бензема Реал Мадрид 21
Жерар Морено Вильярреал 18

Итальянская Серия А
Чиро Иммобиле Лацио 36
Криштиану Роналду Ювентус 31
Ромелу Лукаку Миланский Интер 23

 

1. Составим вариационный ряд: 15, 16, 17, 17, 17, 18, 18, 18, 21, 22, 22, 23, 23, 25, 28, 31, 34, 36

2. Найдём моду вариационного ряда: Вариационный ряд имеет 2 моды: 17 и 18. Ряд является бимодальным.

3. Найдём медиану вариационного ряда. Вариационный ряд включает в себя чётное число единиц, поэтому медиана определяется как средняя из двух центральных значений (21+22)/2=21,5

4. Найдём размах вариации вариационного ряда. Разница между максимальным и минимальным значением вариационного ряда равна 21.

5. Составим таблицу распределения вариационного ряда:

Xi Ni
15 1
16 1
17 3
18 3
21 1
22 2
23 2
25 1
28 1
31 1
34 1
36 1
∑ 18

6. Построим полигон частот

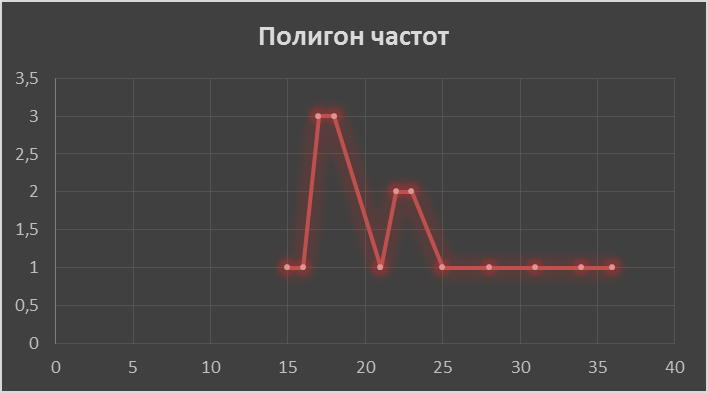
7. Найдём выборочное среднее вариационного ряда. Выборочная средняя вариационного ряда равна:

(15+16+17×3+18×3+21+22×2+23×2+25+28+31+34+36)/18 = 22,278

8. Найдём дисперсию вариационного ряда:

x |x – xср| (x – xср)2
15 7.278 52.969
16 6.278 39.526
17 5.278 27.952
17 5.278 27.952
17 5.278 27.952
18 4.278 18.378
18 4.278 18.378
18 4.278 18.378
21 1.278 1.656
22 0.278 0.082
22 0.278 0.082
23 0.722 0.521
23 0.722 0.521
25 2.722 7.409
28 5.722 32.741
31 8.722 76.073
34 11.722 137.405
36 13.722 188.293
401 88,111 676,287

D = 676,287 / 18 = 37,57

9. Найдём среднее квадратичное отклонение вариационного ряда: 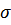= √37,57 = 6,129

10. Найдём исправленную дисперсию: 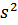= 18/17 × 37,57 = 39,78

11. Найдём исправленное среднее квадратичное отклонение вариационного ряда: s = √39,78 = 6,3

12. Корреляционный анализ:

В качестве факторного признака нами было выбрано количество игр (в таблица факторный признак обозначен под индексом x)

28 28 28 35 38 36 31 34 32 20 26 27 33 37 35 37 33 36

 

Коэффициент корреляции Пирсона

x y x – xср y – yср ( x – xср ) × ( y – yср ) (x – xср)2 (y – yср)2
28 17 3.9 5.278 20.584 15.21 27.952
28 17 3.9 5.278 20.584 15.21 27.952
28 15 3.9 7.278 28.419 15.21 52.969
35 23 3.1 0.722 2.238 9.61 0.521
38 22 6.1 0.278 1.696 37.21 0.082
36 22 4.1 0.278 1.14 16.81 0.082
31 34 0.9 11.722 10.55 0.81 137.405
34 28 2.1 5.722 12.016 4.41 32.741
32 17 0.1 5.278 0.528 0.01 27.952
20 18 11.9 4.278 50.908 141.61 18.378
26 18 5.9 4.278 25.24 34.81 18.378
27 16 4.9 6.278 30.762 24.01 39.526
33 25 1.1 2.722 2.994 1.21 7.409
37 21 5.1 1.278 6.518 26.01 1.656
35 18 3.1 4.278 13.262 9.61 18.378
37 36 5.1 13.722 69.982 26.01 188.293
33 31 1.1 8.722 9.594 1.21 76.073
36 23 4.1 0.722 2.96 16.81 0.521

сумма

 309.975 395.78 676.268

 

Rx,y = 309.975/√(676.268×395.78) = 0.60

Вывод: Между количеством голов и количеством сыгранных матчей наблюдается прямая, средняя (заметная) связь.

Проверка: Тнабл = Rx,у×√(n–2)/√(1–Rx,у2) = 0.6×√16×√(1–0.62) = 1.92

Тнабл > Ткр

Вывод: коэффициент корреляции существенный

Коэффициент корреляции Спирмена

x y dx dy ∆d (∆d)2
28 17 5 4 1 1
28 17 5 4 1 1
28 15 5 1 4 16
35 23 12.5 12.5 0 0
38 22 18 10.5 7.5 56.25
36 22 14.5 10.5 4 16
31 34 7 17 -10 100
34 28 11 15 -4 16
32 17 8 4 4 16
20 18 1 7 -6 36
26 18 2 7 -5 25
27 16 3 2 1 1
33 25 9.5 14 -4.5 20.25
37 21 16.5 9 7.5 56.25
35 18 12.5 7 5.5 30.25
37 36 16.5 18 -1.5 2.25
33 31 9.5 16 -6.5 42.25
36 23 14.5 12.5 2 4
сумма   171 171   439.5

 

Rs = 1 – (6×439.5)/(18×(182–1)) = 1 – 2637/5814 = 0.546

Вывод: Между количеством голов и количеством сыгранных матчей наблюдается прямая, средняя (умеренная) связь

Проверка: Тнабл= Rs × (√(n-2)/√(1-Rs^2)) = 0.546×(√16)/√(1-0.546^2) = 2.606

Тнабр>Ткр

Вывод: коэффициент корреляции существенный

Заключение

 

На основе проделанных исследований, мы можем сделать вывод, что количество сыгранных игр имеет среднее влияние на количество голов бомбардиров. Согласно корреляции Пирсона (0.6) связь между двумя показателями средняя (заметная). Исходя из полученных результатов можно сделать несколько выводов:

1. показатель количества игр в отношение количества голов, хоть и является важным, но всё же не остаётся единственным и главенствующим;

2. можно сделать предположение, что роль одного важного человека в команде, который делает всю игру, присутствует, но не во всех командах является важной причиной высокого положения команды в турнирной таблице.

Однако для более полного результата нужно проводить более объёмные исследования, принимая во внимание не только количество игр, но и позицию игрока, количество созданных голевых моментов и тому подобное.

 

Список литературы

 

1. Афанасьев В.В. Теория вероятностей: учеб. пособие для студентов вузов. – М.: Гуманитар. Изд. Центр ВЛАДОС, 2007. – 350 с.

2. Афанасьев В.В., Сивов М.А. Математическая статистика в педагогике. – Ярославль: ЯГПУ, 2010. – 75 с.

3. Баврин И.И. Математика для гуманитариев. – М., 2011. – 320 с.

4. Гмурман В. Е. Теория вероятностей и математическая статистика : учебник для вузов / В. Е. Гмурман. – Москва : Издательство Юрайт, 2020. – 479 с.

5. Кремер Н. Ш. Математическая статистика : учебник и практикум для вузов / Н. Ш. Кремер. – Москва : Издательство Юрайт, 2020. – 259 с.

6. Математическая статистика для социологов. Задачник : учебное пособие для вузов / ответственный редактор Ю. Н. Толстова. – Москва : Издательство Юрайт, 2020. – 199 с.

7. Новиков Д.А. Статистические методы в педагогических исследованиях (типовые случаи) [Электронный ресурс]: монография/ Д.А. Новиков. – Электрон. текстовые данные. – М.: МЗ-Пресс, 2004. – 67 c. – Режим доступа: http://www.iprbookshop.ru/8501.html.

8. Статистика игроков, Бомбардиры [Электронный ресурс]. URL: https://www.championat.com/football/

9. Голдблатт Дэвид; Актон Джонии Футбол. Самая полная энциклопедия / пер. с анг. А.Е. Зуенко, В.П. Никитина, Е.В. Олейниковой, Д.В. Спирина. – М.:РОСМЭН, 2017. – 400 с.