Глава 2. Вероятностный анализ азартных игр
Как же можно посчитать свой возможный выигрыш? И можно ли это сделать вообще? Как я уже отметила в предыдущей главе – можно. Теперь попытаемся ответить на вопрос, как это сделать?
Математическое ожидание дискретной случайной величины есть сумма произведений всех её возможных значений на их вероятности:
M(X) = x1p1 + x2p2 + ... + xnpn
Применительно к игре математическое ожидание является суммой, которую вы можете заработать или проиграть в среднем по каждой ставке. На языке игроков это иногда называется преимуществом игрока (если оно положительно для игрока), или преимуществом казино (если оно отрицательно для игрока)[6].
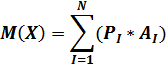
Где P – вероятность выигрыша или проигрыша
A – выигранная или проигранная сумма
N– количество возможных результатов
Предположим, вы играете в кости. При выпадении 5 и 6 очков вы выигрывайте 5 очков, а при выпадении 1, 2, 3 и 4 – проигрывайте 3 очка. Посчитаем математическое ожидание.
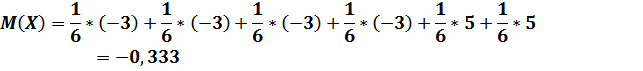
Как мы видим математическое ожидание отрицательное, что делает игру не обоснованной. Попробуем поднять выигрыш до 6 очков.
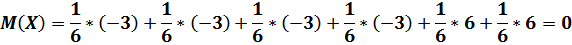
Вот на таких условиях можно играть. А теперь попробуем поднять выигрыш до 7 рублей.
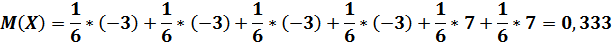
Как мы видим математическое ожидание положительное, что даёт больше шансов на выигрыш. Таким образом, можно выиграть, если изначально будет потенциал для получения приза. Для этого нужно сделать нехитрые вычисления: проверить с помощью математического ожидания непосредственно само число и, если оно окажется положительным, то стоит надеяться на выигрыш. Собственно, как показывают расчеты, выяснить это несложно. На уроках математики вполне возможно решать задачи и выяснять, сможем ли мы заработать деньги при игре в кости или нет. Как мы видим, шансы есть. Нужно лишь правильно посчитать.
Лотереи:
Ещё из советских времён пришли к нам лотереи. Гениальным режиссёром Леонидом Иовичем Гайдаем даже был снят фильм «Спортлото 82». Опустим художественные подробности фильма и попробуем посчитать, какой шанс на выигрыш дают нам лотереи. Сначала о правилах. В купленной карточке нужно зачеркнуть 5 из 36 чисел, либо 6 из 49 в зависимости от варианта игры. Одну часть билета отправить по почте, другую оставить себе. Затем при помощи лототрона и шаров определяется выигрышная комбинация. Давайте немного окунёмся в математику. Для того чтобы узнать шанс на выигрыш, воспользуемся следующей формулой (где m – количество шаров, которые необходимо угадать, играя в лотерею, а n – количество шаров в лототроне).
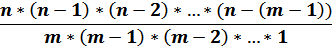
Для лотереи 6 из 49:
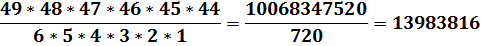
Для лотереи 5 из 36:
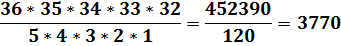
Вот оно истинное лицо числовых лотерей. Теперь понятна вся мизерность шанса на выигрыш в лотерею. Кажется, что может быть проще угадать 6 чисел из 49? А угадать одно число из 13 983 816 чисел реально? Запомните – это одно и то же.
Из почти 14 миллионов игроков в лотерею лишь одному может выпасть шанс угадать все шесть чисел. Действительно стоило создать фильм об этом великом событии. Таким образом, математически предсказать выигрышную комбинацию невозможно. Здесь большую роль играет случайность и везение. Может, это покажется и неинтересным на уроках математики, зато может заставить кого-то задуматься и отказаться от желания испытывать судьбу на деньги. Если мы купим даже 100 лотерейных билетов и будем пытаться математически подбирать возможные комбинации чисел, то мы сможем лишь ненамного приблизиться к возможному выигрышу. Это может быть полезным только лишь с точки зрения формирования навыка решения задач с применением формул теории вероятности.
Европейская рулетка (рулетка Монте – Карло):
Колесо рулетки Монте - Карло имеет 37 секторов, секторы 1, 3, 5, 7, 9 ,13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35 красные; секторы 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36 чёрные и сектор 0, он же ZERO – зелёного цвета.
Если не считать 0 , секторы на колесе рулетки чередуются между красным и чёрным. Такой странный порядок чисел на колесе предназначен для того, чтобы большие и маленькие числа, так же как чётные и нечётные числа, имели тенденцию чередоваться.
Ставки казино:
Прямая ставка или ставка на число – является ставкой на единственное число и оплачивается в случае выигрыш 35:1, т. е. при выпадении выбранного вами числа выигрыш равен 35 единицам, в других случаях вы поигрываете одну единицу (ставку).
Ставка на 2 числа является ставкой на два смежных числа в таблице на столе рулетки. Фишка ставится на черту, разделяющую два номера. Выигрыш оплачивается как 17:1, если выпадает любое из выбранных чисел.
Ставка на 3 числа (или ставка на строку C) является ставкой на три числа в вертикальной строке таблицы. Фишка ставится на вертикальную черту, ограничивающую ряд справа. Выигрыш оплачивается как 11:1, если при одном вращении колеса рулетки выпадет одно из трёх чисел.
Ставка на 4 числа (D) является ставкой на четыре числа, которые образуют квадрат на столе рулетки. Фишка ставится на угол между четырьмя номерами. Выигрыш оплачивается как 8:1, если при одном вращении колеса рулетки выпадает одно из 4 чисел.
Ставка на 6 чисел (F) является ставкой на шесть чисел в двух смежных строках. Выигрыш оплачивается как 5:1, если выпадает одно из выбранных чисел.
Ставка на 12 чисел. Ставки на 12 чисел могут быть сделаны несколькими способами. Ставка на столбец (G) делается на любой из трёх столбцов, расположенных горизонтально на столе. Фишка ставится на поле возле выбранной колонки.
Другие ставки на 12 чисел (H) – первая дюжина (1 – 12), средняя дюжина (13 – 24) и последняя дюжина (25 – 36). Ставки на 12 чисел оплачиваются как 2:1, если выпадает одно из выбранных чисел. Ставка на 12 чисел проигрывает, если выпадает 0.
Ставки на 18 чисел. Ставка на цвет (I) является ставкой на красное или чёрное.
Ставка на чёт – нечет (K) является ставкой на чётные числа от 1 до 36 или на нечётные числа от 1 до 36. Малая ставка (J) является ставкой на числа 1 – 18, и большая ставка является ставкой на числа от 19 до 36.
Ставки на 18 чисел оплачиваются 1:1, если при одном вращении колеса рулетки выпадает одно из выбранных чисел. Ставка на 18 чисел проигрывает, если выпадает 0.
Определим величину ожидаемого выигрыша при различных ставках:
X – величина выигрыша (проигрыша)
P(X) – вероятность выигрыша (проигрыша)
Ставка на число
| X | -1 | 35 |
| P(X) | 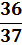
| 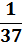
|
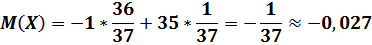
Как мы видим математическое ожидание в данном случае отрицательное, т. е. на каждую поставленную единицу ожидается проигрыш около 0,03 этой единицы.
Ставка на пару чисел
| X | -1 | 17 |
| P(X) | 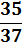
| 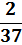
|
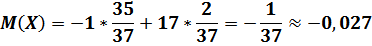
Ставка на четыре числа
| X | -1 | 8 |
| P(X) | 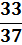
| 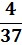
|
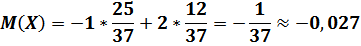
Ставка на дюжину
| X | -1 | 2 |
| P(X) | 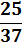
| 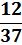
|
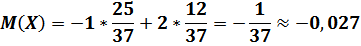
Как мы видим, правила игры созданы так, что с повышением вероятности того, что произойдёт определённое событие, уменьшается ставка на это событие, при этом математическое ожидание остаётся неизменным. Таким образом, делаем вывод о том, что европейская рулетка или, проще говоря, казино далеко не является местом, где люди выигрывают большие суммы денег, скорее даже наоборот. В самих правилах игры заложена математическая закономерность не повышающая, а понимающая вероятность выигрыша. Тем не менее, мы видим, что просчитать вероятность выигрыша возможно. Однако правила казино не позволят нам сделать его очень большим. Нужно очень долго прорешивать возможные комбинации, чтобы выиграть большую сумму денег.
Игровые автоматы:
Сейчас игровые автоматы не встретишь ни в торговых, ни в развлекательных центрах, а ведь ещё совсем недавно они стояли прямо на улицах и каждый мог испытать свою судьбу. При этом, как правило, вы либо проигрывали, либо оставались в незначительном выигрыше. Попробуем разобраться, был ли шанс разбогатеть, играя на них.
О правилах:
Стоимость одной игры составляла пять рублей. Выигрыш варьировался в зависимости от комбинации трёх цифр на игровом табло. Величина выигрыша равнялась произведению пяти рублей и количеству монет, указанному в таблице. Например, 444=50 обозначает, что при выпадении числа 444 ваш выигрыш составит 50 пятачков. Рассчитаем вероятность выпадения каждой комбинации. При расчётах будем исходить из того, что выпадение любой из цифр равновероятно.
Посчитаем вероятность выпадения трёх одинаковых цифр:
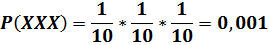
Вероятность выпадения двух одинаковых цифр в схемах Y00 и Y77 равна:
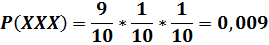
Расклад вида YY0 и YY7 означает, что второй цифрой не может стоять 0 и 7 соответственно (так как это приведёт к появлению других комбинаций), а первая цифра может быть вообще любой, отсюда:
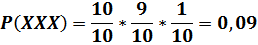
Сведём в таблицу сумму и вероятность выигрыша
| X | 5 | 10 | 25 | 50 | 75 | 75 | 100 |
| P | 0 ,09 | 0,09 | 0,009 | 0,009 | 0,001 | 0,001 | 0,001 |
| X | 100 | 125 | 125 | 250 | 250 | 500 | 1000 |
| P | 0,001 | 0,001 | 0,001 | 0,001 | 0,001 | 0,001 | 0,001 |
И посчитаем математическое ожидание выигрыша:
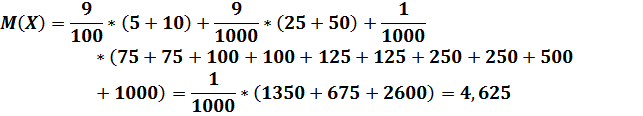
В результате мы видим, что математическое ожидание выигрыша меньше пяти рублей, хотя и ненамного, что делает игру обоснованной при однократном испытании, но при продолжительной игре результат будет уже просто удручающим. Так что заработать на такой игре вряд ли удастся.
Таким образом, мы можем сделать вывод из всего вышеописанного, что азартные игры не являются лёгким и быстрым способом заработка денег. Однако возможность просчитать выигрыш существует. В этом нам может помочь теория вероятности.
Глава 3. Выявление возможности применения теории вероятности при определении шанса выиграть в азартных играх
Мы уже выявляли возможность использовать расчеты теории вероятности при определении шанса выиграть в конкретном виде игр. Постольку видов азартных игр колоссальное множество, то следует обратиться к универсальной формуле расчета прибыли, которая выглядит следующим образом:
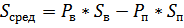
где:
Sсред — средний выигрыш в одном цикле игры (один бросок игральной кости, одно вращение рулетки, одно конкретное действие игрока в покере, одна ставка в букмекерской конторе и т. п.);
Pв — вероятность выигрыша;
Sв — сумма выигрыша;
Pп — вероятность проигрыша;
Sп — сумма проигрыша.
Эта формула достаточна простая, но главное её легко применить в жизни.
К примеру, вы бросаете игральную кость единожды. И для выигрыша нужна сумма меньше 5 очков. Какова будет сумма выигрыша, будет ли он вообще и стоит ли начинать игру?
Всего будет 36 возможных вариантов. После подсчёта видим, что всего 6 раз сумма очков двух костей будет меньше 5. Значит, вероятность выигрыша равна 1/6:
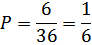
Соответственно, вероятность проигрыша равна 5/6. Также, допустим, мы ставим 10$.
Так, руководствуясь универсальной формулой, следует:
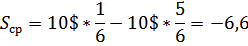
Из этого мы делаем вывод, что, если будем ставим по 10$ каждый раз, то вероятнее всего проиграем 6,6$, а значит это невыгодно и не стоит начинать игру.
Этот пример иллюстрирует одно из многих применений теории вероятности в реальной жизни.
Таким образом, можно подобрать серию задач на уроках математики, которые можно с успехом решать, обсуждать и, возможно, применять в жизни. Кстати, это касается не только азартных игр, но и других случаев, когда нужно делать выбор.
Еще раз подчеркнем, что, если кто решит, что выиграть огромную сумму денег в азартные игры – это легко, он ошибается. Изученный мной материал показывает, что, в принципе, это возможно, но для этого необходимо вести долгие и кропотливые подсчеты. Так что, это тоже огромный труд, а не результат фортуны.
Заключение
Цель и задачи, поставленные в работе, выполнены. В частности, нам удалось рассмотреть теорию вероятности в азартных играх и доказать её универсальность. Узнали, что теория вероятностей – это математическая наука, изучающая закономерности массовых случайных явлений. Она определяет и анализирует числовые характеристики случайных событий, наиболее важными, из которых являются вероятность события и математическое ожидание случайной величины. Также в процессе изучения материала мы познакомились с наиболее интересными видами азартных игр и их классификацией.
Работа позволяет сделать вывод о том, что в основе таких игр лежит математическая наука, как теория вероятности. Благодаря её точным и грамотным вычислениям, можно выяснить какой ход, какое решение или какая ставка возможно принесёт игроку успех.
Также на примерах я выяснила, что:
- выигрыш в азартных играх ничтожно мал и сводится к нулю;
- большинство людей считает, что игра в карты, игровые автоматы, рулетку и т. п. приносят быструю и лёгкую прибыль, хотя это не является истиной.
Мне хотелось бы, чтобы моя работа помогла людям не совершать ошибки, которые они допускают, играя в азартные игры.
Список литературы
1. Бернштейн С.Н. Теория вероятностей, 4 изд.,К. - Л., 2003.








