Глава 1. Универсальность теории вероятности
ВВЕДЕНИЕ
Моя «Применение теории вероятности при определении выигрыша в азартных играх» является очень интересной. Математика соприкасается с обыденной жизнью гораздо больше, чем мы можем себе представить. Эта наука встречается нам каждый день при самых различных ситуациях. Например, вероятность — это одно из основных понятий не только в математической статистике, но и в жизни любого человека. Так каждому из нас каждый день приходится принимать множество решений в условиях неопределенности. Однако эту неопределенность можно «превратить» в некоторую определенность. И тогда это знание может оказать существенную помощь при принятии решения. Как ни странно, но человек часто применяет теорию вероятностей в повседневном быту, хотя может и не знать математические формулы и распределения кривой вероятности, и это не обязательно. Жизненный опыт, логика и интуиция всегда подсказывают человеку его шансы на удачу, будь то поступление на работу, карьера, личная жизнь, решение проблем, возможность выигрыша и т.п. Однако иногда очень полезно проверить совпадают ли догадки с математическим анализом, ведь у каждого «случайного» события есть четкая вероятность его наступления.
Мне хотелось бы обратиться, по большей степени, к азартным играм, а точнее к вероятности выигрыша в них. Ведь азартные игры уже давно представляют развлекательные возможности для людей, чтобы сочетать удачу и мастерство в погоне за прибыльными выигрышами. Существуют сотни различных форм азартных игр, и каждая может определяться определенным математическим принципом.
Почему же люди прибегают к азартным играм? Я думаю, из-за желания получить как можно больше денежных средств и это не является ни для кого секретом. Но ведь у каждой монеты есть две стороны. Поэтому чтобы действительно выиграть, а не проиграть и не стать банкротом, в азартных играх нужны знания и удача. Конечно, без фортуны тяжело надеяться на благоприятный исход событий, однако больший, я бы даже сказала основной, является фактор умения применять математические знания или же теорию вероятности.
Итак, передо мной стоит следующая проблема: являются ли азартные игры действительно лёгким, доступным и подходящим методом для увеличения своего богатства?
Цель данной исследовательской работы заключается в изучении возможности применения теории вероятности при определении шанса выигрыша в азартных играх.
Также есть следующие задачи, которые необходимо выполнить в ходе исследовательской работы:
· Показать универсальность теории вероятности
· Провести вероятностный анализ азартных игр
· Выявить возможности применения теории вероятности при определении шанса выигрыша в азартных играх.
В процессе проведения исследования мною использовались преимущественно теоретические методы исследования: анализ, синтез, моделирование, классификация, обобщение, сравнение.
Мое исследование носит также преимущественно познавательный, чем прикладной характер. Однако некоторые выводы и собранный материал может быть использован на уроках математики при изучении тем, связанных с теорией вероятности.
Глава 1. Универсальность теории вероятности
Чтобы разобраться непосредственно в теории вероятности и расчётах, давайте для начала обратимся к истории её появления.
Французский дворянин, некий господин де Мере, был азартным игроком в кости и страстно хотел разбогатеть. Он затратил много времени, чтобы открыть тайну игры в кости. Он выдумывал различные варианты игры, предполагая, что таким образом приобретет крупное состояние. Так, например, он предлагал бросать одну кость по очереди 4 раза и убеждал партнера, что, по крайней мере, один раз выпадет при этом шестерка. Если за 4 броска шестерка не выходила, то выигрывал противник.
В те времена еще не существовала отрасль математики, которую сегодня мы называем теорией вероятностей, а поэтому, чтобы убедиться, верны ли его предположения, господин Мере обратился к своему знакомому, известному математику и философу Б. Паскалю с просьбой, чтобы он изучил два знаменитых вопроса, первый из которых он попытался решить сам.
Вопросы были следующие:
Сколько раз надо бросать две игральные кости, чтобы случаев выпадения сразу двух шестерок было больше половины от общего числа бросаний?
Как справедливо разделить поставленные на кон двумя игроками деньги, если они по каким-то причинам прекратили игру преждевременно?
Также в письме к Паскалю он пишет: «Вы знаете, что я открыл редкие вещи, которые почтенные математики никогда не обсуждали. О моих открытиях писали Вы, Ферма и Гюйгенс, которые ими восхищались. Эта наука имеет много любопытных вещей, но которые мне кажутся не очень полезными»[1].
Паскаль не только сам заинтересовался этим, но и написал письмо известному математику П. Ферма, чем спровоцировал его заняться общими законами игры в кости и вероятностью выигрыша.
Таким образом, азарт и жажда разбогатеть дали толчок возникновению новой чрезвычайно существенной математической дисциплины: теории вероятностей. В разработке ее основ принимали участие математики такого масштаба, как Паскаль и Ферма, Гюйгенс, который написал тракта «О расчетах при азартных играх», Яков Бернулли, Муавр, Лаплас, Гаусс и Пуассон. В наше время теория вероятности используется почти во всех отраслях знаний: в статистике, синоптике (прогноз погоды), биологии, экономике, технологии, строительстве и т. д.
Все мы в той или иной мере используем теорию вероятности на основе анализе произошедших в нашей жизни событий. Например, мы знаем, что смерть во время автомобильной аварии боле вероятна, чем от удара молнии, потому что первое, к сожалению, происходит очень часто. Так или иначе, мы обращаем на вероятность вещей внимание, чтобы спрогнозировать свое поведение. Но, к сожалению, не всегда человек может точно определить вероятность тех или иных событий.
Например, не зная статистики, большинство людей склонны думать, что шанс погибнуть в авиакатастрофе больше, чем в автомобильной аварии. Теперь же мы знаем, изучив факты (о которых, думаю, многие наслышаны), что это совсем не так. Дело в том, что наш жизненный «глазомер» иногда дает сбой, потому что авиатранспорт кажется значительно страшнее людям, привыкшим твердо ходить по земле. Да и большинство людей не так часто используют этот вид транспорта. Даже если мы и может оценить вероятность события верно, то, скорее всего, крайне неточно, что не будет иметь никакого смысла, скажем, в космической инженерии, где миллионные доли решают многое. А когда нам нужна точность, то мы обращаемся к кому? Конечно же, к математике.
Примеров реального использования теории вероятности в жизни множество. Практически вся современная экономика базируется на ней. Выпуская на рынок определенный товар, грамотный предприниматель наверняка учтет риски, а также вероятности покупки в том или рынке, стране и т.д. Практически не представляют свою жизнь без теории вероятности брокеры на мировых рынках. Предсказывание денежного курса (в котором точно не обойтись без теории вероятности) на денежных опционах или знаменитейшем рынке Forex дает возможность зарабатывать на данной теории серьезные деньги.
Теория вероятности имеет значение в начале практически любой деятельности, а также ее регулирования. Благодаря оценке шансов той или иной неполадки (например, космического корабля), мы знаем, какие усилия нам нужно приложить, что именно проверить, что вообще ожидать в тысячи километров от Земли. Возможности теракта в метрополитене, экономического кризиса или ядерной войны — все это можно выразить в процентах. А главное, предпринимать соответствующие контрдействия исходя из полученных данных. Любую деятельность любой сферы можно проанализировать, использую статистику, рассчитать благодаря теории вероятности и заметно улучшить.
В азартных играх теория вероятностей – расчет с использованием специальных формул. Подсчитывать в уме или на бумажке возможность выпадения той или иной комбинации в слоте долго и бессмысленно. То же можно сказать и о рулетке, покере. Специалисты создали программы, производящие необходимые подсчеты на основе заданных данных – предыдущих результатов игры. Прежде чем подсчитать вероятность победы, необходимо заняться фиксацией важной информации и записать, сколько раз выпадало определенное число на рулетке, как часто слот выдавал денежные призы и т.д.
Рассчитывать выигрышные комбинации, опираясь на теорию вероятностей, можно лишь в случае, если казино придерживается принципов честной игры. При вмешательстве в работу автоматов со стороны оператора предугадать исход событий невозможно.
Таким образом, мы чётко прослеживаем связь между теорией вероятностей и азартными играми.
Уже так много было сказано о теории вероятности, но что же это такое?
Теория вероятностей – это наука о закономерностях случайных событий. Под случайным событием в теории вероятностей понимается всякое явление, которое может произойти или не произойти (случайным образом) при осуществлении определенного комплекса условий. Каждое такое осуществление называется испытанием, опытом или экспериментом[2].
События можно подразделить на достоверные, невозможные и случайные.
Достоверным называется событие, которое обязательно произойдет при испытании. Невозможным называется событие, которое заведомо не произойдет при испытании. Случайным называется событие, которое в результате эксперимента может либо произойти, либо не произойти (в зависимости от случайных обстоятельств)[3].
Предметом теории вероятностей являются закономерности массовых случайных событий, где под массовостью мы понимаем многократную повторяемость[4].
Рассмотрим несколько событий:
появление герба при бросании монеты;
появление трех гербов при трехкратном бросании монеты;
попадание в цель при выстреле;
выигрыш по билету денежно-вещевой лотереи.
Очевидно, что каждое из этих событий обладает какой-то степенью возможности. Для того, чтобы количественно сравнивать между собой события по степени возможности, нужно с каждым событием связать определенное число.
Вероятность события есть численная мера степени объективной возможности этого события. В качестве единицы измерения вероятности принята вероятность достоверного события. Вероятность невозможного события равна нулю. Вероятность любого случайного события обозначается P и изменяется в диапазоне от нуля до единицы: 0 ≤ P ≤ 1.
Вероятностью случайного события называется отношение числа n несовместимых равновероятных элементарных событий, составляющих событие, к числу всех возможных элементарных событий N:
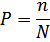
Одной из важнейших задач теории вероятностей является выявление практически невозможных (или практически достоверных) событий, дающих возможность предсказывать результат опыта, и выявление условий, при которых те или иные события становятся практически невозможными (достоверными)[5].
Наряду с практически невозможными (достоверными) событиями, которые позволяют с уверенностью предсказывать исход опыта, несмотря на наличие случайности, в теории вероятностей большую роль играют особого типа случайные величины, которые, хотя и являются случайными, но имеют такие незначительные колебания, что практически могут рассматриваться как не случайные. Примером такой «почти не случайной» величины может служить частота события при большом числе опытов. Эта величина хоть и является случайной, но при большом числе опытов практически может колебаться только в очень узких пределах вблизи вероятности события.
Такие «почти не случайные» величины дают возможность предсказывать численный результат опыта, несмотря на наличие в нем элементов случайности, оперируя с этим результатом столь же уверенно, как мы оперируем с данными, которые доставляются обычными методами точных наук.
Так, доказывается универсальность теории вероятности. Также мы можем сделать вывод, что методы, которые используются при расчетах в теории вероятности вполне применимы и в практической жизни каждого человека. Для этого вовсе не нужно использовать сложные расчеты, а нужно всего лишь фиксировать и анализировать определенную последовательность данных. Изучая на уроках темы, связанные с теорией вероятности (отдельные ее элементы, конечно) я приучилась быть более наблюдательной и тщательно подходить к анализу происходящих событий. Также это помогает мне принимать решения при планировании тех или иных действий. Таким образом, я считаю, что теория вероятности, действительно, универсальна и ее может использовать каждый школьник, если ему более детально и интересно объяснить, как это делать. В том числе, представляет, конечно же, интерес возможности использования теории вероятности в азартных играх для того, чтобы разбогатеть. А стать богатым в наше время хочет каждый. И это правильно в условиях рыночной экономики и постиндустриального общества, в котором мы живем. Поэтому, я считаю, что, если приводить примеры из азартных игр, то можно заинтересовать учеников в изучении теории вероятности. Как же может помочь эта теория в возможности выиграть в азартные игры? Рассмотрим этот вопрос подробнее в следующей главе.








