1.1. Характеристики и параметры фильтров. 3
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ
ЮЖНОГО ФЕДЕРАЛЬНОГО УНИВЕРСИТЕТА В г. ТАГАНРОГЕ
ИНСТИТУТ РАДИОТЕХНИЧЕСКИХ СИСТЕМ И УПРАВЛЕНИЯ
КАФЕДРА СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Курсовой проект
на тему:
«Фильтры верхних частот»
по курсу
Электроника
Выполнил:
студент группы Ртбо3-8
Антипин С.О.
____________
Проверил:
Христич В. В.
«__» ____________ 2014г.
Таганрог 2014 г.
СОДЕРЖАНИЕ:
1. ВВЕДЕНИЕ.. 3
1.1. Характеристики и параметры фильтров. 3
1.2. Конструирование функций передачи фильтров. 4
1.3. Синтез базовой матрицы низкочувствительных фильтров. 7
2. КОНВЕРТОРНЫЕ ФИЛЬТРЫ... 8
2.1. Синтез лестничных LC-фильтров. 8
2.2. Конверторные фильтры нижних и верхних частот. 11
2.3. Полосовые конверторные фильтры.. 14
5. РАСЧЕТ ЭЛЕМЕНТОВ.. 16
6. ПРИНЦИПИАЛЬНАЯ СХЕМА.. 17
7. АНАЛИЗ СХЕМЫ... 18
8. МЕТОД МОНТЕ-КАРЛО.. 21
9. ВЫБОР ТИПОВ ЭЛЕМЕНТОВ.. 23
10. ВЫВОД.. 24
11. СПИСОК ИСПОЛЬЗЕМОЙ ЛИТЕРАТУРЫ... 25
1. ВВЕДЕНИЕ
1.1. Характеристики и параметры фильтров
В общем случае электрический фильтр – это цепь с заданной реакцией на данное воздействие. Под частотным фильтром понимается устройство, пропускающее сигналы одних частот и задерживающее сигналы других частот. Область частот, в которой сигналы пропускаются фильтром, называется полосой пропускания, а в которой задерживаются – полосой режекции. Между полосой пропускания и полосой режекции расположена переходная область.
Взаимное положение полос пропускания и режекции является классификационным признаком различных типов фильтров. По этому признаку фильтры подразделяются на ФНЧ – фильтры нижних частот, ФВЧ – фильтры верхних частот, ПФ – полосовые фильтры и РФ – режекторные фильтры. Общий вид их амплитудно-частотных характеристик (АЧХ) показан на рис. 1.1. Они могут быть как колебательными (в частности, равноволновыми), так и монотонными (на рис. 1.1 изображены равноволновые АЧХ), причем не обязательно одинаковой формы в полосах пропускания и режекции. Нижняя и верхняя граничные частоты полосы пропускания (
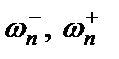 ) и полосы режекции (
) и полосы режекции ( 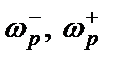 ) являются параметрами фильтра (у полосового фильтра две полосы режекции, а у режекторного – две полосы пропускания). В пределах полосы пропускания модуль функции передачи фильтра
) являются параметрами фильтра (у полосового фильтра две полосы режекции, а у режекторного – две полосы пропускания). В пределах полосы пропускания модуль функции передачи фильтра 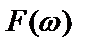 должен быть постоянен с заданной величиной ошибки
должен быть постоянен с заданной величиной ошибки 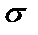 , а в пределах полосы режекции не должен превышать некоторого малого значения
, а в пределах полосы режекции не должен превышать некоторого малого значения 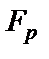 . Параметр
. Параметр
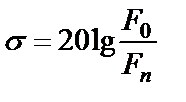
называется неравномерностью амплитудно-частотной характеристики в полосе пропускания, а
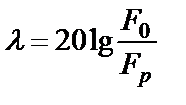
– гарантированным затуханием в полосе режекции ( 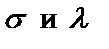 измеряются в децибелах). Чем уже переходная область между полосой пропускания и полосой режекции, тем выше селективность (избирательность) фильтра, т.е. тем меньше (ближе к единице) коэффициент прямоугольности (
измеряются в децибелах). Чем уже переходная область между полосой пропускания и полосой режекции, тем выше селективность (избирательность) фильтра, т.е. тем меньше (ближе к единице) коэффициент прямоугольности ( 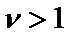 ), который для разных типов фильтров имеет следующие выражения:
), который для разных типов фильтров имеет следующие выражения:
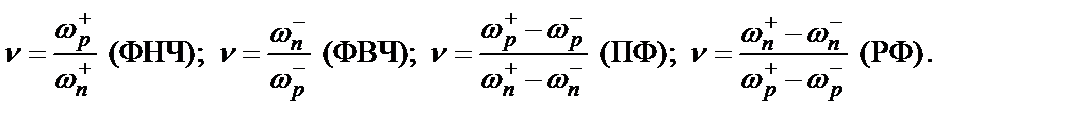
Стабильность (неизменность) амплитудно-частотной характеристики фильтра зависит как от стабильности параметров схемных элементов, так и степени их влияния на АЧХ, что оценивается коэффициентами параметрической чувствительности АЧХ в полосе пропускания и полосе режекции:
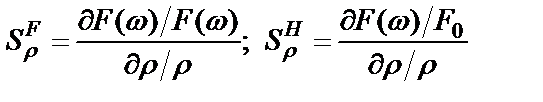 ,
,
где 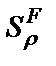 – относительная чувствительность АЧХ в полосе пропускания;
– относительная чувствительность АЧХ в полосе пропускания; 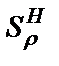 – полуотносительная чувствительность АЧХ в полосе режекции;
– полуотносительная чувствительность АЧХ в полосе режекции; 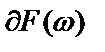 – приращение модуля функции передачи при бесконечно малом относительном приращении (
– приращение модуля функции передачи при бесконечно малом относительном приращении ( 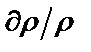 ) параметра
) параметра 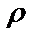 i-го схемного элемента;
i-го схемного элемента; 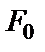 – номинальный (максимальный) коэффициент передачи фильтра в полосе пропускания.
– номинальный (максимальный) коэффициент передачи фильтра в полосе пропускания.
Чтобы оценить дестабилизирующее действие всех элементов схемы используется или матрица чувствительностей, или коэффициенты многопараметрической чувствительности в полосе пропускания и полосе режекции:
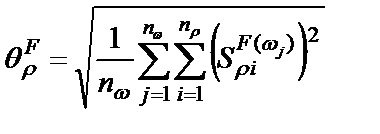 ;
; 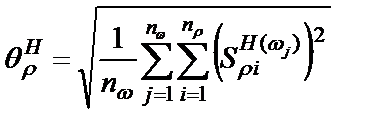 ,
,
где 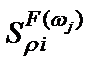 и
и 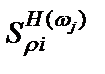 – чувствительности АЧХ на частоте
– чувствительности АЧХ на частоте 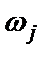 к i -му схемному элементу соответственно в полосе пропускания и полосе режекции (
к i -му схемному элементу соответственно в полосе пропускания и полосе режекции ( 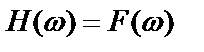 );
); 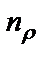 – число дестабилизирующих элементов;
– число дестабилизирующих элементов; 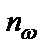 – число точек частотного диапазона анализа.
– число точек частотного диапазона анализа.
Эти меры чувствительности удобно использовать на этапе синтеза различных структур фильтров и их вариантов. На этапе проектирования промышленных образцов используются статистические меры оценки стабильности характеристик фильтров. Статистические характеристики спроектированного изделия определяются методом Монте-Карло.
По характеру влияния на стабильность активного RC-фильтра все его пассивные элементы можно разделить на две группы. К первой группе относятся элементы, в основном определяющие положение нулей и полюсов передаточной функции фильтра и характеризующие значения постоянных времени звеньев. Эти элементы оказывают доминирующее влияние на стабильность фильтра, причем тем большее, чем выше его селективность. Ко второй группе относятся элементы, определяющие коэффициенты передачи звеньев с различных входов. Поскольку коэффициенты передачи звеньев характеризуются отношением параметров однотипных элементов (резисторов) и чувствительность АЧХ к этим элементам не зависит от селективных свойств фильтра, степень их влияния на стабильность АЧХ вторична и при оптимизации чувствительности чаще всего не учитывается.
Активный RC-фильтр, как и другие линейные электронные устройства, может работать только в определенном диапазоне входных (выходных) напряжений, т.е. в определенном динамическом диапазоне
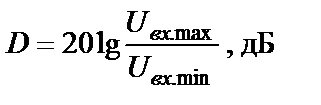 ,
,
нижний уровень ( 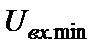 ) которого ограничен величиной шумов электронных компонентов, а верхний уровень (
) которого ограничен величиной шумов электронных компонентов, а верхний уровень ( 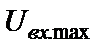 ) – допустимыми нелинейными искажениями сигнала, возникающими в результате перегрузки усилителей, являющихся компонентами активного RC-фильтра.
) – допустимыми нелинейными искажениями сигнала, возникающими в результате перегрузки усилителей, являющихся компонентами активного RC-фильтра.
Динамический диапазон уменьшается, если ограничения сигнала (динамические перегрузки) наступают во внутренних узлах схемы раньше, чем на выходе фильтра. Поэтому при синтезе фильтра предусматривается оптимизация максимальных коэффициентов передачи с входа фильтра в критические узлы его схемы.
1.2. Конструирование функций передачи фильтров
На начальном этапе синтеза фильтра решается задача аппроксимации его амплитудно-частотной характеристики, заданной в виде требований к рабочим параметрам 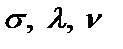 и, реже, к форме АЧХ. Решением задачи аппроксимации является функция передачи некоторой цепи минимального порядка, удовлетворяющей заданным требованиям и условиям физической реализуемости. Передаточные функции могут конструироваться как аналитическим, так и численными методами в зависимости от наличия или отсутствия дополнительных требований к форме АЧХ, например таких, как многополосность или ограниченность полосы (полос) пропускания (режекции), что отличает эти АЧХ от стандартных, показанных на рис. 1.1. При наличии дополнительных требований к форме АЧХ используются численные методы, обладающие большими возможностями, а при их отсутствии (на практике это наиболее часто встречающийся случай) – аналитический метод.
и, реже, к форме АЧХ. Решением задачи аппроксимации является функция передачи некоторой цепи минимального порядка, удовлетворяющей заданным требованиям и условиям физической реализуемости. Передаточные функции могут конструироваться как аналитическим, так и численными методами в зависимости от наличия или отсутствия дополнительных требований к форме АЧХ, например таких, как многополосность или ограниченность полосы (полос) пропускания (режекции), что отличает эти АЧХ от стандартных, показанных на рис. 1.1. При наличии дополнительных требований к форме АЧХ используются численные методы, обладающие большими возможностями, а при их отсутствии (на практике это наиболее часто встречающийся случай) – аналитический метод.
При использовании аналитического метода задача аппроксимации решается не для конкретного типа фильтра, а для некоторого ФНЧ-прототипа, переход к которому осуществляется путем частотного преобразования вида
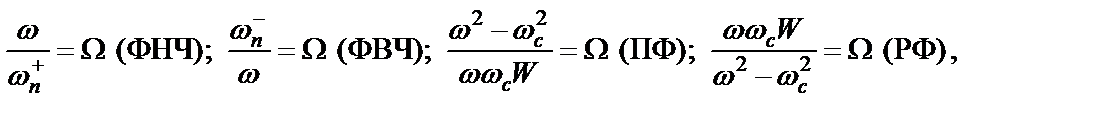
где 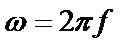 – текущая частота АЧХ реального фильтра;
– текущая частота АЧХ реального фильтра;  – текущая нормированная частота АЧХ ФНЧ-прототипа;
– текущая нормированная частота АЧХ ФНЧ-прототипа; 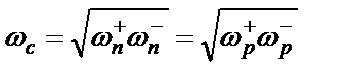 – центральная частота ПФ (РФ);
– центральная частота ПФ (РФ); 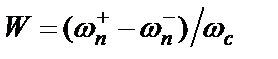 – относительная ширина полосы пропускания ПФ (РФ).
– относительная ширина полосы пропускания ПФ (РФ).
При переходе к ФНЧ-прототипу от полосового или режекторного фильтра предполагается, что у последних амплитудно-частотная характеристика симметрична в геометрическом смысле, т.е. у такой характеристики любая пара частот 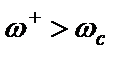 и
и 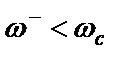 , на которых коэффициенты передачи
, на которых коэффициенты передачи 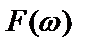 одинаковы, подчиняется закону
одинаковы, подчиняется закону 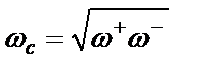 (на практике тип симметрии АЧХ часто не имеет значения, поэтому выбирается геометрическая симметрия, при которой получается более простая реализация).
(на практике тип симметрии АЧХ часто не имеет значения, поэтому выбирается геометрическая симметрия, при которой получается более простая реализация).
В результате указанного частотного преобразования АЧХ любого типа фильтра (см. рис. 1.1) приводится к нормированной АЧХ, показанной на рис. 1.2, где
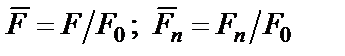 ;
; 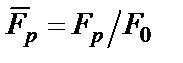 . При этом как форма АЧХ (колебательная или монотонная), так и значения параметров
. При этом как форма АЧХ (колебательная или монотонная), так и значения параметров 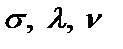 исходного фильтра не изменяются. Чтобы решить задачу аппроксимации, математическое выражение АЧХ ФНЧ-прототипа записывается в такой форме:
исходного фильтра не изменяются. Чтобы решить задачу аппроксимации, математическое выражение АЧХ ФНЧ-прототипа записывается в такой форме:
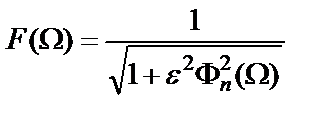 , (1.1)
, (1.1)
где 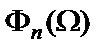 – аппроксимирующая функция n-го порядка (полином или дробь), нормированная таким образом, чтобы на частоте
– аппроксимирующая функция n-го порядка (полином или дробь), нормированная таким образом, чтобы на частоте 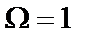 она равнялась единице, т.е.
она равнялась единице, т.е. 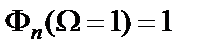 ;
; 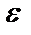 – параметр, характеризующий неравномерность АЧХ на границе полосы пропускания:
– параметр, характеризующий неравномерность АЧХ на границе полосы пропускания: 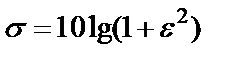 .
.
В качестве 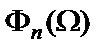 используются специальные функции, наилучшим образом приближающиеся к нулю на интервале
используются специальные функции, наилучшим образом приближающиеся к нулю на интервале 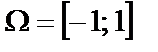 и резко возрастающие (по модулю) вне этого интервала, что важно, поскольку такие свойства
и резко возрастающие (по модулю) вне этого интервала, что важно, поскольку такие свойства 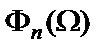 определяют высокую селективность синтезируемого фильтра. Среди полиномиальных функций этим требованиям в наибольшей степени отвечает полином Чебышева
определяют высокую селективность синтезируемого фильтра. Среди полиномиальных функций этим требованиям в наибольшей степени отвечает полином Чебышева
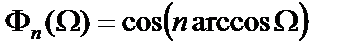 при
при 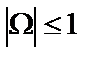 ,
, 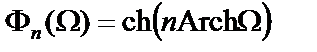 при
при 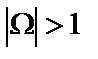 ,
,
а среди дробных функций – дробь Золотарева, являющаяся наилучшей по критерию селективности. Дробь Золотарева – это частный случай дроби Чебышева
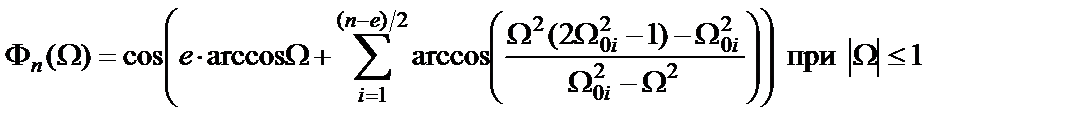 , (1.2)
, (1.2)
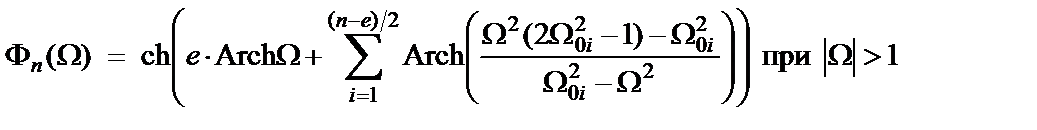 ,
,
полюсы 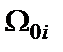 которой выбраны из условия изоэкстремальности характеристики дроби
которой выбраны из условия изоэкстремальности характеристики дроби 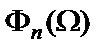 в диапазоне переменной
в диапазоне переменной 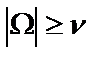 (
( 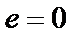 при n четном,
при n четном, 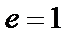 при n нечетном). Оптимальные в этом смысле значения полюсов
при n нечетном). Оптимальные в этом смысле значения полюсов 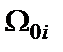 обычно вычисляются через эллиптические функции Якоби, однако их можно определить и методом последовательных приближений. В последнем случае процедура отыскания
обычно вычисляются через эллиптические функции Якоби, однако их можно определить и методом последовательных приближений. В последнем случае процедура отыскания 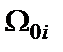 выглядит следующим образом: вначале задаются большие значения
выглядит следующим образом: вначале задаются большие значения 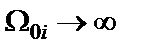 и вычисляются нули
и вычисляются нули 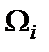 функции (1.2), затем принимается
функции (1.2), затем принимается 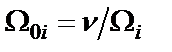 и вновь определяются нули
и вновь определяются нули 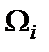 функции (1.2), и так до тех пор, пока последующие значения
функции (1.2), и так до тех пор, пока последующие значения 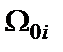 не будут отличаться от предыдущих на величину допустимой ошибки. У фильтров с аппроксимацией дробью Золотарева (фильтров Золотарева–Кауэра) амплитудно-частотная характеристика является равноволновой как в полосе пропускания, так и в полосе режекции, а у фильтров с аппроксимацией полиномом Чебышева (фильтров Чебышева) – равноволновой в полосе пропускания и монотонной в полосе режекции.
не будут отличаться от предыдущих на величину допустимой ошибки. У фильтров с аппроксимацией дробью Золотарева (фильтров Золотарева–Кауэра) амплитудно-частотная характеристика является равноволновой как в полосе пропускания, так и в полосе режекции, а у фильтров с аппроксимацией полиномом Чебышева (фильтров Чебышева) – равноволновой в полосе пропускания и монотонной в полосе режекции.
При четном порядке n фильтра Золотарева асимптотическое значение его коэффициента передачи 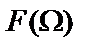 при
при 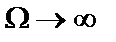 не стремится к нулю, что является недостатком такой аппроксимации и объясняется наличием у дроби Золотарева полного набора конечных полюсов (
не стремится к нулю, что является недостатком такой аппроксимации и объясняется наличием у дроби Золотарева полного набора конечных полюсов ( 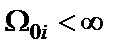 при i =1, 2, … , n/2). Поэтому с целью уменьшения на единицу числа полюсов функции (1.2), т.е. числа нулей функции (1.1), используется преобразование вида
при i =1, 2, … , n/2). Поэтому с целью уменьшения на единицу числа полюсов функции (1.2), т.е. числа нулей функции (1.1), используется преобразование вида
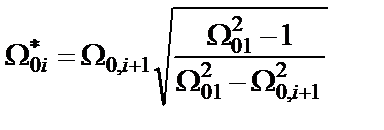 ,
,
где 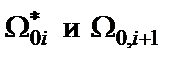 – новое и прежнее значения полюса дроби Золотарева (при этом
– новое и прежнее значения полюса дроби Золотарева (при этом 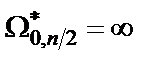 );
); 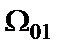 – прежний первый (наибольший) полюс дроби Золотарева. Чтобы сохранить равноволновый характер АЧХ в полосе пропускания и полосе режекции, необходимо преобразовать и нули
– прежний первый (наибольший) полюс дроби Золотарева. Чтобы сохранить равноволновый характер АЧХ в полосе пропускания и полосе режекции, необходимо преобразовать и нули 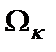 функции (1.2):
функции (1.2):
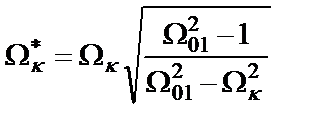 .
.
Фильтры с меньшим на единицу числом нулей передачи, в отличие от фильтров типа a с аппроксимацией (1.2), классифицируются как фильтры типа b. Последующие преобразования полюсов и нулей дроби Чебышева четного порядка
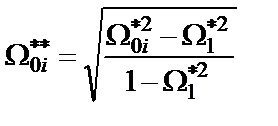 ,
, 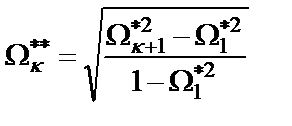
позволяют перейти к фильтрам типа c, которые характеризуются меньшим на единицу числом максимумов АЧХ в полосе пропускания. В этих выражениях 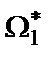 – прежняя наименьшая частота нуля дроби Чебышева.
– прежняя наименьшая частота нуля дроби Чебышева.
В результате решения задачи аппроксимации становятся известными порядок фильтра n, а также значения корней полиномов числителя и знаменателя передаточной функции ФНЧ-прототипа
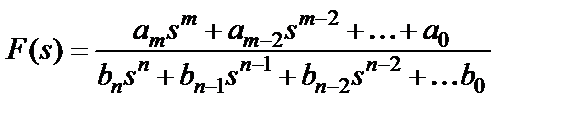 , (1.3)
, (1.3)
где 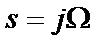 ;
; 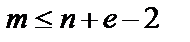 – степень (четная) полинома числителя (при полиномиальной аппроксимации
– степень (четная) полинома числителя (при полиномиальной аппроксимации 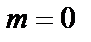 ); n – степень полинома знаменателя, являющегося полиномом Гурвица;
); n – степень полинома знаменателя, являющегося полиномом Гурвица; 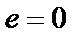 при n четном,
при n четном, 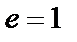 при n нечетном. Степень полинома числителя определяет число нулей передачи, а степень полинома знаменателя – число экстремумов АЧХ в полосе пропускания (при равноволновом характере АЧХ). Для перехода от функции передачи ФНЧ-прототипа (1.3) к функции передачи реального фильтра
при n нечетном. Степень полинома числителя определяет число нулей передачи, а степень полинома знаменателя – число экстремумов АЧХ в полосе пропускания (при равноволновом характере АЧХ). Для перехода от функции передачи ФНЧ-прототипа (1.3) к функции передачи реального фильтра 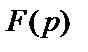 используется соответствующее стандартное частотное преобразование
используется соответствующее стандартное частотное преобразование
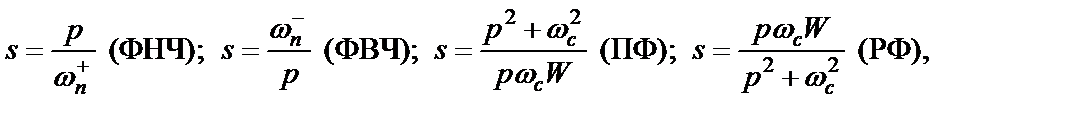 (1.4)
(1.4)
где 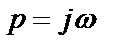 – мнимая частота.
– мнимая частота.
Значения корней полиномов числителя и знаменателя функции 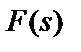 при различных аппроксимирующих функциях
при различных аппроксимирующих функциях 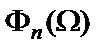 табулированы и приведены в справочниках по расчету фильтров. При конструировании активных RC-фильтров после этапа аппроксимации АЧХ проводится этап синтеза структурной и (или) принципиальной схемы фильтра одним из известных методов, к числу которых, прежде всего, относятся методы имитации лестничных LC -фильтров и метод матричных преобразований (здесь не рассматриваются каскадные фильтры, поскольку их параметрическая чувствительность в несколько раз и даже в десятки раз хуже чувствительности фильтров, синтезированных указанными методами).
табулированы и приведены в справочниках по расчету фильтров. При конструировании активных RC-фильтров после этапа аппроксимации АЧХ проводится этап синтеза структурной и (или) принципиальной схемы фильтра одним из известных методов, к числу которых, прежде всего, относятся методы имитации лестничных LC -фильтров и метод матричных преобразований (здесь не рассматриваются каскадные фильтры, поскольку их параметрическая чувствительность в несколько раз и даже в десятки раз хуже чувствительности фильтров, синтезированных указанными методами).
1.3. Синтез базовой матрицы низкочувствительных фильтров
Метод синтеза базовой матрицы низкочувствительного фильтра
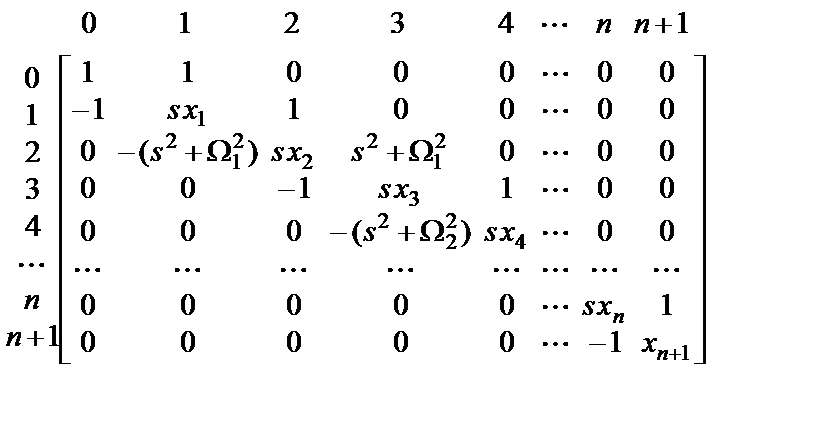 (1.5)
(1.5)
основан на применении разложения функции входного иммитанса в непрерывную (цепную) дробь [1]. В (1.5) 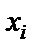 – неизвестные переменные;
– неизвестные переменные; 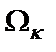 – частота κ-го нуля функции передачи фильтра; n – порядок ФНЧ-прототипа.
– частота κ-го нуля функции передачи фильтра; n – порядок ФНЧ-прототипа.
Для матрицы (1.5) очевидны следующие соотношения между определителем  и алгебраическими дополнениями:
и алгебраическими дополнениями:
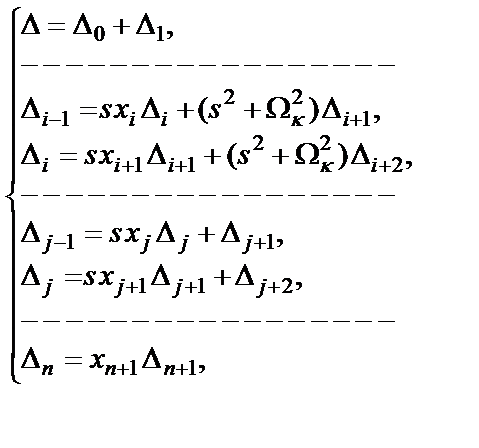
где 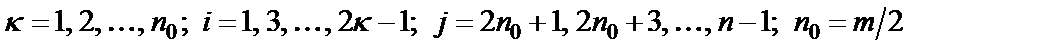 – число нулей передачи;
– число нулей передачи; 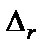 – (r + 1)-кратное алгебраическое дополнение, т.е.
– (r + 1)-кратное алгебраическое дополнение, т.е. 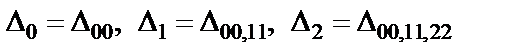 и т. д.
и т. д.
Если вычеркнуть ( 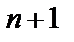 )-ю строку и (
)-ю строку и ( 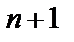 )-й столбец в матрице (1.5), то отношение алгебраических дополнений
)-й столбец в матрице (1.5), то отношение алгебраических дополнений 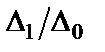 можно рассматривать как входное сопротивление некоторой цепи без потерь. Алгебраические дополнения
можно рассматривать как входное сопротивление некоторой цепи без потерь. Алгебраические дополнения 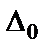 и
и 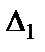 можно выразить через знаменатель
можно выразить через знаменатель 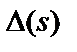 функции передачи
функции передачи 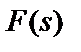 и числитель
и числитель 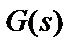 характеристической функции
характеристической функции 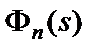 :
:
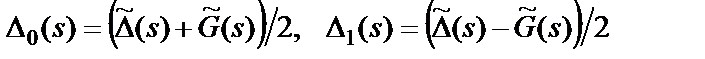 ,
,
где 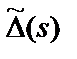 и
и 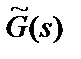 – полиномы, нормированные к коэффициенту при старшем члене.
– полиномы, нормированные к коэффициенту при старшем члене.
Синтез матрицы (1.5) выполняется путем последовательного выделения нулей передачи из функции входного сопротивления:
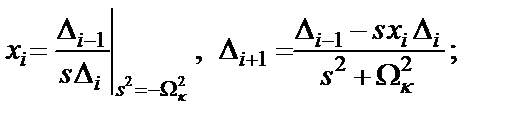
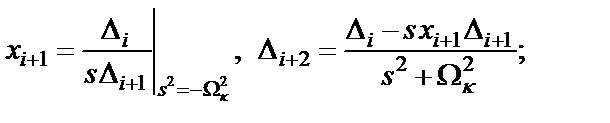
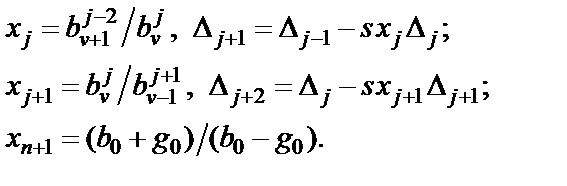
Здесь 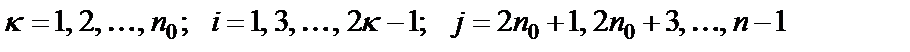 ;
; 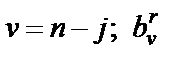 - коэффициент при
- коэффициент при 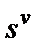 полинома
полинома 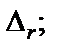
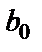 и
и 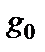 - свободные члены полиномов
- свободные члены полиномов 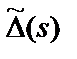 и
и 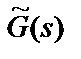 .
.
2. КОНВЕРТОРНЫЕ ФИЛЬТРЫ
2.1. Синтез лестничных LC-фильтров
Конверторные фильтры представляют собой имитационные модели лестничных LC-фильтров, которые отличаются наиболее низкой параметрической чувствительностью.
Матрица иммитансов лестничного LC-ФНЧ-прототипа может быть получена из матрицы (1.5) путем исключения всех четных строк и столбцов. В результате матрица (1.5) для фильтров четного (здесь 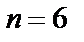 ) и нечетного (здесь
) и нечетного (здесь 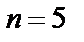 ) примет вид:
) примет вид:
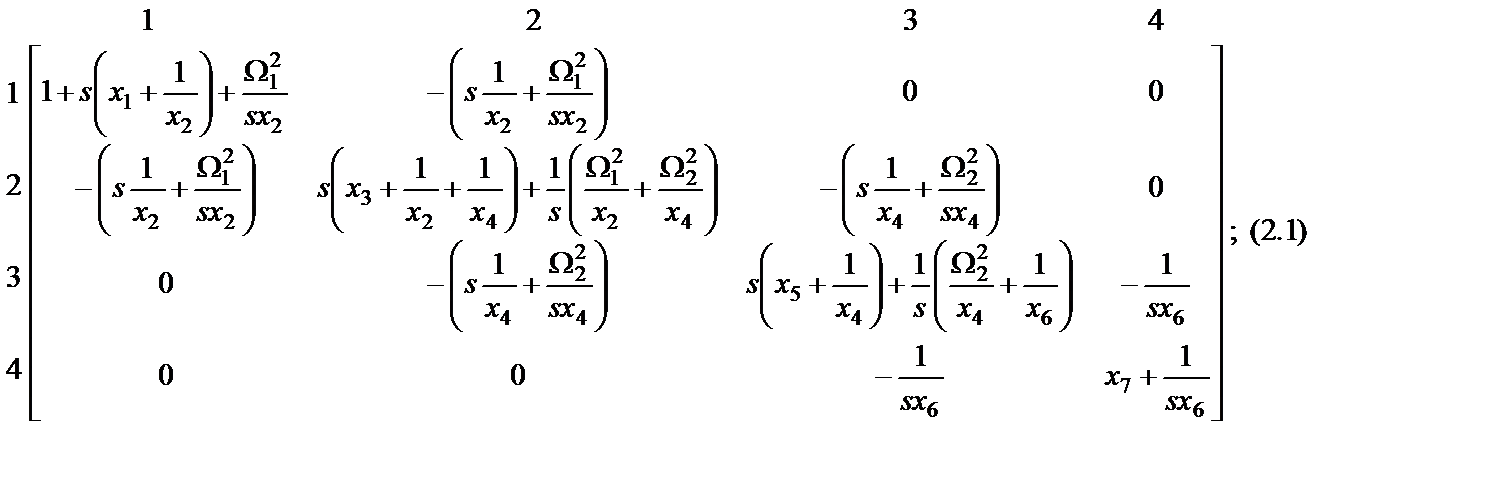
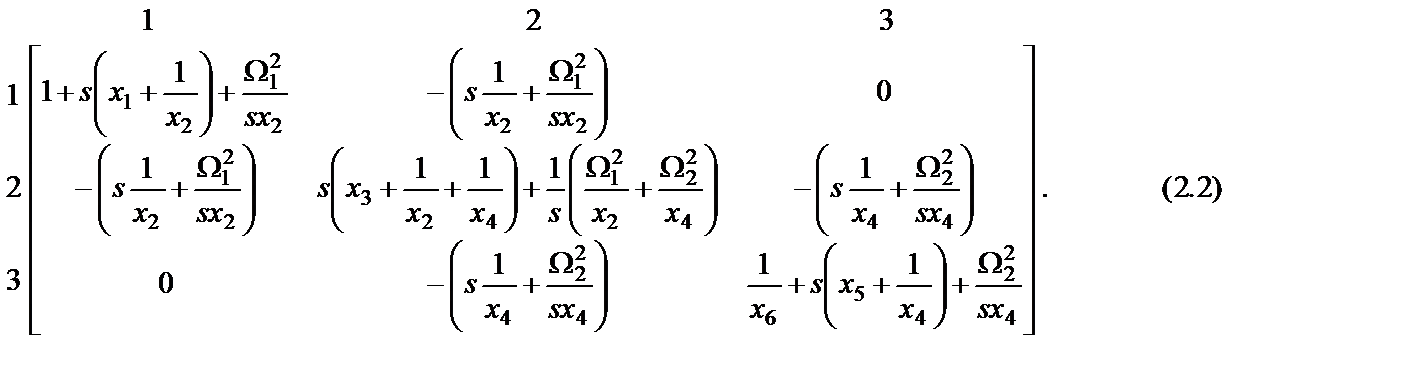
Учитывая, что элементы матрицы (1.5), как и матриц (2.1) и (2.2), величины безразмерные, матрицы (2.1) и (2.2) можно считать или матрицами сопротивлений, или матрицами проводимостей. Полагая, что матрицы (2.1) и (2.2) – это матрицы сопротивлений, им будет соответствовать схема LC-фильтра, изображенная на рис. 2.1,б (схема B). Схема нечетного ( 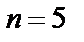 ) порядка, описываемая матрицей сопротивлений (2.2), получается из схемы рис. 2.1,б, если положить
) порядка, описываемая матрицей сопротивлений (2.2), получается из схемы рис. 2.1,б, если положить 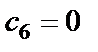 . Соотношения между параметрами элементов схем LC-фильтра типа B и значениями коэффициентов
. Соотношения между параметрами элементов схем LC-фильтра типа B и значениями коэффициентов 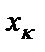 матриц сопротивлений (2.1) и (2.2) имеют вид:
матриц сопротивлений (2.1) и (2.2) имеют вид:
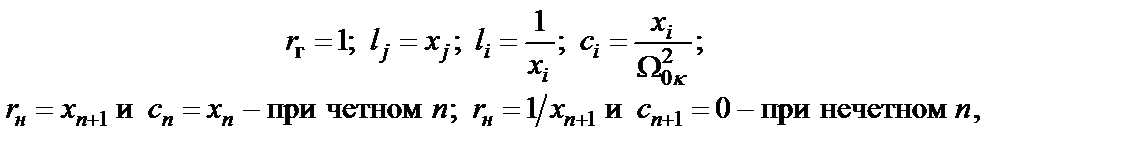 (2.3)
(2.3)
где 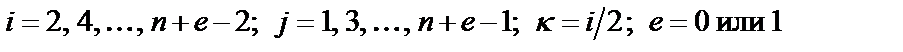 в зависимости от четности или нечетности n.
в зависимости от четности или нечетности n.
Рис. 2.1. Схемы А (а) и В (б) лестничного LC-ФНЧ-прототипа
Если считать матрицы (2.1) и (2.2) матрицами проводимостей, то, после изменения нумерации их строк и столбцов, они будут описывать схему A лестничного LC-фильтра (рис. 2.1,а). В схеме фильтра нечетного порядка (нечетного n) 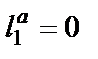 . Соотношения между параметрами элементов схемы А и значениями коэффициентов
. Соотношения между параметрами элементов схемы А и значениями коэффициентов 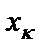 матриц (2.1) и (2.2) имеют вид:
матриц (2.1) и (2.2) имеют вид:
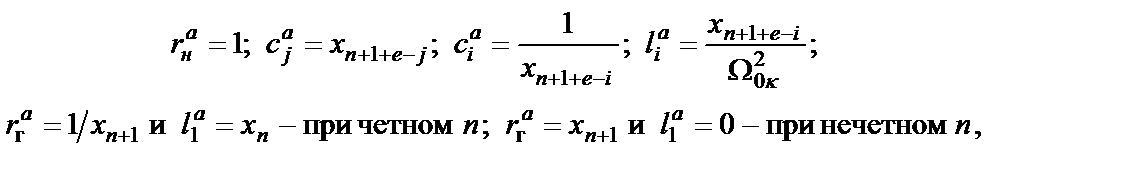 (2.4)
(2.4)
где 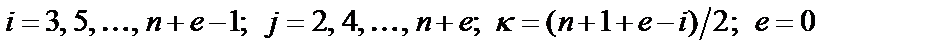 при четном n и
при четном n и 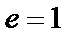 при n нечетном.
при n нечетном.
На основании соотношений (2.3) и (2.4) можно установить соответствия между параметрами элементов схем А и В:
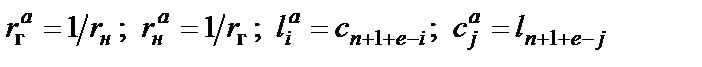 , (2.5)
, (2.5)
где 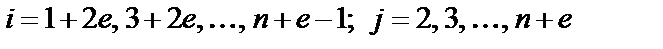 .
.
Нули передачи в схеме рис. 2.1,а реализуются за счет включения параллельно катушкам индуктивности конденсаторов, а в схеме рис. 2.1,б – за счет включения катушек индуктивности последовательно с конденсаторами. У полиномиального лестничного LC-фильтра схемы А и В одинаковы, поскольку у них отсутствуют элементы, обеспечивающие реализацию нулей передачи (конденсаторы с нечетными номерами в схеме А и катушки индуктивности с четными номерами в схеме В).
При переходе от ФНЧ-прототипа к фильтру верхних частот используется стандартное частотное преобразование (1.4), применяемое к проводимостям элементов исходного фильтра:
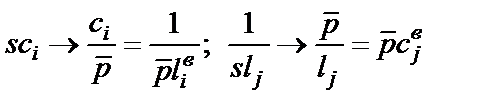
( 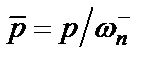 ), что в результате приводит к формальной замене конденсаторов и катушек индуктивности в схеме рис. 2.1 на соответственно катушки индуктивности и конденсаторы (рис. 2.2) с параметрами
), что в результате приводит к формальной замене конденсаторов и катушек индуктивности в схеме рис. 2.1 на соответственно катушки индуктивности и конденсаторы (рис. 2.2) с параметрами
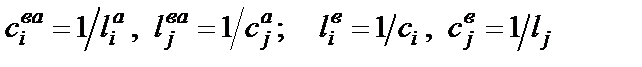 ; (2.6)
; (2.6)
при этом значения сопротивлений резисторов не изменяются:
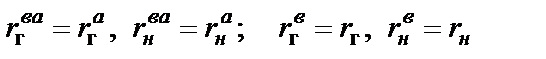 .
.
Рис. 2.2. Схемы А (а) и В (б) лестничного LC-фильтра верхних частот
Переход от ФНЧ-прототипа к полосовому фильтру выполняется путем применения к проводимостям конденсаторов и сопротивлениям катушек индуктивности схемы А стандартного частотного преобразования (1.4):
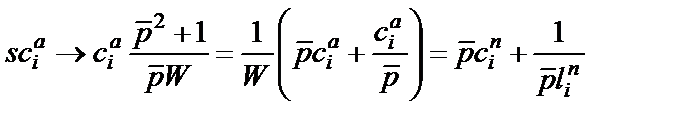 ;
;
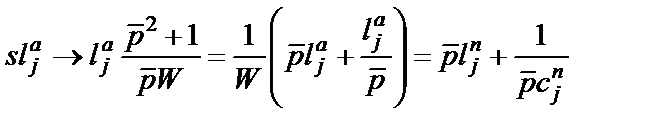
( 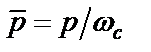 ), результатом чего становится формальная замена каждого конденсатора и каждой катушки индуктивности схемы рис. 2.1,а на соответственно параллельное и последовательное соединение конденсатора и катушки индуктивности, как показано на рис. 2.3.
), результатом чего становится формальная замена каждого конденсатора и каждой катушки индуктивности схемы рис. 2.1,а на соответственно параллельное и последовательное соединение конденсатора и катушки индуктивности, как показано на рис. 2.3.
Рис. 2.3. Полосовой лестничный LC-фильтр 6-го порядка
Применительно к обозначениям, принятым на рис. 2.3, параметры элементов полосового фильтра связаны с параметрами элементов схемы А ФНЧ-прототипа следующими зависимостями:
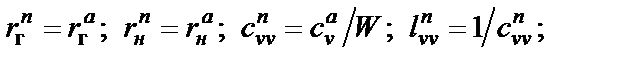
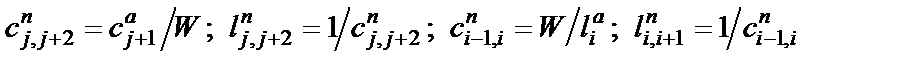 ,
,
где 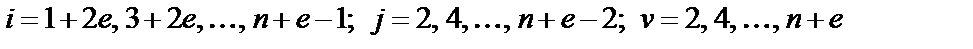 .
.
Учитывая соотношения (2.5) между параметрами элементов схем А и В, можно выразить параметры элементов полосового фильтра через параметры элементов схемы В ФНЧ-прототипа:
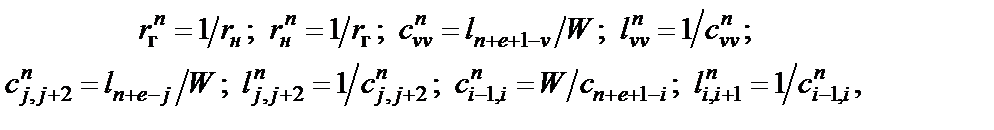 (2.7)
(2.7)
где 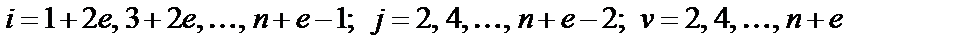 .
.
На рис. 2.3 изображена схема ПФ четного порядка, в отличие от которой в схеме нечетного порядка будут отсутствовать элементы 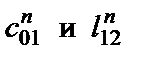 .
.
Матрица проводимостей схемы рис. 2.3 имеет следующий вид:
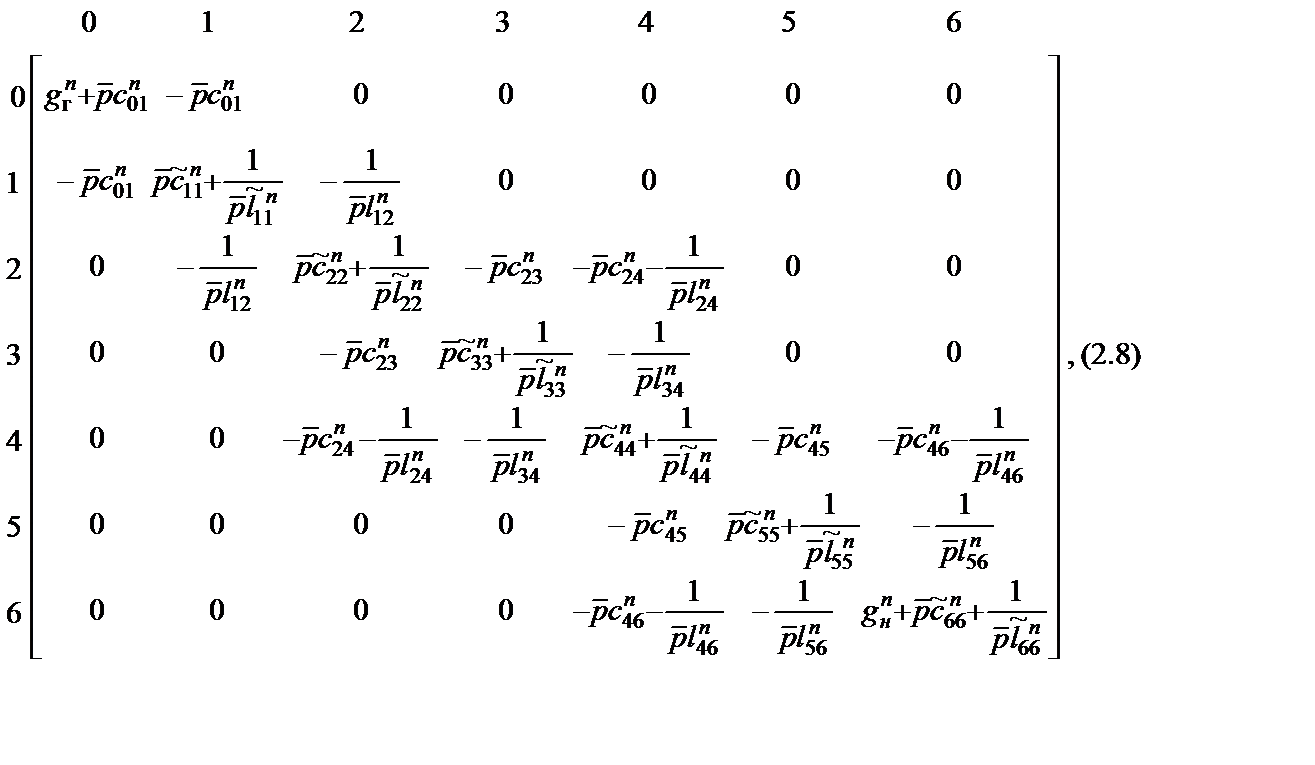
где 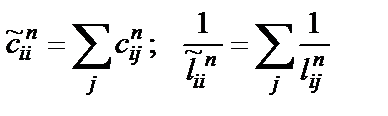 , причем при j < i
, причем при j < i 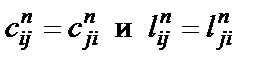 .
.
Если n нечетное, то отсутствуют 0-й и 1-й столбцы, а также 0-я и 1-я строки. При этом элемент на пересечении 2-го столбца и 2-й строки имеет вид 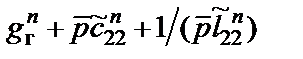 .
.
Как у LC-фильтров, так и у их конверторных моделей наблюдаются динамические перегрузки, когда максимальное напряжение во внутренних узлах схемы превышает максимальное выходное напряжение, что характеризуется коэффициентами динамической перегрузки
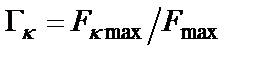 ,
,
где 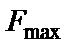 – максимальный коэффициент передачи с входа на выход фильтра;
– максимальный коэффициент передачи с входа на выход фильтра; 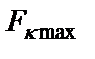 – максимальный коэффициент передачи с входа в κ-й узел схемы.
– максимальный коэффициент передачи с входа в κ-й узел схемы.
Чтобы уменьшить перегрузку в κ-м узле схемы, необходимо в этом узле увеличить проводимость собственных элементов (т.е. элементов, расположенных между этим узлом и общей шиной), а в тех узлах, где 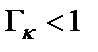 , наоборот, уменьшить. Эти преобразования выполняются таким образом [1], чтобы не изменилась функция передачи фильтра, для чего каждый κ-й столбец и каждую κ-ю строку матрицы проводимостей фильтра умножают на коэффициент
, наоборот, уменьшить. Эти преобразования выполняются таким образом [1], чтобы не изменилась функция передачи фильтра, для чего каждый κ-й столбец и каждую κ-ю строку матрицы проводимостей фильтра умножают на коэффициент
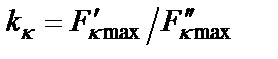 ,
,
где 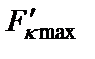 – максимальные значения частных коэффициентов передачи до оптимизации
– максимальные значения частных коэффициентов передачи до оптимизации 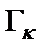 ;
; 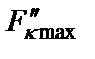 – желаемое (или возможное) значение
– желаемое (или возможное) значение 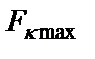 , которое получится после оптимизации
, которое получится после оптимизации 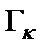 .
.
Поскольку у лестничных ФНЧ и ФВЧ (см. рис. 2.1 и 2.2) собственные элементы узлов только одного типа, оптимизация коэффициентов динамической перегрузки у них невозможна, так как для этого потребовались бы элементы с отрицательными параметрами (емкостями, индуктивностями). У полосовых лестничных LC -фильтров оптимизация 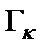 возможна, причем, если выбрать
возможна, причем, если выбрать 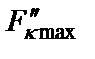 одинаковыми и равными максимальному коэффициенту передачи на выход фильтра, то полностью исключаются перегрузки в κ-х узлах (
одинаковыми и равными максимальному коэффициенту передачи на выход фильтра, то полностью исключаются перегрузки в κ-х узлах ( 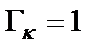 ), но при этом в некоторых случаях и здесь могут потребоваться элементы с отрицательными параметрами. Чтобы избежать применения таких элементов, необходимо изменить значение
), но при этом в некоторых случаях и здесь могут потребоваться элементы с отрицательными параметрами. Чтобы избежать применения таких элементов, необходимо изменить значение 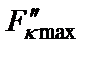 .
.
После оптимизации коэффициентов динамической перегрузки вид матрицы (2.8) не изменится, но элементы матриц 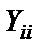 с нечетными i теперь будут содержать и составляющие
с нечетными i теперь будут содержать и составляющие 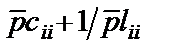 , что означает появление заземленных параллельных LC-контуров в соответствующих узлах схемы рис. 2.3.
, что означает появление заземленных параллельных LC-контуров в соответствующих узлах схемы рис. 2.3.
Применение частотных преобразований (1.4) применительно к LC-фильтрам, как было показано выше, приводит к замене одних реактивных элементов на другие, поэтому преобразования (1.4) называют еще реактансными преобразованиями.
2.2. Конверторные фильтры нижних и верхних частот
Метод синтеза конверторных фильтров – это метод элементной имитации, когда каждый элемент LC-фильтра заменяется элементом или макроэлементом активной RC-техники, базовыми элементами которой являются операционные усилители, резисторы и конденсаторы.
Часто используемым макроэлементом активной RC-техники является конвертор комплексного сопротивления (конвертор сопротивления – КС), одна из наиболее удачных схем которого приведена на рис. 2.4. Он состоит из двух операционных усилителей (ОУ) и четырех пассивных элементов 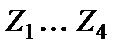 (резисторов и конденсаторов). Конвертор по схеме рис. 2.4 по сравнению с составляющими его операционными усилителями имеет более широкий рабочий частотный диапазон, что объясняется взаимной компенсацией фазовых искажений усилителей ОУ1 и ОУ2. Для случая идеальных ОУ1 и ОУ2 схема рис. 2.4 описывается следующей матрицей проводимостей:
(резисторов и конденсаторов). Конвертор по схеме рис. 2.4 по сравнению с составляющими его операционными усилителями имеет более широкий рабочий частотный диапазон, что объясняется взаимной компенсацией фазовых искажений усилителей ОУ1 и ОУ2. Для случая идеальных ОУ1 и ОУ2 схема рис. 2.4 описывается следующей матрицей проводимостей:
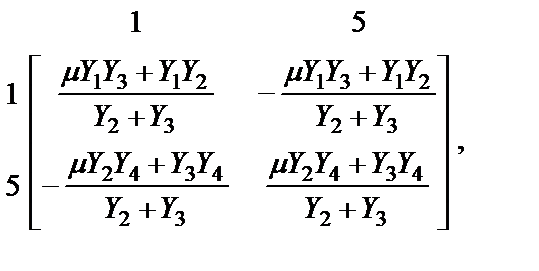 где
где 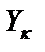 – проводимости элементов КС;
– проводимости элементов КС; 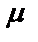 – коэффициенты усиления операционных усилителей.
– коэффициенты усиления операционных усилителей.
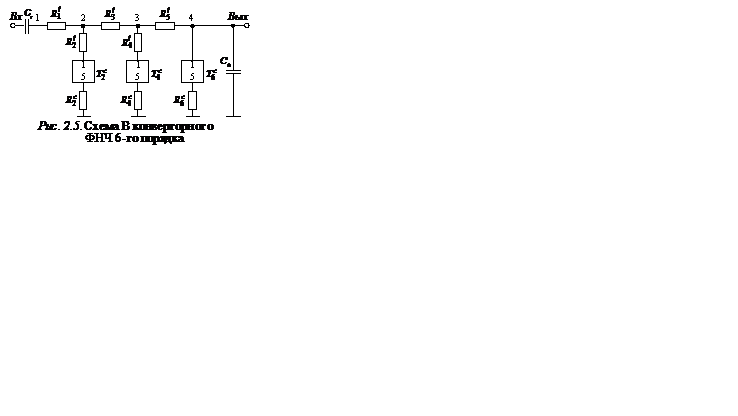
Из выражений матричных элементов следует, что конвертор сопротивления – это невзаимная цепь, реализующая разные проводимости с разных входов (1 или 5), поэтому КС нельзя непосредственно использовать для имитации незаземленной индуктивности. В связи с этим при синтезе фильтра нижних частот схему B LC-ФНЧ-прототипа преобразуют таким образом, чтобы исключить незаземленные элементы, моделируемые с помощью конверторов сопротивления. Для этого проводимости всех элементов схемы B умножают на оператор s, в результате чего изменяется характер проводимостей элементов, и схема приобретает вид, показанный на рис. 2.5, где 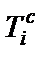 – конвертор сопротивления (рис. 2.4), который совместно с резистором
– конвертор сопротивления (рис. 2.4), который совместно с резистором 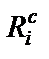 реализует суперемкость
реализует суперемкость 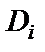 . Выражение проводимости
. Выражение проводимости 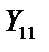 в узле 1 конвертора T, нагруженного на элемент
в узле 1 конвертора T, нагруженного на элемент 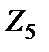 , при
, при 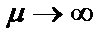 имеет вид
имеет вид
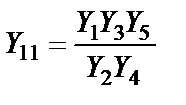 , (2.9)
, (2.9)
где 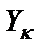 – проводимость κ-го элемента схемы рис. 2.4. Если в схеме конвертора
– проводимость κ-го элемента схемы рис. 2.4. Если в схеме конвертора 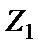 и
и 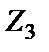 – конденсаторы (
– конденсаторы ( 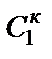 и
и 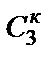 ), а
), а 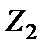 ,
, 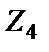 и
и 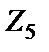 – резисторы (
– резисторы ( 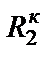 ,
, 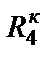 и
и 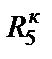 ), то такой D-элемент будет суперемкостью, имеющей проводимость
), то такой D-элемент будет суперемкостью, имеющей проводимость 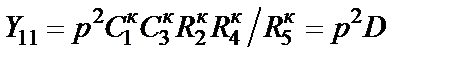 .
.
Поскольку в исходной схеме рис. 2.1,б параметры всех элементов нормированные, для определения реальных параметров элементов схемы рис. 2.5 необходимо вначале перейти от s к p ( 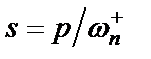 ) и задаться денормирующим сопротивлением
) и задаться денормирующим сопротивлением 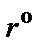 . Тогда
. Тогда
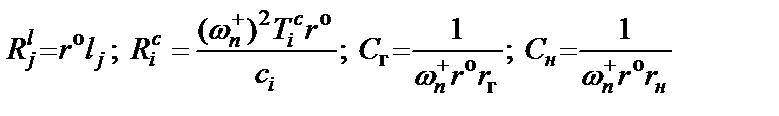 , (2.10)
, (2.10)
где 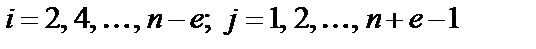 ;
; 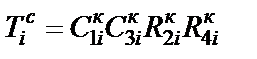 – параметр КС.
– параметр КС.
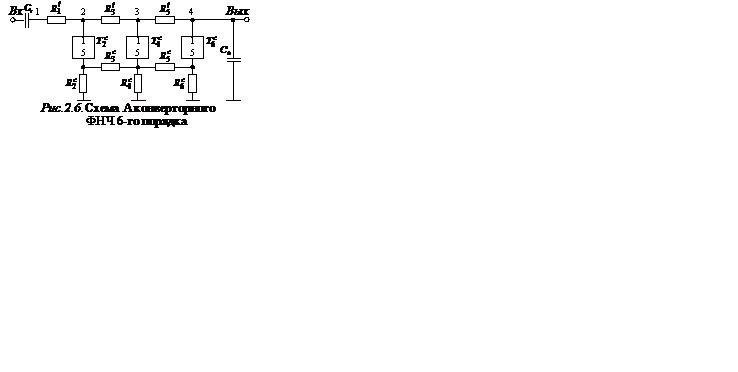 В конверторной модели схемы A лестничного LC-фильтра (рис. 2.6) заземленные суперемкости реализуются конверторами
В конверторной модели схемы A лестничного LC-фильтра (рис. 2.6) заземленные суперемкости реализуются конверторами 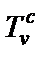 совместно с резисторами
совместно с резисторами 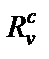 , а незаземленные суперемкости – парой конверторов
, а незаземленные суперемкости – парой конверторов 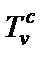 и
и 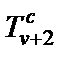 совместно с резисторами
совместно с резисторами 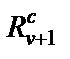 (
( 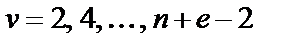 ). Как и в случае схемы B, для определения реальных параметров элементов схемы рис. 2.6 необходимо в выражениях параметров схемы рис. 2.1,а перейти от s к p и задаться денормирующим сопротивлением
). Как и в случае схемы B, для определения реальных параметров элементов схемы рис. 2.6 необходимо в выражениях параметров схемы рис. 2.1,а перейти от s к p и задаться денормирующим сопротивлением 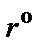 . Поскольку в имитации незаземленных конденсаторов схемы рис. 2.1,а участвуют пары конверторов, необходимо задать для всех конверторов одинаковый параметр
. Поскольку в имитации незаземленных конденсаторов схемы рис. 2.1,а участвуют пары конверторов, необходимо задать для всех конверторов одинаковый параметр 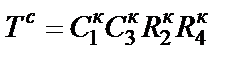 .
.
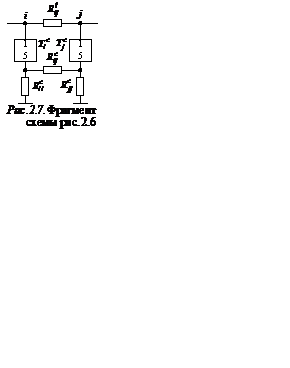
Чтобы идентифицировать параметры элементов схем рис. 2.6 и 2.1,а, необходимо иметь матрицу проводимостей подсхемы, изображенной на рис. 2.7. Такая матрица составляется на основании матрицы проводимостей конвертора сопротивления (см. рис. 2.4) и при 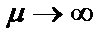 принимает вид
принимает вид
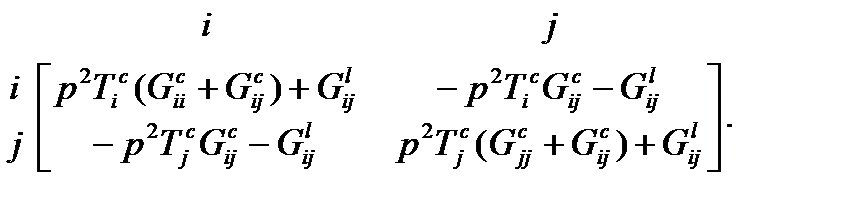
В соответствии с этой матрицей соотношения между параметрами элементов схем рис. 2.6 и рис. 2.1,а имеют следующий вид:
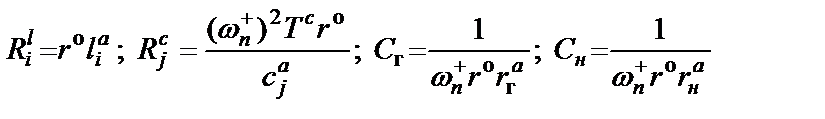 , (2.11)
, (2.11)
где 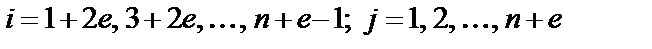 .
.
Так как у конверторного ФНЧ на входе и выходе вместо резисторов используются конденсаторы ( 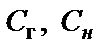 ), путь для постоянного тока неинвертирующего входа ОУ1 конверторов отсутствует, что приводит к большому постоянному напряжению дрейфа нуля ОУ, т.е. фильтр в таком виде неработоспособен. Чтобы уменьшить напряжение дрейфа ОУ, параллельно конденсаторам
), путь для постоянного тока неинвертирующего входа ОУ1 конверторов отсутствует, что приводит к большому постоянному напряжению дрейфа нуля ОУ, т.е. фильтр в таком виде неработоспособен. Чтобы уменьшить напряжение дрейфа ОУ, параллельно конденсаторам 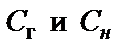 включаются резисторы
включаются резисторы 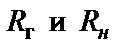 :
:
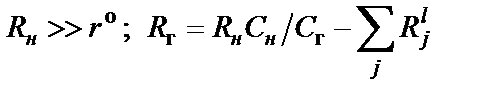 ,
,
где 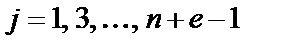 .
.
Включение резисторов 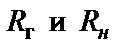 приводит к дополнительным искажениям АЧХ в полосе пропускания, поэтому сопротивление
приводит к дополнительным искажениям АЧХ в полосе пропускания, поэтому сопротивление 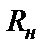 необходимо выбирать как можно больше, но при этом учитывать, что с увеличением
необходимо выбирать как можно больше, но при этом учитывать, что с увеличением 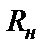 возрастает и паразитное постоянное напряжение на выходе фильтра, т.е. требуется разумный компромисс при выборе величины
возрастает и паразитное постоянное напряжение на выходе фильтра, т.е. требуется разумный компромисс при выборе величины 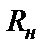 .
.
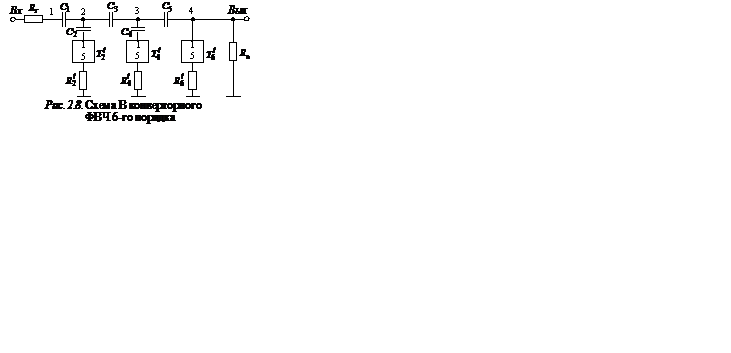 В схеме В лестничного ФВЧ (см. рис. 2.2,б) все катушки индуктивности заземлены, поэтому они могут быть непосредственно реализованы макроэлементами на основе конверторов сопротивления (см. рис. 2.4), если в качестве элементов
В схеме В лестничного ФВЧ (см. рис. 2.2,б) все катушки индуктивности заземлены, поэтому они могут быть непосредственно реализованы макроэлементами на основе конверторов сопротивления (см. рис. 2.4), если в качестве элементов 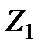 ,
, 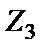 ,
, 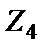 и
и 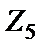 использовать резисторы, а в качестве элемента
использовать резисторы, а в качестве элемента 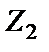 – конденсатор. В этом случае выражение проводимости в узле 1 схемы рис. 2.4 согласно (2.9) имеет вид
– конденсатор. В этом случае выражение проводимости в узле 1 схемы рис. 2.4 согласно (2.9) имеет вид
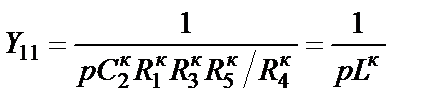 .
.
После замены катушек индуктивности их активными RC-моделями схема конверторного фильтра верхних частот примет вид, показанный на рис. 2.8. Проведя поэлементное сравнение схем рис. 2.8 и рис. 2.2,б, можно получить расчетные соотношения для элементов конверторного ФВЧ на основе данных LC-ФВЧ типа В:
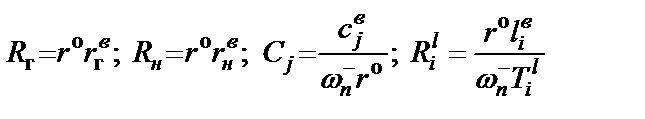 , (2.12)
, (2.12)
где 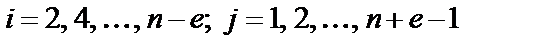 ;
; 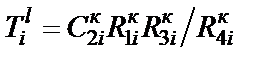 – параметр i-го конвертора, а
– параметр i-го конвертора, а 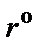 – денормирующее сопротивление, которым необходимо задаться.
– денормирующее сопротивление, которым необходимо задаться.
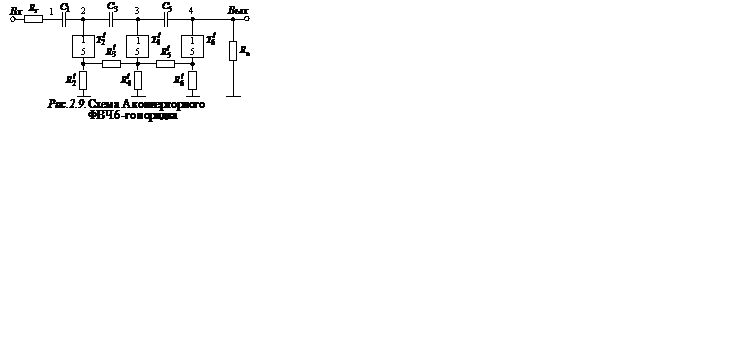 В схеме А конверторного ФВЧ (рис. 2.9) конверторы
В схеме А конверторного ФВЧ (рис. 2.9) конверторы 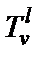 используются для имитации как заземленных, так и незаземленных катушек индуктивности схемы рис. 2.2,а. Чтобы получить расчетные соотношения для схемы рис. 2.9, необходимо в выражениях проводимости элементов схемы рис. 2.2,а перейти от s к p и ввести денормирующее сопротивление
используются для имитации как заземленных, так и незаземленных катушек индуктивности схемы рис. 2.2,а. Чтобы получить расчетные соотношения для схемы рис. 2.9, необходимо в выражениях проводимости элементов схемы рис. 2.2,а перейти от s к p и ввести денормирующее сопротивление 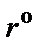 . Поскольку в имитации каждой незаземленной индуктивности используется два конвертора сопротивления, параметры
. Поскольку в имитации каждой незаземленной индуктивности используется два конвертора сопротивления, параметры 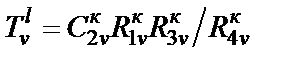 всех конверторов должны быть одинаковыми (
всех конверторов должны быть одинаковыми ( 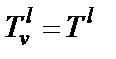 ). В этом случае параметры элементов схемы рис. 2.9 будут описываться следующими соотношениями:
). В этом случае параметры элементов схемы рис. 2.9 будут описываться следующими соотношениями:
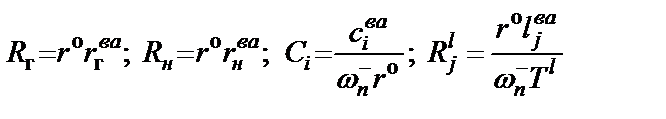 , (2.13)
, (2.13)
где 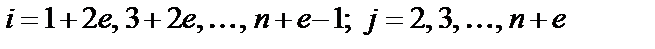 .
.
Параметры элементов схем рис. 2.6, 2.8 и 2.9 могут быть выражены и через параметры элементов схемы рис. 2.1,б, если воспользоваться соотношениями (2.5) и (2.6).
2.3. Полосовые конверторные фильтры
Чтобы конверторная модель полосового лестничного LC-фильтра (см. рис. 2.3) не содержала избыточное число реактивных элементов (конденсаторов), все строки матрицы (2.8), за исключением 0-й строки у фильтров нечеткого порядка, умножаются на оператор 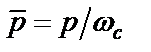 , в результате чего схемы полосовых конверторных фильтров четного (6-го) и нечетного (5-го) порядков примут вид, показанный на рис. 2.10,а и б. В этих схемах
, в результате чего схемы полосовых конверторных фильтров четного (6-го) и нечетного (5-го) порядков примут вид, показанный на рис. 2.10,а и б. В этих схемах 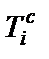 – i-й конвертор сопротивления с двумя конденсаторами
– i-й конвертор сопротивления с двумя конденсаторами 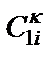 и
и 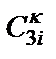 (
(  );
); 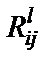 – резисторы, имитирующие соответствующие катушки индуктивности схемы рис. 2.3;
– резисторы, имитирующие соответствующие катушки индуктивности схемы рис. 2.3; 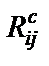 – резисторы, которые совместно с i-м и j-м конверторами имитируют соответствующие конденсаторы схемы LC-фильтра (заземленный конденсатор
– резисторы, которые совместно с i-м и j-м конверторами имитируют соответствующие конденсаторы схемы LC-фильтра (заземленный конденсатор 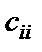 реализуется одним конвертором
реализуется одним конвертором 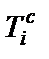 совместно с резистором
совместно с резистором 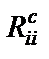 );
); 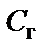 и
и 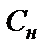 – это преобразованные
– это преобразованные 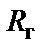 и
и 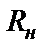 . В схеме фильтра четного порядка (рис. 2.10,а) входная суперемкость
. В схеме фильтра четного порядка (рис. 2.10,а) входная суперемкость 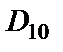 (емкость
(емкость 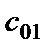 LC-фильтра) реализуется конвертором
LC-фильтра) реализуется конвертором 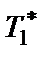 совместно с конденсатором
совместно с конденсатором 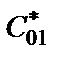 . Конвертор
. Конвертор 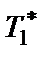 , в отличие от
, в отличие от 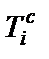 , содержит один конденсатор
, содержит один конденсатор 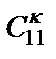 и три резистора
и три резистора 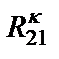 ,
, 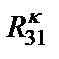 ,
, 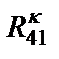 .
.
Составив матрицу проводимостей схемы конверторного фильтра (используя матрицу подсхемы рис. 2.7), путем сопоставления элементов этой матрицы и соответствующей матрицы LC-фильтра можно получить соотношения, связывающие параметры элементов этих схем:
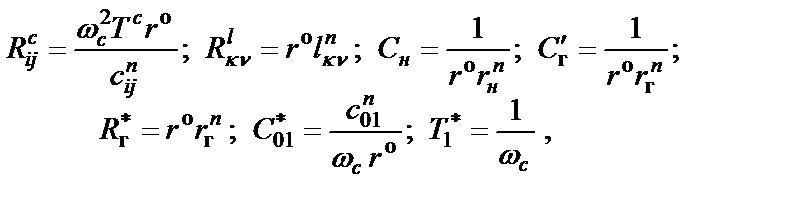 (2.14)
(2.14)
где 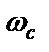 – центральная частота фильтра;
– центральная частота фильтра; 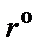 – денормирующее сопротивление;
– денормирующее сопротивление; 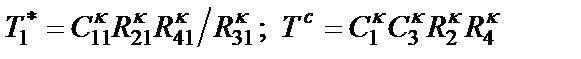 – параметр, одинаковый для всех конверторов
– параметр, одинаковый для всех конверторов 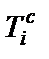 ; параметр
; параметр 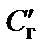 относится только к фильтру нечетного порядка, а параметры, отмеченные «*» в верхнем индексе, – только к фильтру четного порядка;
относится только к фильтру нечетного порядка, а параметры, отмеченные «*» в верхнем индексе, – только к фильтру четного порядка;  и
и 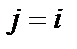 ;
; 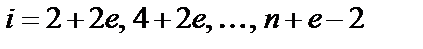 и
и 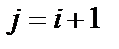 ;
; 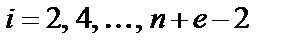 и
и 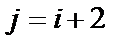 ;
; 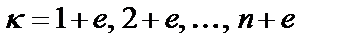 и
и 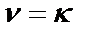 ;
; 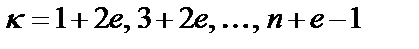 и
и 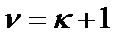 ;
; 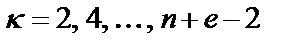 и
и 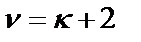 .
.
Рис. 2.10. Полосовые конверторные фильтры:
а – 6-го порядка; б – 5-го порядка
Если полосовой LC-прототип (см. рис. 2.3) оптимизирован по величине коэффициентов динамической перегрузки 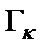 , то и его конверторная модель (рис. 2.10) не будет иметь динамических перегрузок в κ-х (1,2, …) узлах. Однако на выходах операционных усилителей, составляющих конверторы сопротивления,
, то и его конверторная модель (рис. 2.10) не будет иметь динамических перегрузок в κ-х (1,2, …) узлах. Однако на выходах операционных усилителей, составляющих конверторы сопротивления, 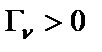 дБ (
дБ ( 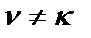 ). Оптимизация
). Оптимизация 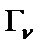 выполняется на этапе расчета схемы конверторного фильтра путем соответствующего выбора параметров элементов конверторов.
выполняется на этапе расчета схемы конверторного фильтра путем соответствующего выбора параметров элементов конверторов.
3. ТЕХНИЧЕСКОЕ ЗАДАНИЕ
C0610с; 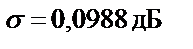
Исходные данные содержатся в таблице 5.13.
Таблица 5.13
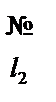
| 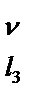
| 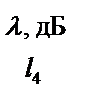
| 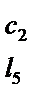
| 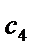
| 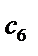
| 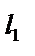
|
| 30 0,0800718 | 2,12408 1,5578596 | 72,73 0,1398629 | 1,3648140 1,3662128 | 1,4828197 | 0,8995567 | 0,8231179 |
Граничная частота полосы пропускания 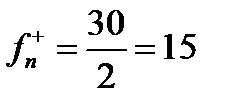 кГц.
кГц.
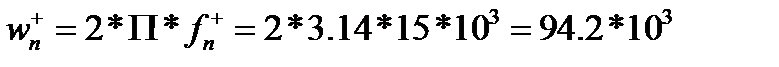 рад/с.
рад/с.
4. СТРУКТУРНАЯ СХЕМА
Руководствуясь (рис. 2.1,а) и соотношениями (2.5), составим схему LC-фильтра 6-го порядка
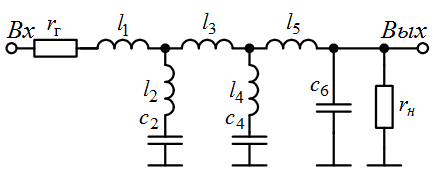
Рис. 2.8.1 Схема лестничного LC- фильтр 6-го порядка
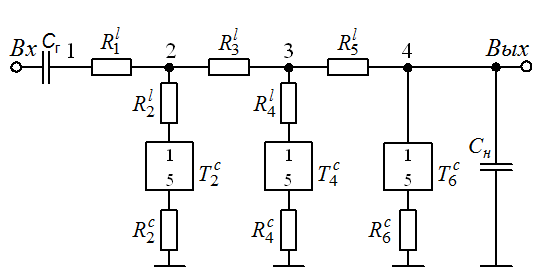
Рис. 2.8.2 Схема конверторного ФВЧ 6-го порядка
5. РАСЧЕТ ЭЛЕМЕНТОВ
Связь между параметрами элементов конверторного ФНЧ-А (рис. 2,б) и параметрами элементов LC-ФНЧ-прототипа (рис. 2,а) описывается базовыми соотношениями (2.11), на основании которых, используя соотношения (2.5), можно выполнить расчет схемы (рис. 2,б) в указанной ниже последовательности.
а) Зададимся денормирующим сопротивлением 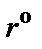 и вычислим
и вычислим
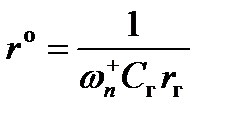 .
.
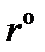 = 52.879 кОм
= 52.879 кОм
При выборе значения 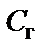 учитываем наличие такого значения в ряду номинальных значений, а также технологические и эксплуатационные ограничения на минимальные и максимальные значения параметров резисторов и конденсаторов. Поскольку для фильтров типа a и c
учитываем наличие такого значения в ряду номинальных значений, а также технологические и эксплуатационные ограничения на минимальные и максимальные значения параметров резисторов и конденсаторов. Поскольку для фильтров типа a и c 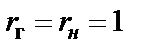 , емкость
, емкость 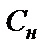 равна емкости
равна емкости 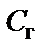 .
.
б) Рассчитаем сопротивления резисторов, имитирующих индуктивности схемы LC-фильтра:
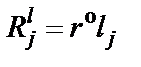 ,
,
где 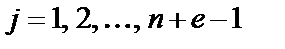 ;
; 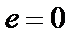 при четном n и
при четном n и 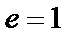 при n нечетном.
при n нечетном.
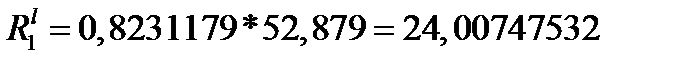 *103
*103
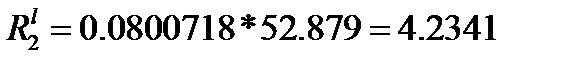 *103
*103
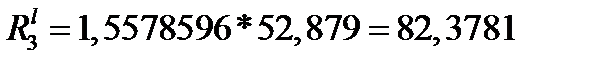 *103
*103
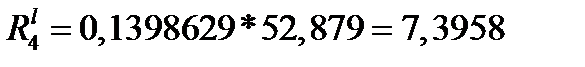 *103
*103
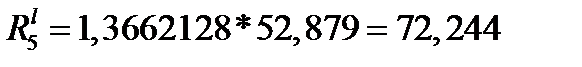 *103
*103








