Практическая работа № 2
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ»
(СГУГиТ)
Институт дистанционного обучения
Кафедра
Космической и физической геодезии
Дисциплина
«Космическая геодезия»
ПРАКТИЧЕСКАЯ РАБОТА №2
Студент: Кусайнгазы М.
Группа: 2Гу
Новосибирск 2019г.
Практическая работа № 2
по курсу “Основы космической геодезии”
для студентов геодезических специальностей 4 курса
Тема: Определение параметров орбиты ИСЗ в начальных условиях движения (задача двух тел)
Цель: усвоить теорию невозмущенного движения небесного объекта и получить практические навыки расчета основных параметров орбиты спутника.
Методические указания к выполнению работы.
1. Титульный лист.
2. Тема и содержание задания.
3. Исходные данные к варианту
Содержание работы:
В момент t0 ракета в точке с координатами
r = (x,y,z)T
сообщила спутнику скорость
r' = (x',y',z')T
(см. варианты задания). Порядок выполнения работы.
1. Получить формулы для вычисления следующих параметров:
а) первых интегралов и константы энергии движения
c = (cx, cy, cz)T ,
б) элементов, задающих размеры, форму орбиты и движение по орбите, к которым относятся:
a - большая полуось, b - малая полуось, e - эксцентриситет, p - фокальный параметр, r- радиус апогея, r - радиус перигея, n - среднее движение, P - период обращения;
в) элементов, задающих ориентировку орбиты, к которым относятся:
i - наклонение, - долгота восходящего узла, w - аргумент перигея;
г) элементов, задающих положение спутника на орбите, к которым относятся:
u -аргумент широты, v - истинная аномалия, M - средняя аномалия, E - эксцентрическая аномалия, t - момент прохождения перицентра.
2. Произвести расчет указанных параметров орбиты по найденным формулам.
3. Выполнить контроль вычислений.
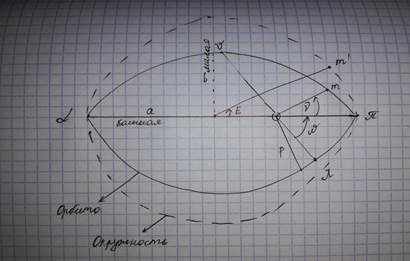
4. Нарисовать два чертежа орбиты с отображением полученных элементов: а) плоский, б) пространственный.
Исходные данные.
| Вариант 23 | ||||||
| = 398600,5 | T0=08h03m 25,69s | |||||
| r, r' | 1644.92 | -6478.07 | 3157.41 | -0.772891 | -2.0577402 | -8.6890011 |
Выполнение работы.
1. Формулы для вычисления параметров орбиты.
а) интеграл Лапласа, интеграл площадей и константа энергии движения:
- модуль вектора положения спутника
r = √(x2 + y2 + z2) r = 7391.91
- модуль вектора скорости спутника
r' = √( x'2 + y'2 + z'2) r' =8.9627
- константа энергии движения
h = r'2 – 2 · /r h =-27.51
- проекции вектора с на оси системы координат Oxyz
cx = y · z' – z · y' cx = 62785.05
cy = z · x' – x · z' cy = 11852.73
cz = x · y' – y · x' cz = -8391.0
- модуль вектора с
с = √(с x 2 + сy 2 + сz 2) с =64442.67
- проекции вектора Лапласа * на оси системы координат Oxyz
движение орбита искусственный спутник
l x = m (/r)·x + cz·y' – сy·z' * x =31554.25
l y = m (/r)·y + cx·z' – сz·x' * y =-202701.31
l z= m (/r)·z + cy·x' – сx·y' * z =-50224.00
- модуль вектора Лапласа
l = √(l x 2 + l y 2 + l z 2) =211201.13
б) элементы, задающие размеры, форму орбиты и движение по орбите:
- эксцентриситет орбиты
e = l / m=0.5298566
- фокальный параметр орбиты
p = c2/ p =17350.137
- большая полуось
a = p/(1 – e2) a =14485.31
- малая полуось
b = a√(1 – e2) b = 11284.87
- расстояние до перицентра
r = a(1 – e) r =6810.17
- расстояние до апоцентра
ra = a(1 + e) ra =22160.16
- среднее движение спутника
n = √(/a3) · 180/ n =0,0207488623
- период обращения спутника
P = 360/n
P =17350.13
в) элементы, задающие ориентировку орбиты:
- наклонение орбиты
i = arccos(cz/c) i =97°17'7".48
- долгота восходящего узла
W= arctg(cx/-cy) =100°24'45".50
- аргумент перицентра
w = arctg [c·* z/(cx·* y - cy·*x)] w =193°31'25".68
г) элементы, задающие положение спутника на орбите:
- аргумент широты спутника
u = arctg[z·c/(y·cx – x·cy)] u =154°17'6".36
- истинная аномалия
v = arctg[c·r·r'/(x·* x + y·* y + z·*z)] v= 320°21'39".96
- эксцентрическая аномалия
tg(E/2) =√[(1 - e)/(1 + e)] · tg(v/2) E =337°19'31".44
- средняя аномалия спутника
M = E – (e·sinE) ·180/ M =349°04'59".52
- время полета спутника от перицентра до его положения на орбите в момент t0
∆t = M/n .t =04°40'24".21
t = t0 - ∆t = 03°23'1".48
2. Контроль вычислений
c · r = 0 c · r =0,000000
c · r' = 0 c · r' =0,000000
c · l^2= 0 c · l=0,000000
3. Графическое отображение полученных элементов
u