Кривые второго порядка
Кривые второго порядка делятся на вырожденные и невырожденные. Вырожденные кривые второго порядка это прямые и точки, которые задаются уравнением второй степени. Если уравнению второго порядка не удовлетворяет ни одна точка плоскости, то тоже говорят, что уравнение определяет вырожденную кривую (мнимую кривую второго порядка).
Классификация линий второго порядка: с помощью специального комплекса действий любое уравнение линии второго порядка приводится к одному из следующих видов:
1) 
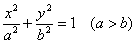– каноническое уравнение эллипса;
2) 
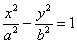– каноническое уравнение гиперболы;
3) 
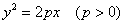– каноническое уравнение параболы;
4) 
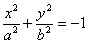– мнимый эллипс;
5) 
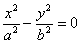– пара пересекающихся прямых;
6) 
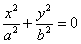– пара мнимых пересекающихся прямых (с единственной действительной точкой пересечения в начале координат);
7) 
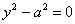– пара параллельных прямых;
8) 
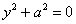– пара мнимых параллельных прямых;
9) 
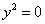– пара совпавших прямых.
Таким образом, существует девять и только девять различных видов линий 2-го порядка, но на практике наиболее часто встречаются эллипс, гипербола и парабола.
1. Эллипс
Эллипсом называется геометрическое место точек плоскости, сумма расстояний от которых до двух фиксированных точек плоскости F1 и F2 есть величина постоянная и равная 2a (2a > |F1F2|). Точки F1 и F2 называют фокусами эллипса. Уравнение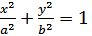 
называется каноническим уравнением эллипса. Система координат, в которой эллипс имеет такое уравнение, называется его канонической системой координат.
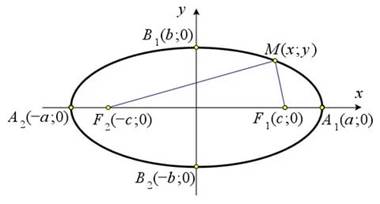
Точки A1, A2, B1, B2 называются вершинами эллипса.
Отрезок A1A2 и его длина 2a называются большой (фокальной) осью, отрезок B1B2 и его длина 2b – малой осью.
Величины a и b называются большой и малой полуосью соответственно.
Длина отрезка F1F2 (равная 2c) называется фокусным расстоянием.
Если M – произвольная точка эллипса, то отрезки MF1, MF2 и их длины r1, r2 называются фокальными радиусами точки M.
Величина ε, равная отношению фокусного расстояния эллипса к его большой оси, называется эксцентриситетом эллипса, т.е.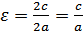 
. Величина ε характеризует форму эллипса.
2. Гипербола
Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от которых до двух фиксированных точек плоскости F1 и F2 есть величина постоянная и равная 2a (2a < |F1F2|). Точки F1 и F2 называют фокусами гиперболы.
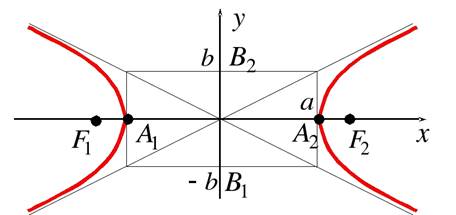Уравнение 
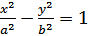называется каноническим уравнением гиперболы. Система координат, в которой эллипс имеет такое уравнение, называется его канонической системой координат.
Точки A1, A2, B1, B2 называются вершинами гиперболы.
Отрезок A1A2 и его длина 2a называются действительной (фокальной) осью, отрезок B1B2 и его длина 2b – мнимой осью.
Величины a и b называются действительной и мнимой полуосью соответственно.
Длина отрезка F1F2 (равная 2c) называется фокусным расстоянием.
Если M – произвольная точка гиперболы, то отрезки MF1, MF2 и их длины r1, r2 называются фокальными радиусами точки M.
Величина ε, равная отношению фокусного расстояния гиперболы к ее действительной оси, называется эксцентриситетом гиперболы, т.е. 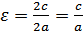. Величина ε характеризует форму гиперболы.
3. Парабола
Параболой называется геометрическое место точек плоскости, расстояние от которых до фиксированной прямой ℓ и до фиксированной точки F (не лежащей на прямой ℓ) одинаково. Точку F называют фокусом параболы, прямую ℓ – директрисой.
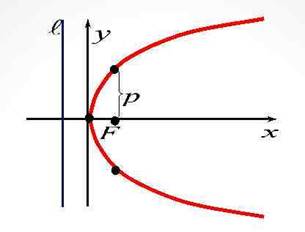Уравнение 
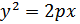называется каноническим уравнением параболы. Система координат, в которой парабола имеет такое уравнение, называется его канонической системой координат.
Точка, в которой парабола пересекает свою ось, называется вершиной параболы
Число p называется параметром параболы.
Если M – произвольная точка параболы, то отрезок MF и его длина называются фокальными радиусами точки M.
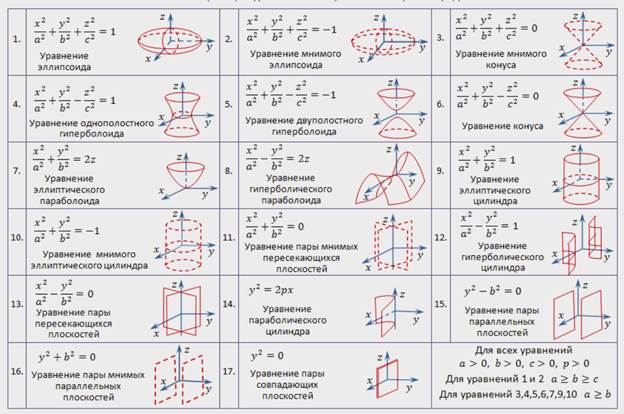
Поверхности второго порядка
