Волновое уравнение.
Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Чтобы получить волновое уравнение, воспользуемся для простоты уравнением плоской волны, распространяющейся вдоль оси x:
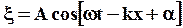
и найдем 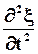 и
и 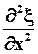 :
:
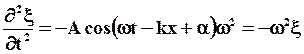 (58)
(58)
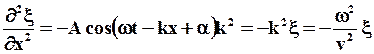 (59)
(59)
Из сравнения (58) и (59) получим волновое уравнение:
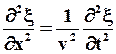 (60)
(60)
Если волна распространяется в произвольном направлении, то волновое уравнение примет вид:
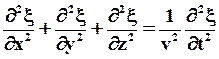 (61)
(61)
Групповая скорость.
Совокупность волн, мало отличающихся друг от друга по частоте, называется волновым пакетом или группой волн. Точка, в которой амплитуда колебаний группы волн максимальна, называется центром группы волн. Скорость, с которой распространяется максимум колебательного процесса (скорость центра группы волн), называется групповой скоростью. Групповая скорость – скорость передачи энергии группой волн.
В зависимости от частоты колебаний может меняться и скорость распространения волны. Зависимость скорости распространения волны от частоты колебаний частиц среды называется дисперсией.
Волновое число k равно:
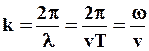
Дисперсия приводит к нарушению линейной зависимости между k и w. Зависимость w = w ( k ) называется дисперсионным уравнением или законом дисперсии.
Если среда не обладает дисперсией, то все гармонические волны независимо от частоты распространяются с одной и той же фазовой скоростью и пакет ведет себя как стационарная волна, т.е. 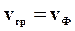 , если в среде имеет место дисперсия, то
, если в среде имеет место дисперсия, то 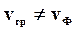 .
.
Найдем связь между групповой и фазовой скоростями. Преобразуем выражение для фазы волны (51):
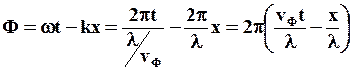 (62)
(62)
Для сохранения пакета волн необходимо, чтобы в центре пакета находился набор когерентных волн, распространяющихся с одинаковыми скоростями. Для таких волн изменение фазы в зависимости от длины волны должно быть равно нулю:
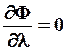 (63)
(63)
Взяв производную по l от (62) и приравняв ее к нулю, после несложных преобразований получим:
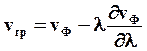 (64)
(64)
Если 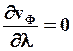 , то
, то 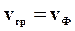 - дисперсия отсутствует.
- дисперсия отсутствует.
Если 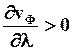 , то
, то 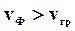 - в среде имеет место нормальная дисперсия.
- в среде имеет место нормальная дисперсия.
Если 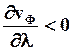 , то
, то 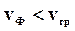 - в среде аномальная дисперсия.
- в среде аномальная дисперсия.
Энергия упругой волны. Плотность энергии.
Пусть в среде вдоль оси x распространяется плоская волна:
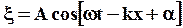
Выделим малый объем D V среды, масса которого M = r D V, где r - плотность среды.
Все точки этой среды совершают колебания со скоростью u:
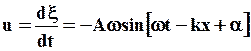
Кинетическая энергия частицы 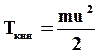 , кинетическая энергия всех частиц среды в объеме D V
, кинетическая энергия всех частиц среды в объеме D V
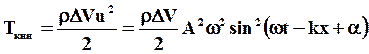 (65)
(65)
Кинетическая энергия выделенного объема меняется с течением времени, поэтому найдем среднее значение ее за период 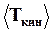 . Т.к. среднее за период значение квадрата синуса равно 1/2, то
. Т.к. среднее за период значение квадрата синуса равно 1/2, то
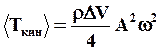 (66)
(66)
Частицы среды, совершающие колебательное движение, обладают не только кинетической, но и потенциальной энергией U. Ранее было показано, что средние за период значения кинетической и потенциальной энергии ГО одинаковы. Аналогично, в случае среды, в которой распространяется волна:
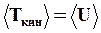 (67)
(67)
Тогда среднее значение за период энергии среды в объеме D V при распространении в ней волны будет равно:
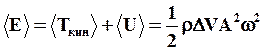 (68)
(68)
Энергия упругой волны, заключенная в единице объема называется объемной плотностью энергии волны.
Разделив (24) на DV, получим среднюю за период объемную плотность энергии волны:
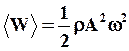 (69)
(69)
Поток энергии. Плотность потока энергии.
Волна, распространяясь в среде, переносит энергию. Для характеристики переноса энергии волнами вводится понятие потока энергии.
Потоком энергии называется количество энергии, переносимое волной через некоторую поверхность за единицу времени:
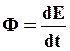 (70)
(70)
Пусть dE – энергия, перенесенная за время dt через площадку S 1, перпендикулярную к направлению распространения волны.
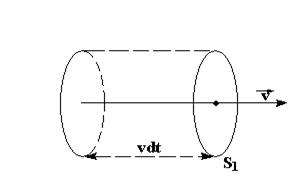
| Очевидно, за время dt через S 1 будет перенесена вся энергия, заключенная в цилиндрическом слое длиной vdt, где v – скорость распространения волны. Если W – объемная плотность энергии, то
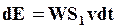 и и 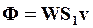 (71) (71)
|
В общем случае поверхность S может быть неплоской и не перпендикулярной направлению распространения волны. Поэтому вводят понятие плотности потокам энергии.
Количество энергии, переносимое волнами за единицу времени через единичную площадку, нормальную к направлению распространения волны, называется плотностью потока энергии
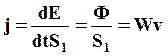 (72)
(72)
Т.к. скорость 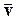 является вектором, то и плотность потока энергии принято считать векторной величиной:
является вектором, то и плотность потока энергии принято считать векторной величиной:
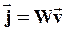 (73)
(73)
Этот вектор называется вектором Умова.
Среднее за период значение 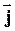 равно
равно
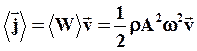 (74)
(74)
Среднее по времени значение плотности потока энергии называют интенсивностью волны в данной точке.








