Плоские, сферические и цилиндрические волны.
Распространяясь от источника колебаний, волна захватывает все новые и новые области пространства.
Геометрическое место точек, до которых доходят колебания к моменту времени t, называется фронтом волны.
Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью.
По форме волновой поверхности различают плоские, сферические и цилиндрические волны. В случае плоской волны волновые поверхности представляют собой множество параллельных друг другу плоскостей, в случае сферической волны – множество концентрических сфер, в случае цилиндрической – систему соосных цилиндрических поверхностей.
Уравнение плоской волны.
Уравнением волны называется выражение, которое определяет смещение колеблющейся частицы как функцию координат и времени:
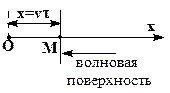
|  Пусть плоская волна распространяется вдоль оси x, а точка O является источником колебаний и колеблется по закону:
Пусть плоская волна распространяется вдоль оси x, а точка O является источником колебаний и колеблется по закону:
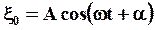 (48) (48)
|
t – время, отсчитанное от начала колебаний т. O .
Выберем на прямой, вдоль которой распространяется волна, произвольную точку M на расстоянии x от источника колебаний. Колебания дойдут до точки M через промежуток времени 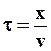 , где v – скорость распространения волны.
, где v – скорость распространения волны.
Точка M начнет колебаться позже т. O, но с той же амплитудой A и частотой w. Тогда смещение точки M из положения равновесия запишется в виде:
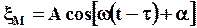 (49)
(49)
Для любой точки:
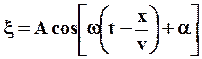 (50)
(50)
Это уравнение позволяет определить смещение из положения равновесия любой точки волны и называется уравнением плоской волны, распространяющейся вдоль оси x .
Аргумент тригонометрической функции называется фазой волны:
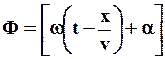 (51)
(51)
Преобразуем это выражение, для чего введем понятие длины волны.
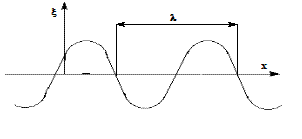
| Изобразим моментальный снимок волны, т.е. график зависимости 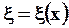 для фиксированного момента времени t. для фиксированного момента времени t.
|
Расстояние между ближайшими точками, колеблющимися в одинаковой фазе, называется длиной волны. Длину волны можно определить так же, как расстояние, пройденное волной за период колебаний частиц среды:
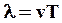 (52)
(52)
Преобразуем (51) с учетом (52)
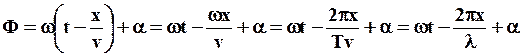 (53)
(53)
Тогда уравнение волны, распространяющейся вдоль оси x, запишется в виде:
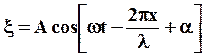 (54)
(54)
Введем величину:
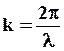 (55)
(55)
которая называется волновым числом, и придем к следующему уравнению плоской волны, распространяющейся вдоль оси x:
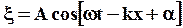 (56)
(56)
Разность фаз:
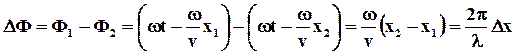
Фазовая скорость.
Рассмотрим некоторую волновую поверхность, например, плоскость, содержащую т.M. Очевидно, фаза волны 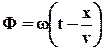 в этой плоскости будет меняться с течением времени. Чтобы фаза оставалась постоянной, плоскость должна перемещаться с некоторой скоростью
в этой плоскости будет меняться с течением времени. Чтобы фаза оставалась постоянной, плоскость должна перемещаться с некоторой скоростью 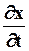 вдоль оси x.
вдоль оси x.
Скорость перемещения определенной фазы волны называется фазовой скоростью 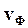 .
.
Найдем фазовую скорость из условия, что
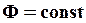 и
и 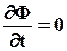 :
:
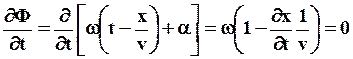
откуда: 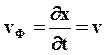 (57)
(57)
Фазовая скорость равна скорости распространения волны.








