Вынужденные колебания осциллятора под действием синусоидальной силы.
Колебания, которые совершаются за счет работы внешних сил, называются вынужденными, а действующая сила – вынуждающей.
Рассмотрим простейший случай – воздействие на систему внешней силы, меняющейся по гармоническому закону:
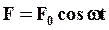 (40)
(40)
где 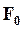 и
и 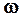 - соответственно амплитудное значение и частота вынуждающей силы.
- соответственно амплитудное значение и частота вынуждающей силы.
Запишем II закон Ньютона для вынужденных колебаний:
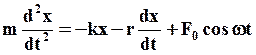 (41)
(41)
и вводя обозначения 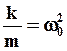 и
и 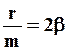 , получим дифференциальное уравнение вынужденных колебаний ГО:
, получим дифференциальное уравнение вынужденных колебаний ГО:
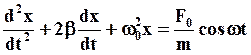 (42)
(42)
Сразу после приложения вынуждающей силы возникает переходный режим вынужденных колебаний, при котором система участвует в двух колебаниях – свободных затухающих колебаниях и незатухающих колебаниях с частотой w вынуждающей силы. Однако через некоторое время t свободные колебания системы практически прекращаются. Система переходит в состояние установившихся вынужденных колебаний, которые происходят по тому же закону и с той же частотой, с которой меняется вынуждающая сила.
Поэтому естественно предположить, что решение (42) должно иметь вид:
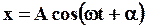 (43)
(43)
Неизвестные амплитуду и начальную фазу найдем с помощью векторной диаграммы этого колебания.
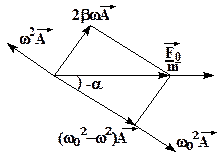
| Построим векторную диаграмму для начального момента времени t 0. Функция 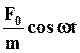 изобразится вектором изобразится вектором 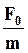 , направленным по оси Ox. Функция , направленным по оси Ox. Функция
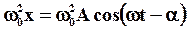
|
изобразится вектором 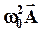 длиной
длиной 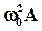 , отложенным от оси Ox под углом (-a). Ускорение
, отложенным от оси Ox под углом (-a). Ускорение 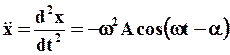 изобразится вектором
изобразится вектором 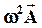 длиной
длиной 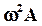 , направленным противоположно вектору
, направленным противоположно вектору 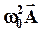 . Наконец, функция
. Наконец, функция
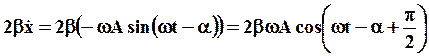
изобразится вектором длиной 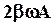 , перпендикулярным
, перпендикулярным 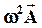 , из треугольника видно, что
, из треугольника видно, что
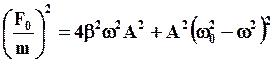
Следовательно, амплитуда установившихся вынужденных колебаний равна:
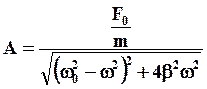 (44)
(44)
а начальная фаза определяется из соотношения:
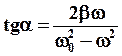 (45)
(45)
Резонансные кривые
Из (44) следует, что амплитуда A вынужденных колебаний зависит от частоты 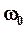 собственных колебаний, от частоты
собственных колебаний, от частоты 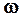 , амплитуды
, амплитуды 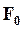 вынуждающей силы и коэффициента затухания
вынуждающей силы и коэффициента затухания 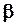 .
.
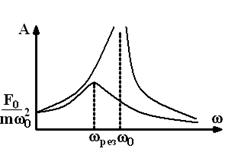
| На рис. представлен график зависимости амплитуды A вынужденных колебаний от частоты  и вынуждающей силы.
1. Пусть и вынуждающей силы.
1. Пусть 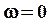 , тогда , тогда 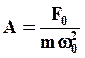 .
2. Пусть .
2. Пусть 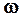 возрастает и стремится к возрастает и стремится к 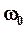 . Если . Если 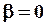 , то с ростом , то с ростом 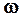 растет амплитуда A и при растет амплитуда A и при 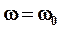 A обращается в бесконечность. A обращается в бесконечность.
|
В реальных условиях 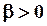 , поэтому при
, поэтому при 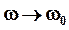 амплитуда растет не до бесконечности, а до некоторого максимального значения Amax .
амплитуда растет не до бесконечности, а до некоторого максимального значения Amax .
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте собственных колебаний называется резонансом.
Частота 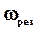 , при которой A = Amax, называется резонансной частотой.
, при которой A = Amax, называется резонансной частотой.
3. При дальнейшем возрастании 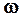 (
( 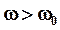 ) амплитуда A уменьшается.
) амплитуда A уменьшается.
Найдем резонансную частоту 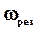 из условия минимума подкоренного выражения (44). Для этого возьмем производную по
из условия минимума подкоренного выражения (44). Для этого возьмем производную по 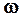 и приравняем к нулю..
и приравняем к нулю..
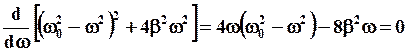
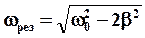 ,
,
откуда видно, что при 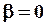
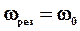 , при
, при 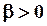
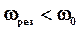 .
.
Найдем сдвиг фаз при резонансе:
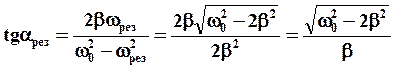
Если 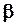 мало, то
мало, то 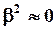 и
и 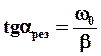 . Если
. Если 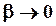 , то
, то 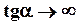 и
и 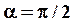 , т.е. смещение при вынужденных колебаниях отстает по фазе от вынуждающей силы на
, т.е. смещение при вынужденных колебаниях отстает по фазе от вынуждающей силы на 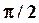
Волновые процессы.








