Графическое представление колебаний. Векторная диаграмма.
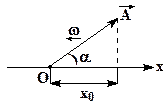
| Выберем некоторую ось Ox и из точки O построим вектор 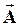 , длиной A, образующий с осью Ox угол a. Проекция этого вектора на ось Ox в начальный момент времени t 0 =0 равна: , длиной A, образующий с осью Ox угол a. Проекция этого вектора на ось Ox в начальный момент времени t 0 =0 равна:
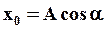
|
Будем вращать этот вектор с угловой скоростью 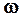 . За время
. За время 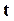 вектор
вектор 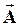 повернется на угол
повернется на угол 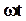 , и его проекция на ось Ox в этот момент будет:
, и его проекция на ось Ox в этот момент будет:
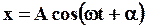
При вращении 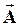 его проекция будет меняться в пределах от A до –A. За то время, пока
его проекция будет меняться в пределах от A до –A. За то время, пока 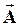 повернется на угол
повернется на угол 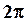 , его проекция совершит одно полное колебание, причем координата этой проекции будет меняться по закону
, его проекция совершит одно полное колебание, причем координата этой проекции будет меняться по закону 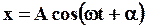
Таким образом, гармоническое колебание может быть представлено с помощью вектора, длина которого равна амплитуде колебания, отложенного из произвольной точки под углом, равным начальной фазе, и вращающегося с угловой скоростью 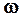 вокруг этой точки.
вокруг этой точки.
Собственные колебания гармонического осциллятора.
Рассмотри колебания частицы под действием упругой или квазиупругой силы 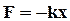 . Коэффициент
. Коэффициент 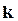 называется коэффициентом упругости. По второму закону Ньютона:
называется коэффициентом упругости. По второму закону Ньютона:
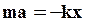
или 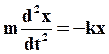 (5)
(5)
Разделим (5) почленно на массу частицы 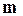 и обозначим:
и обозначим:
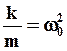 (6)
(6)
Тогда уравнение (5) примет вид:
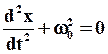 (7)
(7)
Решением дифференциального уравнения (7) являются функции:
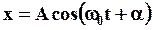 или
или
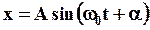 (8)
(8)
Таким образом, система, находящаяся под действием силы вида 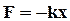 , совершает гармоническое колебание. Частота этого колебания:
, совершает гармоническое колебание. Частота этого колебания:
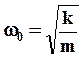 (9)
(9)
период колебания:
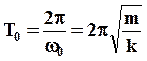 (10)
(10)
Энергия гармонических колебаний.
Пусть гармонический осциллятор (ГО) колеблется по закону:
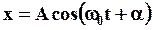
Полная энергия колебаний ГО равна:
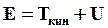 (11)
(11)
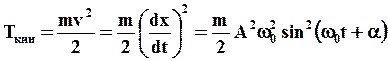 (12)
(12)
Потенциальная энергия осциллятора:
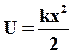 (13)
(13)
Получаем (с учетом 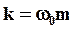 ):
):
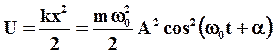 (14)
(14)
Тогда:
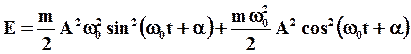
или:
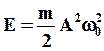 (15)
(15)
Т.о., полная энергия гармонического колебания пропорциональна квадрату амплитуды и постоянна во все время колебания, как это следует из закона сохранения механической энергии. При этом кинетическая и потенциальная энергия непрерывно меняются с течением времени, переходя друг в друга.
Средние за период значения кинетической и потенциальной энергии одинаковы и равны:
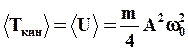 (16)
(16)
т.к. средние за период значения квадрата синуса и квадрата косинуса равны 1/2.
Физический маятник.
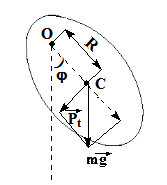
Физическим маятником называют всякое абсолютно твердое тело, способное вращаться вокруг неподвижной оси, не проходящей через центр тяжести. Колебания физического маятника происходят под действием составляющей 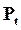 силы тяжести
силы тяжести 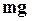 .
.
| 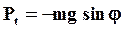 Знак «-» берется потому, что сила
Знак «-» берется потому, что сила 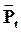 стремится вернуть маятник в положение равновесия. Сила стремится вернуть маятник в положение равновесия. Сила 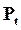 будет квазиупругой, т.е. пропорциональной смещению, только при малых углах отклонения будет квазиупругой, т.е. пропорциональной смещению, только при малых углах отклонения 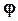 , когда , когда 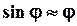 и и
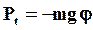 (17) (17)
|
Эта сила создает вращающий момент 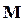 относительно оси вращения, проходящей через точку подвеса O перпендикулярно плоскости чертежа, равный:
относительно оси вращения, проходящей через точку подвеса O перпендикулярно плоскости чертежа, равный:
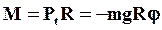 (18)
(18)
R – расстояние от точки подвеса до центра тяжести C маятника.
Запишем уравнение вращательного движения относительно оси вращения:
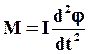 или
или 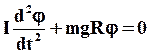 (19)
(19)
где I – момент инерции маятника относительно оси вращения
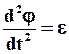 - угловое ускорение.
- угловое ускорение.
Разделив (19) на I, получим дифференциальное уравнение малых колебаний физического маятника:
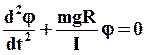 (20)
(20)
Из него следует, что частота колебаний физического маятника:
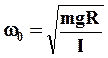 (21)
(21)
а период колебаний:
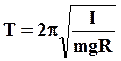 (22)
(22)
Приведенной длиной 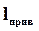 физического маятника называется длина такого математического маятника, который колеблется синхронно с физическим. Из условия синхронности
физического маятника называется длина такого математического маятника, который колеблется синхронно с физическим. Из условия синхронности 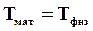 , где
, где 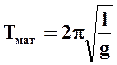 , найдем, что
, найдем, что 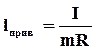 .
.








