Приклади завдань PISA (математика)
Група завдань: ВИГЛЯД БАШТИ
На малюнку зображено вигляд даху башти зверху. Крім того, знаком ( 
) показано п'ять різних позицій спостерігача, позначених P1 – P5.
З кожною з цих позицій спостерігач може бачити декілька граней даху башти.
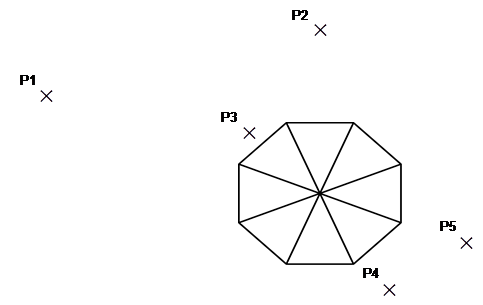
У таблиці обведіть кількість граней, які можна бачити з кожної із зазначених позицій.
| Позиція | Кількість граней, які можна бачити с наданої позиції |
| P1 | 1 2 3 4 більш, ніж 4 |
| P2 | 1 2 3 4 більш, ніж 4 |
| P3 | 1 2 3 4 більш, ніж 4 |
| P4 | 1 2 3 4 більш, ніж 4 |
| P5 | 1 2 3 4 більш, ніж 4 |
У даному випадку потрібно визначити кути, що обмежують кількість видимих граней даху вежі з кожної позначеної позиції спостереження. Для цього потрібно продовжити бічні сторони трикутників, на які розділений восьмикутник (становить собою вигляд зверху 8 граней даху вежі), а також провести дотичні з кожної позиції. Утворюються кути, усередину яких потрапляє кожна з 5 позицій, що відповідає розташуванню спостерігача.
Група завдань – ДВЕРІ, що ОБЕРТАЮТЬСЯ
Двері мають три скляні перегородки, що разом з цими дверима обертаються усередині кругового простору. Внутрішній діаметр цього простору 2 метри (200 сантиметрів). Три дверні перегородки ділять простір на три рівні сектори. Нижче на плані показані дверні перегородки в трьох різних позиціях, якщо дивитися на них зверху.
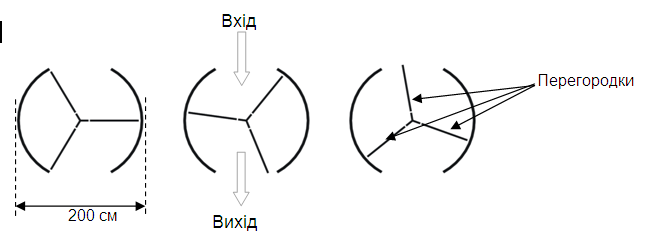
Запитання 1:
Чому дорівнює в градусах кут між двома дверними перегородками?
Для відповіді на питання потрібно обчислити градусну міру центрального кута.
|
Запитання 2:
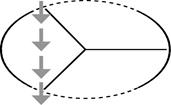Два дверні отвори (пунктирні дуги на рисунку) мають однаковий розмір. Якщо вони дуже широкі, то двері, що обертаються, не зможуть заслонити відчинений простір, і повітря вільно поступатиме через вхід і вихід. Це призведе або до втрати тепла, або до його збільшення. Зазначений випадок показаний на рисунку справа.
Яку найбільшу довжину дуги в сантиметрах (см) може мати кожен дверний отвір, щоб повітря ніколи не змогло вільно поступати через вхід і вихід?