Российской Федерации федеральное государственное
МИНИСТЕРСТВО НАУКИ ВЫСШЕГО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ
БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ОБРАЗОВАНИЯ «ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ
УНИВЕРСИТЕТ»
МНОГОПРОФИЛЬНЫЙ КОЛЛЕДЖ
Нефтегазовое отделение Ю. Г. Эрвье
Исследовательская работа
На тему
«Параболы в арочных мостах»
Выполнил:
Боярских А. А.
Обучающийся группы Орср 20-(9)-1
Руководитель: Баймагамбетова Л. Ю.
Преподаватель ОИД
Тюмень, 2021
Содержание
I. Введение ………………………………………………………........3
II. Основная часть …………………………………………………....4
2.1 Теоретическая часть ………………………………………….......4
2.1.1 Параболы ……………………………………………………….4
2.1.2 Параболы в колокольчике ……………………………………... 5
2.1.3 Из истории мостостроения в России с XII по XIX века .......5-8
2.1.4 Виды мостов …………………………………………………...8-9
2.1.5 Арочные мосты …………………………………………….9-10
2.2 Практическая часть …………………………………………..11-13
III. Заключение ………………………………………………………...14
Библиографический список …………………………………………..15
Приложение ………………………………………………………...16-18
I .Введение
В повседневной жизни довольно часто нам встречаются дугообразные конструкции; эта форма широко распространена не только из-за эстетичного внешнего вида, но из-за способности выдерживать нагрузки, вызываемые весом самого сооружение и дополнительными факторами. К таким сооружениям относятся арки, купола храмов, акведуки, однако в этой работе будут рассмотрены мосты Санкт-Петербурга.
Цель: Изучение материала о свойствах квадратичной функции и исследование
графика- параболы в арочных мостах Санкт-Петербурга.
Для достижения цели были поставлены следующие задачи:
1. Изучить литературу про мосты Санкт-Петербурга;
2. Изучить теорию квадратичной функции и её графика;
3. Найти и сфотографировать арочные мосты в Петербурге;
4. Овладеть методикой задания уравнениями графиков квадратичной функции
и исследовать их свойства.
Гипотеза: Ни одного архитектурного сооружения в нашем мире не существовало бы без предварительных точных расчетов, которые помогает делать наука под названием математика.
Методы исследования:
1. теоретический анализ литературы по теме исследования;
2. наблюдение;
Объект исследования: арочные мосты Санкт-Петербурга
Предмет исследования: свойства параболы, применяемые при строительстве арочных мостов Санкт-Петербурга
II . Основная часть
2.1 Теоретическая часть
2.1.1 Парабола
термин функция (от лат. function – исполнение, совершение) впервые был введен немецким ученым Г. Лейбницем в конце 17 века. Функцией называется зависимость между двумя переменными x и y, при которой каждому значению х соответствует единственное значение у. Одним из способов задания функции является график. Графиком функции называется множество точек в системе координат, абсциссы которых равны аргументу, а ординаты – соответствующим значениям функции. Существует довольно много видов функций: линейная, квадратичная, степенная, показательная, логарифмическая, тригонометрическая и другие, каждая из них задается уравнением и графиком. Линейная функция задается прямой, квадратичная – квадратичной параболой, степенная функции вида у=х2k+1 (где k – натуральное число) - кубической парабола, функция вида y – гиперболой и тд. В данной работе будут рассмотрены исключительно квадратичная функция и ее график. Функция вида y=ax2+bx+c, где a, называется квадратичной. Графиком этой функции является парабола. Парабола – это геометрическое место точек, равноудаленных от данной прямой и данной точки.
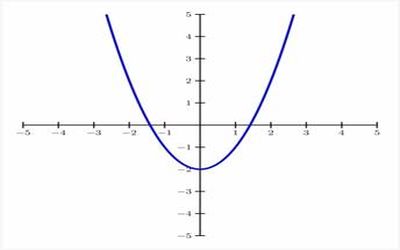
Рис. 1. График квадратичной функции
Чтобы построить график функции вида y=ax2+bx+c, нужно найти координаты вершины графика. Х вершины = (-b)/2a; для нахождения у вершины нужно подставить значение найденного x в данное уравнение; график функции y=ax2+bx+c получается из графика функции у=aх2 сдвигом в точку (х вершины; у вершины).Довольно часто мы сталкиваемся с параболическими формами. Например, во время или после дождя мы наблюдаем радугу. В лепестках некоторых цветов, в очертании горных хребтов и вершин можно разглядеть параболу.
2.1.2 Параболы в колокольчике
Гуляя по городу, мы часто видим дугообразные конструкции. Архитекторы используют параболическую форму в проектировании арок, мостов, куполов, потолков. Во-первых, именно такая форма придает эстетичный вид, во-вторых, параболическим конструкциям присуща прочность, потому что сила, создаваемая нагрузкой на мост или арку, не толкает вниз, а распределяется вдоль дуги, то есть эти строения поддерживают сами себя. В куполах всех храмов и церквей используется этот же принцип. В данной работе будут рассмотрены мосты в Санкт-Петербурге.
Прежде чем рассматривать виды мостов и их преимущества, познакомимся с историей мостостроения в России.
2.1.3 Из истории мостостроения в России с XII по XIX века
Постройка мостов, вероятно, началась очень давно. При Владимире Мономахе в 1115 году был построен наплавной мост через Днепр в Киев, при Дмитрии Донском во время осады Твери были построены 2 моста, а во время войны с татарами в 1380 году возвели мост через Дон. Кроме того, в Новгородской летописи упоминается о «разборчатых» мостах в Новгороде через реку Волхов(рис.4).например, Симеоновский через Фонтанку, оформленный под каменный арочный мост. Остальные мосты через Мойку и Фонтанку построены в период времени 1742-1749гг., т.е. во время правления Елизаветы Петровны. При ней же был возведен Исаакиевский мост(рис.4).

Рис.4. Мост 12 века через реку Волхов
При Екатерине 11 в Петербурге началась замена деревянных мостов на каменные на реке Фонтанке, строение Казанского и Каменного мостов через Екатерининский канал, в Москве через реку Яузу был возведен Дворцовый мост. С началом строительства в 1817 году Петербурго-Московского шоссе появилось множество каменных мостов, пролеты которых могли достигать 9 саж. В 40-х годах строилось несколько каменных мостов в Тифлисе, например, Михайловский мост с пролетом в 15 саж (32м).
Чугунные арочные мосты впервые появились в 1806 году в Петербурге при Александре 1, это были первые металлические мосты в России. Были построены Полицейский, Красный, Синий, Поцелуев, Мало-Семеновский мосты. Цепные мосты введены в Россию в 1822 году по предложению французских инженеров. Распространение таких мостов захватило период с 1824 по 1853 год. К цепным мостам относятся Пантелеймоновский, пешеходные через Екатерининский канал и Мойку, Египетский, проволочный Лиговский через Западный Бур в Брест, мост через Нарву в Ивангород, Киевский через Днепр и Островский через реку Великую. До 1873 года из подвижных мостов с постоянными опорами применялись только подъемные с горизонтальной осью вращения. Поворотные мосты появились в первые при строительстве Николаевского моста в Петербурге и цепного моста в Киеве 1853 году
2.1.4 Виды мостов
I . Балочный мост
Балочные мосты используются для перекрытия небольших пролетов. Отличаются простотой строения и прочностью. Балочные мосты способны выдержать большие вертикальные нагрузки, но не горизонтальные, такие как сильный ветер. Также такие мосты чувствительны к деформации основания. Из-за этих недостатков балочные конструкции почти не используются в современном мостостроении.

Рис.5. Бердов мост
II . Висячий мост
Главное преимущество висячих мостов состоит в том, что основной пролет можно сделать максимально длинным, используя небольшое количество материала. Балочные мосты не требуют дополнительных опор, также их можно строить достаточно высоко, что дает возможность судам проходить под ними. Но под действием сильного ветра опоры крайне неустойчивы, поэтому во время штормов некоторые мосты перекрывают.

Рис.6. Почтамтский
III .Вантовый мост
Это тип висячего моста. Имеет такие же преимущества, но по сравнению с висячим он более устойчив к суровым погодным условиям.

Рис.7. Большой Обуховский мост
2.1.5 Арочные мосты
Арочный мост - мост с пролётными строениями, основными несущим конструкциями которых служат арки.
Основные размеры элементов арочных мостов – высота и ширина балок, толщина плиты, высота и ширина арок, количество арматуры и т.п. – окончательно устанавливаются на основании расчета сооружения в соответствии с действующими на сооружение нагрузками и качеством материалов, из которых строится мост.
Выбор толщины арки затруднителен вследствие большого разнообразия факторов, влияющих на этот выбор, таких как величина нагрузки, марка бетона и т.д. Примерно можно принимать:
d= 145÷150L;
где d – толщина арки, L – расчетный пролет арки.
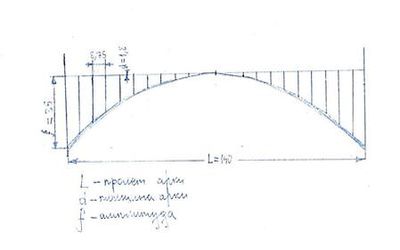
Рис.8. Размеры модели моста
Также для строения моста необходимо рассчитать максимально возможную нагрузку на конструкцию. Для этого используется формула Журавского, которая представлена на рис.9.

Рис.9. Формула Журавского
2.2 Практическая часть
Казанский мост
Казанский мост перекинут через канал Грибоедова, соединяя Казанский и Спасский острова. Длина переправы — 17,35 метров, ширина — 95 метров. Это третий по ширине мост в Петербурге после Синего и Аптекарского мостов. С 1716 года существовал деревянный мост через речку Кривушу. В 1737 году мост получил имя Рождественский, поскольку рядом располагалась церковь Рождества Богородицы. Со второй половины XVIII века Рождественскую церковь стали называть Казанской. Такое же наименование закрепилось и за новым каменным мостом, построенным в 1766 году. В 1805-1806 годах, в связи с постройкой Казанского собора и перепланировкой участка, примыкающего к Невскому проспекту, мост перестроили, предположительно, по проекту архитектора Л.И. Руска. Мост расширили до 95 м, а его длина составила 17,5м. На фотографии Казанского представлены система координат и график квадратичной функции. Чтобы задать уравнение, мною был введен единичный отрезок.
y=ax²+bx+c








