Коэффициент готовности K – вероятность того, что элемент работоспособен в произвольный момент времени.
Для определения величины K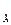 
отдельного элемента используется следующая статистическая оценка:
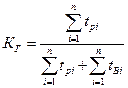, (4.12)
где t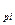 
– i-й интервал времени исправной работы элемента, t 
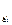– i-й интервал времени восстановления элемента после i-го отказа, n – число отказов.
Разделив численно знаменатель выражения (4.12) на число отказов n, происшедших за рассматриваемое время, получим следующее выражение:
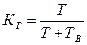. (4.13)
Таким образом, коэффициент готовности равен вероятности пребывания элемента в работоспособном состоянии в произвольный момент времени в рассматриваемом периоде.
Коэффициент готовности имеет смысл надежностного коэффициента полезного действия, так как числитель представляет собой полезную составляющую, а знаменатель – общие затраты времени.
Коэффициент готовности является важным показателем надежности, так как характеризует готовность элемента к работе и позволяет также оценить его эксплуатационные качества (удобство эксплуатации, стоимость эксплуатации) и требуемую квалификацию обслуживающего персонала.
Коэффициент простоя Кп – вероятность того, что элемент неработоспособен в любой момент времени.
Статистическая оценка величины Кп:
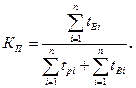(4.14)
По аналогии с коэффициентом готовности получаем зависимость для коэффициента простоя:
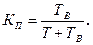(4.15)
Очевидно, что всегда имеет место равенство
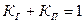. (4.16)
Относительный коэффициент простоя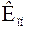 
– отношение коэффициента простоя к коэффициенту готовности:
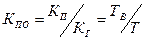. (4.17)
Коэффициент технического использования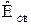 
учитывает дополнительные преднамеренные отключения элемента, необходимые для проведения планово-предупредительных ремонтов:
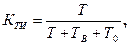(4.18)
где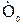 
– среднее время обслуживания, т.е. среднее время нахождения элемента в отключенном состоянии для производства планово-предупредительных ремонтов (профилактики).
Коэффициент оперативной готовности Ког – вероятность того, что элемент работоспособен в произвольный момент времени t и безошибочно проработает в течение заданного времени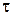 
(t,t+ ):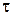
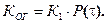(4.19)
Для определения величины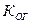 
используется статистическая оценка
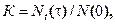(4.20)
где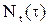 
– число элементов, исправных в момент времени t и безотказно проработавших в течение времени 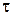, N(0) – первоначальное число наблюдаемых элементов в момент времени t = 0.
Коэффициент оперативной готовности позволяет количественно оценить надежность объекта в аварийных условиях, т.е. до окончания выполнения какой-то эпизодической функции.
Пример 4.1
Проводилось наблюдение за работой элемента на интервале времени t = 1300 ч, в течение которого было зафиксировано N(0)=14 отказов. Требуется определить среднюю наработку на отказ, если известно среднее время восстановления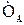 
=2 ч, а вывод элемента из работы для проведения профилактических ремонтов не производился.
Решение
Используем формулу (3.17). С учетом времени восстановления элемента после отказов получаем
T=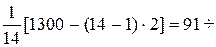 
.
Пример 4.2
Определить коэффициенты готовности, простоя и коэффициент технического использования для трансформатора с высшим напряжением 35, 110 кВ.
Решение
Из табл. 3.2 берем исходные показатели надежности (для резервированной системы):
, 
, 
.
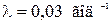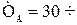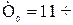Тогда Т =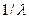 
= 1/0,03 = 33,33 года.
Расчеты по формулам (4.13), (4.16), (4.18) дают следующие результаты:
К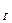 
= 
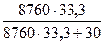=0,999897; К 
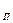=1-0,999897=0,000103;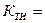 
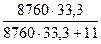=0,999859.
Структурная надёжность
5. О ПРЕДЕЛЕНИЕ НАДЕЖНОСТИ СИСТЕМ ПО ПОКАЗАТЕЛЯМ НАДЕЖНОСТИ ВХОДЯЩИХ В НИХ ЭЛЕМЕНТОВ
Структурной надежностью системы (устройства) называется результирующая надежность системы (устройства) при заданной ее структуре и известных значениях надежности всех входящих в нее частей (элементов).
Надежность систем зависит не только от составляющих их элементов, но и от способа соединения последних. Предполагается, что элементы находятся в двух состояниях – работоспособном или неработоспособном, а пропускная способность элементов не ограничена.
Суммой двух событий А и В называется событие С, состоящее в выполнении события А или события В или обоих вместе. Если события А и В несовместны, то появление обоих этих событий вместе исключено, и сумма событий А и В сводится к появлению события А или события В. Следовательно, суммой событий А и В называется событие С, состоящее в появлении хотя бы одного из этих событий.
Произведением двух событий А и В называется событие С, состоящее в совместном выполнении события А и события В.
Расчеты надежности систем основаны на использовании основных теорем теории вероятностей.