Вероятность восстановления S(t) — вероятность того, что отказавший элемент будет восстановлен в течение заданного времени t, т. е. вероятность своевременного завершения ремонта.
Очевидно то, что
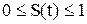 , S(0)=0, S(
, S(0)=0, S( 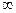 )=1.
)=1.
Для определения величины S(t) используется следующая статистическая оценка:
S(t)= 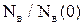 , (4.1)
, (4.1)
где N 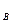 (0) – число элементов, поставленных на восстановление в начальный момент времени t = 0; N
(0) – число элементов, поставленных на восстановление в начальный момент времени t = 0; N 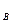 – число элементов, время восстановления которых оказалось меньше заданного времени t, т. е. восстановленных на интервале (0,t).
– число элементов, время восстановления которых оказалось меньше заданного времени t, т. е. восстановленных на интервале (0,t).
Вероятность невосстановления (несвоевременного завершения ремонта) G(t) - вероятность того, что отказавший элемент не будет восстановлен в течение заданного времени t.
Статистическая оценка величины G(t):
G(t)= 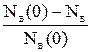 . (4.2)
. (4.2)
Из анализа выражений (4.1) и (4.2) следует, что всегда
S(t)+G(t)=1.
На рис. 4.1 в графической форме представлены изменения S(t) и G(t) во времени.
Частота восстановления a 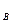 (t) – производная от вероятности восстановления:
(t) – производная от вероятности восстановления:
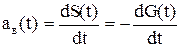 . (4.3)
. (4.3)
Для численного определения величины ав(t) используется её статистическая оценка
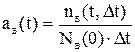 , (4.4)
, (4.4)
где 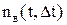 – число восстановленных элементов на интервале времени от t до t +
– число восстановленных элементов на интервале времени от t до t + 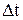 .
.
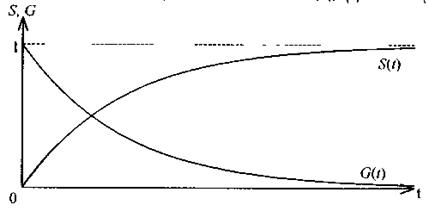
Рис. 4.1
Интенсивность восстановления 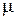 ( t ) — условная вероятность восстановления после момента t за единицу времени
( t ) — условная вероятность восстановления после момента t за единицу времени 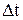 при условии, что до момента t восстановления элемента не произошло.
при условии, что до момента t восстановления элемента не произошло.
Интенсивность восстановления связана с частотой восстановления:
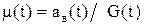 . (4.5)
. (4.5)
Статистически интенсивность восстановления определяется следующим образом:
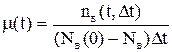 . (4.6)
. (4.6)
Сравнение формул для определения частоты (4.4) и интенсивности (4.6) восстановления показывает, что они отличаются числом элементов в знаменателе.
В отличие от процесса отказов, который развивается во времени естественным образом, процесс восстановления является целиком искусственным (ремонт элемента) и тем самым полностью определяется организационно-технической деятельностью эксплуатационного персонала. Поэтому кривая интенсивности восстановления, аналогичная кривой интенсивности отказов, здесь отсутствует. Так как установлены обоснованные нормативы времени на проведение ремонтных работ, то принимают интенсивность восстановления независимой от времени: 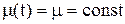 . Численные значения интенсивности восстановления сведены в справочные таблицы по видам оборудования и ремонтов.
. Численные значения интенсивности восстановления сведены в справочные таблицы по видам оборудования и ремонтов.
Для экспоненциального распределения времени восстановления, т.е. при постоянной интенсивности восстановления, по аналогии с процессом отказов (формулы (3.10) и (3.11)) имеем следующие зависимости:
S(t)=1-exp(- 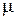 t), (4.7)
t), (4.7)
G(t)=exp(- 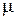 t). (4.8)
t). (4.8)
Среднее время восстановления T 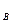 представляет собой математическое ожидание времени восстановления и численно соответствует площади под кривой вероятности невосстановления:
представляет собой математическое ожидание времени восстановления и численно соответствует площади под кривой вероятности невосстановления:
T 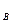 =
= 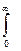 G(t)dt. (4.9)
G(t)dt. (4.9)
Статистическая оценка величины T 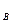 :
:
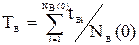 , (4.10)
, (4.10)
где 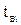 – длительность восстановления i-го элемента (объекта).
– длительность восстановления i-го элемента (объекта).
Для отдельно рассматриваемого элемента под 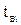 понимается длительность восстановления после i-го отказа, а под
понимается длительность восстановления после i-го отказа, а под 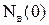 – число отказов данного элемента.
– число отказов данного элемента.
При экспоненциальном распределении времени восстановления, когда интенсивность восстановления 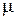 = const, аналогично (3.16) имеем соотношение
= const, аналогично (3.16) имеем соотношение
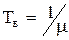 , (4.11)
, (4.11)
т.е. среднее время восстановления численно равно средней по множеству однотипных элементов (объектов) продолжительности восстановления, приходящейся на один объект. Поскольку 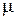 = const, то и T
= const, то и T 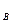 = const.
= const.
В табл. 4.1 сведены показатели надежности, характеризующие процесс выхода из строя элементов, и аналогичные им показатели, характеризующие встречный процесс восстановления элементов.
Таблица 4.1
| Процесс отказов | Процесс восстановления
| ||
| Вероятность безотказной работы | P(t) | Вероятность невосстановления | G(t) |
| Вероятность отказа | Q(t) | Вероятность восстановления | S(t) |
| Частота отказов | a(t) | Частота восстановления | a 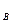 (t) (t)
|
| Интенсивность отказов | 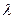 (t) (t)
| Интенсивность восстановления | 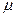 (t) (t)
|
| Средняя наработка на отказ | T | Среднее время восстановления | T 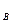
|
В случае, когда требуется оценить надежность работы элемента безотносительно к времени его работы, используются рассматриваемые ниже показатели.








