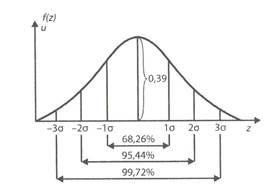
Кривая нормального распределения Гаусса и гистограмма.
Распределением называется закономерность встречаемости признака и разных его значений. Статистическое распределение может иметь графическое представление в виде полигона частот (ломаной линии, соединяющей точки; гистограммы; графика). Кривые распределения бывают одновершинные и многовершинные. Оценка типа распределения выступает в форме проверки нормальности эмпирического распределения. Форма распределения является некоторой обобщенной характеристикой выборки.
Распределение частоты полученных результатов в виде графиков и гистограмм дает важную предварительную информацию о форме распределения признака, а именно о том, какие значения встречаются реже, какие чаще, насколько выражена изменчивость признака. Выделяют следующие типичные формы эмпирического распределения.
Равномерное распределение — когда все значения встречаются с одинаковой частотой.
Симметричное распределение — когда с одинаковой частотой встречаются крайние значения признака.
Асимметричное распределение — может быть левосторонним (когда преобладает частота малых значений) или правосторонним (когда преобладает частота больших значений).
Нормальное распределение — идеальный стандарт распределения, когда крайние значения встречаются редко и частота встречаемости постепенно повышается от крайних к серединным значениям признака.
Нормальный закон распределения играет важнейшую роль в применении математико-статистических методов в психологии. Он лежит в основе измерений, разработки тестовых шкал, методов проверки гипотез.
Нормальное распределение — вид распределения переменных, характеризуемый тем, что крайние значения признака в нем появляются достаточно редко, а значения, близкие к средней величине, — достаточно часто. Нормальным такое распределение называется потому, что оно очень часто встречалось в естественнонаучных исследованиях и казалось «нормой» всякого массового проявления признаков. Это распределение следует закону, открытому в разное время: Муавром в 1733 г. в Англии, Гауссом в 1809 г. в Германии и Лапласом в 1812 г. во Франции.