Вычисление площадей плоских фигур с помощью определенного интеграла

Дата: 2025-06-02; Просмотры: 8

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Повторить вопросы теории.

№1.Вычислите площадь фигуры, ограниченной

линиями:

1) у = 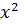и у = 2х+3

2) у = 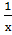, у=0,5 и х=1

3) у = 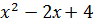и у = 4

№2.Вычислите:

1)

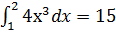
2)

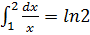
3) 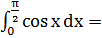1

1. Повторение вопросов теории:

1) Как называется функция F(x) для функции f(x)?

2) Неопределенный интеграл – это…

3) Каким действием можно проверить результат интегрирования?

4) Назовите основные методы интегрирования.

5) Криволинейная трапеция – это…

6) Как называется приращение первообразных функций F(b) –F(a) при изменении аргумента х от х=a до х=b ?

7) В чем заключается геометрический смысл определенного интеграла?

8) Как вычислить площадь фигуры, ограниченной линиями на рисунке?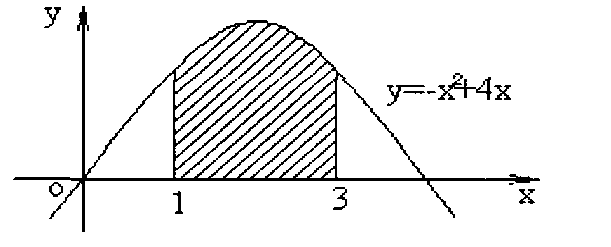

1. Вычисление площади, самое простое применение интеграла, так как интеграл по определению тесно связан с площадью. Повторим основные способы вычисления площади, основные формулы. Алгоритм:

1) Определяем границы плоской фигуры

2) Если границы не указаны, то находим их, решая уравнение f(x) =0 или f(x)=g(х)

3) Строим график функции / функций /

4) Запишем формулу Ньютона-Лейбница.

5) Находим первообразную функции.

6) Вычисляем значение по формуле.

№3.

а. Определить площадь фигуры, образованной функцией у = 2х +5 и осью при изменении х от х=0 до х=3. Ответ: 24 кв.ед.

б. Вычислить площадь фигуры, ограниченной линиями у = .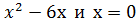

Ответ: 36 кв.ед.

в. Вычислить площадь фигуры, ограниченной линиями у = -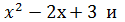

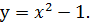Ответ: 9 кв.ед.

Задача, предлагаемая на ЕГЭ

Найдите площадь фигуры, ограниченной графиком функции

у = 2х- 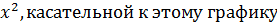, проходящей через точку с абсциссой х =2,

и осью ординат. Подсказка: уравнение касательной: у = f(x₀) - f ΄(x₀)· (x- x₀), где x₀-абсцисса точки касания.

Дополнительно

§ Вычислить площадь фигуры, ограниченной линиями у = 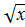, у=6-х, х=0, х=6.

§ Вычислить площадь фигуры, ограниченной линиями у=4х - 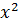, у=0, х=5.

I. Закрепление изученного материала.

Мини- тест. Задания для студентов на оценку «3»

№1. С помощью формулы Ньютона- Лейбница вычисляют:

а) первообразную функция

б) площадь криволинейной трапеции

в) интеграл

г) производную

№2. Вычислите 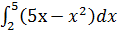Ответы: а) 13,5; б) 10,5; 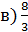; г) 18

№3. Найдите площадь фигуры, ограниченной осью Ох и параболой у = 9-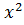

Ответы: а) 18; б) 36; в) 72; г) нельзя вычислить

Задания для студентов на оценку «4» и «5»

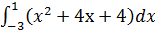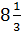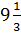№1.Вычислите Ответы: а) ; б) ; в) 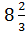; г) 9

№2.Вычислите площадь фигуры, ограниченной линиями у = 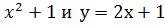Ответы: а) 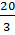; б) ; в)

№3. Вычислите площадь фигуры, ограниченной графиком функции

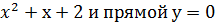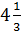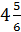у = - . Ответы: а) ; б) ; в) 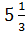; г) 4,5