Практическое занятие №57 (урок 3-4)
20.05.2020
Практическое занятие №57 (урок 3-4)
Рациональные и иррациональные уравнения и неравенства
Задание 1. Вспомните и повторите основные приемы при решении неравенств методом интервалов.(Устно, записывать не нужно)
При решении неравенств методом интервалов важное значение имеет умение раскладывать многочлены на множители. Наиболее часто используются следующие способы:
1. Вынесение за скобки общего множителя.
Примеры:
а)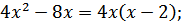 
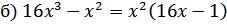
2. Использование формул сокращенного умножения, чаще всего разность квадратов
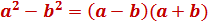
Примеры:
а)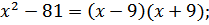 
б)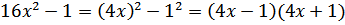 
в)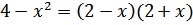 
г)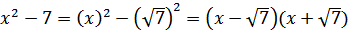 
3. Способ группировки (используется, когда слагаемых четное количество, в частности 4)
Пример
а)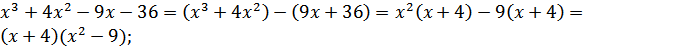 
4. Квадратные трехчлены раскладываются на множители решением соответствующего квадратного уравнения через дискриминант
Пример
.
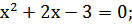
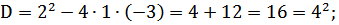
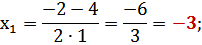
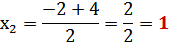
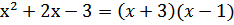Задание 2. Разберите внимательно примеры решения неравенств методом интервалов.
Примеры решения неравенств
| 1. |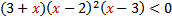 
 (+)
 (-)
 (-)
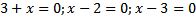
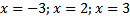
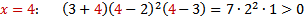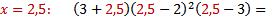
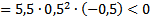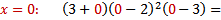
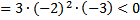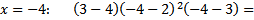
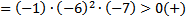Ответ: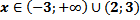 
| 1. Здесь левая часть неравенства уже представлена в виде множителей (раскладывать ничего не нужно) 2. Находим нули функции , стоящей в левой части, т.е. находим, при каких значениях переменной х каждый множитель обращается в нуль. 3. Отмечаем на числовой прямой эти точки и определяем знак на каждом промежутке. Для этого выбираем из каждого промежутка одно число и подставляем его вместо х в исходное неравенство. Так как знак неравенства строгий (<) , то все точки выколотые. 4. Записываем ответ (выписываем промежутки, на которых стоит знак «минус») |
| 2. |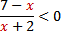 
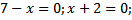
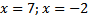
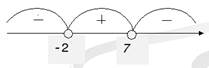
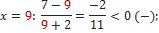
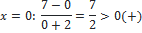
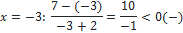Ответ:  .
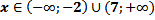| 1. Раскладывать на множители не нужно. 2. Находим точки, в которых числитель и знаменатель обращаются в нуль Отмечаем на числовой прямой эти точки и определяем знак на каждом промежутке. Для этого выбираем из каждого промежутка одно число и подставляем его вместо х в исходное неравенство. Нижняя точка (-2) выколотая; верхняя (7) зависит от знака неравенства: знак неравенства строгий <, точка 7 выколотая. |
| 3 . |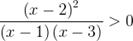 
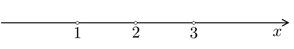
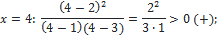
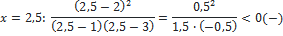
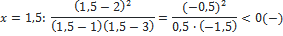
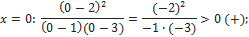
Ответ:  .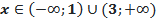
| Здесь решать уравнение не нужно, сразу подбором находим точки, в которых в каждой скобке получится нуль: 2; 1; 3. Их отмечаем на прямой, определяем знаки. Все точки будут выколотые, так как знак неравенства строгий (смотри пояснение выше). Так как знак неравенства стоит >0, то выписываем промежутки с плюсом |
Задание 3. Перепишите в тетрадь примеры 1,2,3 (без пояснений из правого столбика)
Задание 4. Решите самостоятельно: Вариант 1 – первые 9 человек по списку; остальные – вариант 2
На «3» – конспект с тремя переписанными примерами;
на «4» – любые 2 примера; на «5» – все 3 примера
| Вариант1 | Вариант2 | Пояснения | |
| 1 |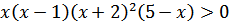 
| 
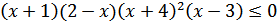
| Здесь будет 4 точки. Вспомните, если х стоит отдельно за скобкой, то это точка 0 |
| 2 |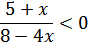 
| 
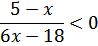
| В знаменателе вынести за скобки общий множитель |
| 3 |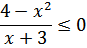 
| 
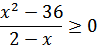
| Здесь будет 3 точки. Числитель разложить на множители по формуле разности квадратов |
Присылаете конспект и самостоятельную работу!