4. Автономный источник энергии
Научно-технические достижения человечества – фантастика, которую теоретики приписывают себе, а экспериментаторы скромно молчат, являясь реальными авторами этих достижений. Новые экспериментальные данные увеличивают указанные разногласия. Наиболее значительные из них - в Динамике и Электродинамике [1].
Из первого закона динамики Ньютона следует, что если тело движется равномерно и прямолинейно, то сумма сил, действующих на него, равна нулю, а если тело вращается равномерно, то сумма моментов, действующих на него, также равна нулю.
Однако, автомобиль, проехав равномерно и прямолинейно, например, 10км., расходует бензин. В результате совершается работа, величину которой можно рассчитать теоретически. Или, если тело вращается равномерно, то на это вращение также расходуется энергия и её тоже можно рассчитать теоретически и определить экспериментально, а первый закон Ньютона отрицает это, утверждая, что сумма моментов, действующих на равномерно вращающееся тело, равна нулю. Это значит, что на равномерное вращение тела энергия не расходуется. Забавно получается, когда начинаешь осознавать, что эти фундаментальные теоретические противоречия спокойно живут столетия и заполняют головы учащейся молодёжи. Теоретики, вместо поиска причин этих противоречий, яростно доказывают их отсутствие [1].
В аналогичном положении находится и электродинамика. Её законы утверждают, что любой потребитель электрической энергии не может выработать её больше, чем получил от первичного источника питания [1]. Достоверность этого утверждения подтверждается всеми техническими устройствами, изобретёнными человеком до 2010г. Они потребляют электрическую энергию от первичного источника и преобразуют её в другие виды энергии, например, в электромеханическую или тепловую с коэффициентом полезного действия меньше единицы. Примером такого устройства является электромеханический генератор электрических импульсов (рис. 45, а). Электромотор (рис. 45, а, вверху) приводит во вращение электрогенератор (рис. 45, а, внизу) с постоянными магнитами. В экспериментах он реализовывал мощность, равную 180Вт. На рис. 45, b – прототип МГ-3.
 а)
а)
|  b )
b )
|
Рис. 45. а) электромеханический генератор электрических импульсов;
b) прототип электромотора-генератора МГ-3
Разность мощности между рабочим и холостым ходом этого электрогенератора, зафиксированная счётчиком электроэнергии на клеммах его электродвигателя, равна 38,90 Вт. Это 21,60% от общей мощности, потребляемой из сети. Очень низкий показатель. Как же улучшить его? Чтобы ответить на этот вопрос, надо установить бесполезных потребителей энергии. Главными из них являются вращающиеся части электромотора и электрогенератора, загруженные напряжением и током первичного источника электроэнергии. Закон Ньютона утверждает, что сумма моментов, действующих на равномерно вращающиеся тела, равна нулю. Это значит, что на равномерное вращение роторов электродвигателя и электрогенератора (рис. 45) не расходуется энергия, а счётчик электроэнергии опровергает это, показывая, что мощность, реализуемая на равномерное вращение указанных роторов на холостом ходу, составляет (100-21,60)=78,40% (рис. 45). Законы механодинамики позволяют рассчитать механическую составляющую этой мощности. Для этого надо знать массу 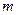 вращающихся частей, их радиусы инерции
вращающихся частей, их радиусы инерции 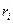 и частоту
и частоту 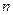 вращения.
вращения.
Связь между кинетической энергией 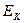 равномерно вращающегося тела и его мощностью
равномерно вращающегося тела и его мощностью 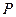 следует из работы, совершаемой им при равномерном вращении за одну секунду (35). Так как мощность генерирует момент сил, то его величина определяется по формуле (36). Формула (36) однозначно отрицает равенство нулю суммы моментов сил, действующих на равномерно вращающееся тело. Из этого следует ошибочность первого закона динамики Ньютона, который выполнял фактически функцию запрещающую поиск резервов снижения затрат электрической энергии на вращение роторов электрогенераторов, питающих своих потребителей.
следует из работы, совершаемой им при равномерном вращении за одну секунду (35). Так как мощность генерирует момент сил, то его величина определяется по формуле (36). Формула (36) однозначно отрицает равенство нулю суммы моментов сил, действующих на равномерно вращающееся тело. Из этого следует ошибочность первого закона динамики Ньютона, который выполнял фактически функцию запрещающую поиск резервов снижения затрат электрической энергии на вращение роторов электрогенераторов, питающих своих потребителей.
Механическое сопротивление вращению ротора формирует его момент инерции, а ток, протекающий по обмотке ротора, может усиливать или ослаблять это сопротивление. Поэтому возникает необходимость установить физические факторы, усиливающие сопротивление вращению ротора и ослабить их действие или полностью ликвидировать.
На рис. 46. представлена осциллограмма напряжения и тока, снятая с клемм электромеханического генератора электрических импульсов (рис. 45) и электролизёра. Поскольку между их клеммами лишь провода, то осциллограмма напряжения и тока у них едина.
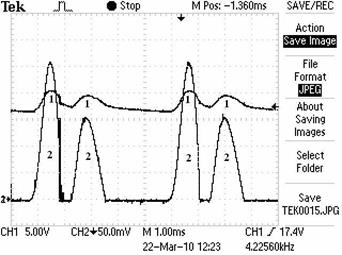
Рис. 46. Осциллограмма импульсов напряжения (1) и тока (2) на клеммах
электромеханического генератора электрических импульсов и электролизёра
Обработка этой осциллограммы показала, что скважность импульсов напряжения равна, примерно, 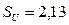 , а тока -
, а тока - 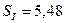 . Средние величины напряжения
. Средние величины напряжения 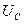
 и тока
и тока 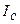 определяются делением их амплитудных значений
определяются делением их амплитудных значений 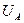 ,
, 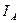 на скважность импульсов. Осциллограмма даёт нам такие значения:
на скважность импульсов. Осциллограмма даёт нам такие значения: 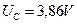 ,
, 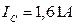 . С учётом этого средняя мощность на клеммах электрогенератора равна
. С учётом этого средняя мощность на клеммах электрогенератора равна
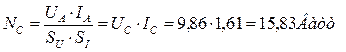 , (52)
, (52)
а он забирает из сети 180Вт, то есть в (180/15,83)=11,37 раз больше. За час работы, при которой электромотор приводил в действие электрогенератор, питающий электролизёр, было получено 15,40 литра газовой смеси: водорода и кислорода. Это значит, что удельные затраты по показаниям счётчика электроэнергии составили 180/15,40=11,70 Вт/литр, а прямые удельные затраты энергии (без учета всех потерь), следующие из формулы (52) составили 15,83Втч/15,40=1,03 Втч/литр.
Из этого следует, что для уменьшения потерь электроэнергии на процесс электролиза воды надо сложную конструкцию, состоящую из электромотора и электрогенератора (рис. 45) упростить до состояния, при котором роль электромотора выполнял бы ротор, а роль генератора – статор. Такой электромотор-генератор впервые был создан в России в 2010г и дал обилие новой экспериментальной информации, неведомой ранее. На рис. 47 представлен электромотор – генератор МГ-1 без постороннего привода. Роль мотора у него выполняет ротор, а роль генератора – статор.

Рис. 47. Фото электромотора - генератора МГ-1 без постороннего привода
Он проектировался для питания от сети, но оказалось, что может питаться и от аккумуляторов, если их общее напряжение соизмеримо с напряжением сети. На рис. 47 представлены: МГ-1, ячейка электролизера и две группы аккумуляторов, каждая из 4-х 12-ти вольтовых мотоциклетных аккумуляторов 6МТС-9. Получая электроэнергию от одной группы аккумуляторов для вращения своего ротора, МГ-1 заряжает другую группу аккумуляторов и одновременно питает электролизёр. В результате образуется автономный источник энергии, который можно использовать для проверки законов динамики и электродинамики. Начнём с законов динамики. В чём суть ошибочности первого закона динамики?
Ньютон поставил на первое место в своей динамике закон равномерного движения твёрдого тела, которое всегда появляется после ускоренного движения любого тела и поэтому является его следствием. В реальности причина всегда первична, а следствие этой причины – вторично, поэтому на первое место надо было поставить закон ускоренного движения, а на второе – равномерного. Эта ошибка Ньютона уже исправлена в механодинамике, полная разработка которой ещё не завершена [1]. Но законы механодинамики уже систематизированы и их можно использовать для последовательного описания ускоренного, равномерного и замедленного движений или вращений твёрдых тел, которые они совершают в реальности. Ротор МГ-1 вращается равномерно. Первый закон динамики Ньютона утверждает, что в этом случае сумма моментов, действующих на него, равна нулю. Результаты проведённых экспериментов показывают ошибочность такого утверждения. Вот её суть.
Масса ротора электромотора-генератора МГ-1 равна 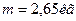 , радиус инерции ротора равен
, радиус инерции ротора равен 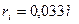 . В данном эксперименте ротор вращался с частотой
. В данном эксперименте ротор вращался с частотой 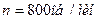 . Связь между кинетической энергией
. Связь между кинетической энергией 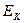 равномерно вращающегося ротора МГ-1 и его мощностью
равномерно вращающегося ротора МГ-1 и его мощностью 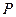 следует из работы, совершаемой им при равномерном вращении за одну секунду (35)
следует из работы, совершаемой им при равномерном вращении за одну секунду (35)
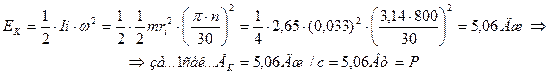 . (53)
. (53)
Из результата, представленного в формуле (53) следует мощность, реализуемая непрерывно первичным источником питания на привод ротора МГ-1. Однако, все электрогенераторы генерируют электроэнергию путём периодического взаимодействия магнитных полюсов роторов и статоров. Встаёт вопрос: нельзя ли использовать момент инерции 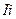 ротора для перевода непрерывного процесса подачи электроэнергии в его обмотку возбуждения в импульсный процесс? Оказывается можно. В результате появляется возможность ещё больше уменьшить мизерную мощность 5,06Вт (53), подаваемую в обмотку возбуждения ротора в количество раз, равное скважности механических импульсов взаимодействия магнитных полюсов ротора и статора.
ротора для перевода непрерывного процесса подачи электроэнергии в его обмотку возбуждения в импульсный процесс? Оказывается можно. В результате появляется возможность ещё больше уменьшить мизерную мощность 5,06Вт (53), подаваемую в обмотку возбуждения ротора в количество раз, равное скважности механических импульсов взаимодействия магнитных полюсов ротора и статора.
В соответствии с законами механодинамики, равномерное вращение ротора МГ-1 всегда следует после ускоренного вращения. Осциллограмма изменения пускового момента ротора убедительно доказывает это (рис. 40).
Если бы электрическая энергия подавалась в обмотку возбуждения ротора МГ-1 непрерывно, то на его равномерное вращение требовалось бы 5,06Вт (53). При импульсной подаче электроэнергии в обмотку возбуждения ротора со скважностью импульсов 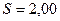 требуется меньшая электрическая мощность 5,06/2,00=2,53 Вт. Однако механическая мощность постоянно действующая на валу ротора при его равномерном вращении, генерирует механический момент, рассчитываемый по формуле
требуется меньшая электрическая мощность 5,06/2,00=2,53 Вт. Однако механическая мощность постоянно действующая на валу ротора при его равномерном вращении, генерирует механический момент, рассчитываемый по формуле
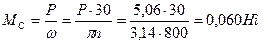 . (54)
. (54)
Таким образом, ошибочность первого закона Ньютона очевидна. Сумма моментов, действующих на равномерно вращающийся ротор, равна 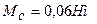 , а не нулю, как утверждает первый закон бывшей динамики Ньютона.
, а не нулю, как утверждает первый закон бывшей динамики Ньютона.
А теперь начнём совместную проверку достоверности закона электродинамики, который запрещает электромеханическому источнику энергии вырабатывать её больше той, какую он получает от первичного источника, в данном случае, от аккумуляторов, а первый закон динамики Ньютона запрещает участие в этом процессе вращающихся частей такого генератора.
Суть экспериментальной проверки достоверности указанных законов проста. Берём две группы из 4-х 12-ти вольтовых мотоциклетных аккумуляторов. Подаём из первой группы напряжение в обмотку возбуждения ротора МГ-1 импульсами. В ней формируются два импульса: ЭДС индукции и ЭДС самоиндукции. Снимаем эти импульсы и направляем на зарядку второй группы таких же аккумуляторов. При периодическом изменении процессов разрядки на процессы зарядки этих аккумуляторов, образуется автономный источник электроэнергии, в обмотке статора которого также формируются два электрических импульса: импульс ЭДС индукции и импульс ЭДС самоиндукции. Эти импульсы можно использовать на питание технологических процессов, например, процесса электролиза воды (рис. 47).
Пробные эксперименты показали, что такой автономный источник энергии производит её больше, чем потребляет от первичного источника питания. Возникло искушение проверить его в длительном режиме: разрядка аккумуляторов + зарядка аккумуляторов + получение смеси газов водорода и кислорода при электролизе воды.
Приборы показали, что ток зарядки аккумуляторов равен 0,19А, а ток разрядки – 0,65А. Стало ясно, что долго такой автономный источник энергии не проработает.
Подключив дополнительное сопротивление, увеличили ток зарядки до 0,26А. Анализ показал, что для достижения равенства между током зарядки и разрядки необходимо изменить обмотку возбуждения ротора, которая генерирует два импульса: импульс ЭДС индукции и импульс ЭДС самоиндукции. Оба они участвуют во вращении ротора и зарядке аккумуляторов. На холостом ходу ротора амплитуды и длительности этих импульсов отличаются в десятки раз. В режиме зарядки аккумуляторов длительности и амплитуды обоих импульсов почти выравниваются.
Стало ясно, что в таких условиях невозможно рассчитать параметры обмотки ротора, обеспечивающие равенство токов разрядки и зарядки аккумуляторов. Решить эту задачу можно только экспериментально. Встал вопрос: что делать? Менять обмотку ротора или провести эксперимент пока при тех параметрах, какие есть. Его результаты, несомненно, будут интересны не только авторам эксперимента, но и читателям наших интернетовских публикаций. Они представлены в табл. 4.
Большее падение напряжения на аккумуляторах первой группы обусловлено низким напряжением на клеммах новых аккумуляторов №1 и №4, которое может быть следствием замыкания между пластинами. Вполне естественно, что бракованные аккумуляторы №1 и №4 исключали возможность продолжения эксперимента, и он был остановлен.
Из таблицы 4 следует, что напряжение на клеммах 2-й группы аккумуляторов уменьшилось от недозарядки и опустилось за 25 часов до 45,40В. Поскольку нижний уровень равен 44,00В, то есть основания полагать, что при нормальных аккумуляторах в обоих группах МГ-1 сможет проработать непрерывно до 30-35 часов при существующей разнице между током разрядки и зарядки.
Таблица 4. Результаты 25-ти часовых испытаний МГ-1
в режиме «вечного» электрогенератора
| Циклы и часы работы | Общее напряжение первой группы аккумуляторов, В | Общее напряжение второй группы аккумуляторов, В |
| 1 | 50,70-49,60 – разрядка | 50,60-51,00 - зарядка |
| 2 | 49,60-51,00 – зарядка | 51,00-49,80 – разрядка |
| …….. | ……… | …….. |
| Через 1 час | 51,00-48,40 – разрядка | 49,60-51,00 – зарядка |
| ……… | ……… | …. |
| Через 10 часов | 51,00-46,60 – разрядка | 47,70-51,00– зарядка |
| …… | ………. | ………… |
| Через 20 часов | 41,90-50,60 – зарядка | 49,50-45,60 - разрядка |
| ……… | ……. | …… |
| Через 25 часов | 50,20-41,00 - разрядка | 45,40-48,30 - зарядка |
| За 25 часов получено 10 литров смеси газов водорода и кислорода (0,40л/час) | ||
Причина разбалансировки процессов разрядки и зарядки аккумуляторов первой и второй групп следует из таблицы 5.
Таблица 5. Напряжение на клеммах аккумуляторов в режиме разрядки
| Первая группа аккумуляторов | Вторая группа аккумуляторов | ||
| Номера аккумуляторов | Напряжение, В | Номера аккумуляторов | Напряжение, В |
| 1 | 9,45 | 5 | 11,28 |
| 2 | 11,12 | 6 | 11,35 |
| 3 | 11,35 | 7 | 11,38 |
| 4 | 9,93 | 8 | 11,69 |
Итак, первый эксперимент работы МГ-1 в условном режиме «вечного» электрогенератора показывает возможность создания автономного источника энергии со сроком службы, равным сроку службы аккумулятора.
МГ-1 работает в автономном режиме и не потребляет энергию из сети, поэтому затраты энергии на электролиз воды этим генератором можно определить лишь из осциллограммы. Для этого проанализируем баланс электрической мощности МГ-1, используя математические модели старого (32) и нового (31) законов формирования импульсной электрической мощности.
Осциллограммы импульсов напряжения и тока показывают, что в соответствии со старым законом (32) формирования импульсной электрической мощности аккумуляторы реализуют на привод ротора 32,76Вт. В соответствии с новым законом (31) они реализовывали 7,50Вт при том же токе разрядки. Но это только электрическая мощность, к ней надо прибавить механическую мощность, постоянно присутствующую на валу равномерно вращающегося ротора. Тогда общая мощность на валу ротора будет равна 7,50+5,06=12,56Вт. Эта электрическая мощность расходуется на формирование импульсов механических моментов 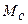 , вращающих ротор, а также на зарядку аккумуляторов и на электролиз воды. Так как функции напряжения и тока зарядки аккумуляторов непрерывны (рис. 48), то старый и новый законы формирования мощности, реализуемой на зарядку аккумуляторов, дают один и тот же результат
, вращающих ротор, а также на зарядку аккумуляторов и на электролиз воды. Так как функции напряжения и тока зарядки аккумуляторов непрерывны (рис. 48), то старый и новый законы формирования мощности, реализуемой на зарядку аккумуляторов, дают один и тот же результат 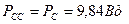 .
.
Поскольку в формировании баланса мощности на валу ротора МГ-1 участвуют импульсы ЭДС самоиндукции статора и ротора, то пока не существует точных методов расчёта такого баланса. Поэтому остаётся одно – привести примерный его результат. Согласно старому закону (32) аккумуляторы реализуют на привод ротора электромотора – генератора 32,76Вт, а нового (31) – 7,50+5,06=12,56Вт. На зарядку аккумуляторов расходуется 9,84Вт, а на электролиз воды 2,34Вт и 0,76Вт соответственно.
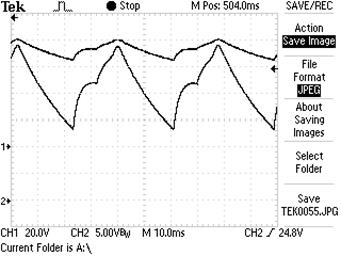
| На клеммах аккумуляторов:
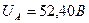 ; ;
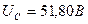 ; ;
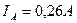 ; ;
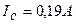 .
Расчётные данные: .
Расчётные данные:
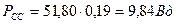 ; ;
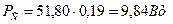 . .
|
Рис. 48. Осциллограмма на клеммах заряжаемых аккумуляторов
Таким образом, согласно старому закону (32) формирования импульсной электрической мощности, мощность на входе в МГ-1 равна 32,76Вт, а на выходе – (2,53+9,84+2,34)=14,71Вт, то есть мощность на входе в 32,76/14,71=2,23 раза больше мощности на выходе. Однако, более правильным будет учёт мощности на входе МГ-1, идущей от аккумуляторов и мощности на их зарядку. В этом случае мощность на входе в 32,76/9,24=3,33 раза больше мощности на выходе, то есть аккумуляторы отдают на питание МГ-1 мощность в 3,33 раза большую, чем получают от него на свою зарядку. Это полностью исключает длительную (25 часов) работу МГ-1 в автономном режиме. Новый закон (31) даёт другой результат: на входе 7,50Вт, а на выходе (2,53+9,24+0,76)=12,53Вт. Из этих результатов следует, что согласно новому закону (31) мощность на выходе МГ-1 в 12,53/7,50=1,67 раза больше мощности на входе, реализуемой аккумуляторами на привод МГ-1. Это обусловлено участием импульсов ЭДС самоиндукции ротора и статора, на которые почти не расходуется энергия аккумуляторов.
Подключение к аккумуляторам лампочек с общей мощностью 31Вт. Показало, что они разряжают аккумуляторы в линейном диапазоне (48,00-47,00В) в 2,66 раза быстрее. Разделив 32,76Вт на общую мощность на валу ротора 12,56Вт, имеем 2,61. Этот результат близок к 2,66, поэтому есть основания для признания ошибочности старого закона формирования средней электрической импульсной мощности. Этот вывод полностью подтверждают результаты эксперимента, представленные в табл. 4.
После изменения длительности импульсов и моментов начала их включения и выключения эксперимент, описанный в статье «Начало импульсной энергетики», был продолжен. Ток разрядки аккумуляторов в начале эксперимента 0,42А, а ток зарядки – 0,21А. Обмотка ротора не перематывалась.
Таблица 6. Результаты 70-ти часовых испытаний МГ-1
в режиме «вечного» электрогенератора
| Часы работы | Общее напряжение первой группы аккумуляторов, В | Общее напряжение второй группы аккумуляторов, В |
| Через 1 час | 51,50-50,00 – разрядка | 50,20-52,00 – зарядка |
| Через 10 часов | 51,00-49,30 – разрядка | 49,10-51,50– зарядка |
| Через 20 часов | 48,60-50,50 – зарядка | 50,00-48,40 - разрядка |
| Через 30 часов | 49,70-48,00 - разрядка | 48,00-50,10 - зарядка |
| Через 40 часов | 49,50-47,30 - разрядка | 49,90-47,50 - разрядка |
| Через 50 часов | 46,90-48,90 - зарядка | 49,30-46,80 - разрядка |
| Через 60 часов | 48,60-46,10 - разрядка | 48,90-46,10 - разрядка |
| Через 70 часов | 41,80-47,70 - разрядка | 48,20-41,40 - разрядка |
| За 70 часов получено 43 литра смеси газов водорода и кислорода (0,60л/час) | ||
Причина разбалансировки процессов разрядки и зарядки аккумуляторов первой и второй групп следует из таблицы 7.
Таблица 7. Напряжение на клеммах аккумуляторов в режиме разрядки через 70 часов непрерывной работы
| Первая группа аккумуляторов | Вторая группа аккумуляторов | ||
| Номера аккумуляторов | Напряжение, В | Номера аккумуляторов | Напряжение, В |
| 1 | 11,03 | 5 | 11,40 |
| 2 | 11,57 | 6 | 11,47 |
| 3 | 7,99 | 7 | 10,77 |
| 4 | 11,64 | 8 | 11,74 |
Аккумуляторы № 1,2,4 – ОАО Тюменского аккумуляторного завода.
Аккумуляторы № 3, 5, 6, 7 и 8 – ОАО «Электроисточник» г. Саратов.
Теоретический расчёт показывает, что при одинаковом высоком качестве всех аккумуляторов МГ- проработал бы в, так называемом, линейном диапазоне разрядки каждого аккумулятора (12,50-11,00)В около 90 часов.
Средняя мощность на клеммах ячейки электролизёра была равна 0,31Вт. Удельные прямые затраты на получение одного литра смеси водорода и кислорода составили 0,31/0,60=0,52Втч/л.
ЗАКЛЮЧЕНИЕ
Результаты длительного эксперимента доказывают ошибочность первого закона динамики Ньютона и ошибочность старого закона электродинамики, описывающего формирование средней величины импульсной электрической мощности. Новые законы механодинамики уже систематизированы [1]. Разработаны основы и новой электродинамики [1], которые уже вступили в стадию реализации при разработке электромоторов-генераторов МГ-1 и МГ-2. Достоверность нового закона формирования средней импульсной электрической мощности уже доказана серией различных экспериментов.
5. ВОДА – ИСТОЧНИК ВОДОРОДА И КИСЛОРОДА
Вводная часть
Исчерпаемость существующих энергоносителей и ухудшающаяся экологическая обстановка сформировали понимание необходимости перехода на неисчерпаемую и экологически чистую водородную энергетику [33], [37], [38], [39], [46], [47].
В решение этой проблемы включились не только ученые, но и политики, поэтому желательно иметь более четкое представление о проблемах начального периода. Вода является самым ёмким накопителем энергии, поэтому на неё, как основной источник энергии, и возлагаются главные надежды. Уже разработаны технологии получения дополнительной энергии из воды в виде тепла, электричества и газов: водорода и кислорода, но они ещё малопроизводительны. Существовавшие до этого знания о микромире, в том числе и о молекулах, и кластерах воды не позволяли видеть перспективу значительного улучшения уже достигнутых показателей. Однако, новые знания о микромире такую возможность предоставляют и мы покажем её реализацию на простых лабораторных установках.
Вполне естественно, что уже достигнутые результаты открывают широкую перспективу использования воды, как источника энергии. Это вдохновляет и тревожит. Мы пока не знаем последствий этого направления для сохранения сложившегося баланса водных ресурсов нашей планеты. Хотя уже ясно, что новое энергетическое направление ослабит экологическую нагрузку на водные бассейны и среду обитания человека. Учитывая изложенное, приступим к анализу процесса электролиза воды с целью снижения затрат энергии на получение водорода и кислорода. Опишем серию экспериментов, которые показывают, что вода может разлагаться на водород и кислород с показателем энергетической эффективности, значительно больше единицы, если учёт электроэнергии импульсными потребителями будут вести новые счётчики электроэнергии.
Явное нарушение самого фундаментального закона физики – закона сохранения энергии, потребовало поиска причин возникших противоречий между теорией и экспериментом, но выполнить такой поиск, как мы уже описали, оказалось не так просто. Получалось так, что Природа разлагает воду на водород и кислород при фотосинтезе многократно экономнее, чем это делает человек, и её никто не упрекает в нарушении закона сохранения энергии. Поэтому первая задача на этом пути – найти причину, которая сдерживает наши возможности повторить достижения Природы в экономии энергии, затрачиваемой на разложение воды на водород и кислород.
Мы уже отметили одну из таких причин – ошибочность электротехнического закона сохранения энергии, математические модели которого заложены в программы всех измерительных приборов, учитывающих её потребление. Поэтому первейшая задача водородной энергетики – разработка новых счётчиков электроэнергии, которые бы правильно учитывали импульсное её потребление. Это откроет путь для разработки и применения экономных импульсных генераторов электрической энергии и импульсных её потребителей. Мы уже привели информацию о первых импульсных электромоторах – генераторах МГ-1 и МГ-2. Сейчас представим серию экспериментальных данных по импульсному электролизу воды, из которых следует экономичность этого процесса, питаемого электромоторами – генераторами. Мы не будет упоминать о них, так как опыты проводились до создания таких генераторов с помощью электромеханических и электронных генераторов электрических импульсов.
Сейчас наиболее совершенные промышленные электролизёры расходуют около 4 кВтч электроэнергии на получение одного кубического метра водорода из воды. При сжигании этого водорода может выделиться около 3,5 кВтч чистой энергии. Из этого следует, что водород может стать конкурентно-способным энергоносителем, если затраты энергии на его получение из воды сделать значительно меньшими энергии, получаемой при его сжигании. Мы покажем на серии экспериментов, что эта задача успешно решается при переходе на импульсную энергетику.
Нетрудно представить, какие финансовые и интеллектуальные ресурсы мира включены в решение этой задачи. В России этой проблемой занимаются многие научные учреждения отраслевой науки, существует научно-исследовательский водородный институт. В США и Европе созданы ассоциации ученых по водородной энергетике.
Решение задачи снижения затрат электрической энергии на получение водорода из воды должно начинаться с анализа резервов снижения этих затрат существующими электролизёрами. Они скрыты в постоянном потенциале электролизёров и мы покажем метод использования этого потенциала для снижения затрат электрической энергии на получение водорода из воды.
Но самый большой резерв снижения затрат энергии на электролиз воды скрыт в процессе фотосинтеза. Ежегодно при этом процессе растения выделяют из воды сотни миллионов кубометров водорода, атомы которого используются, как соединительные звенья при строительстве органических молекул. Для реализации этого процесса все живые организмы имеют собственные очень экономные источники энергии.
А что если смоделировать указанный процесс в техническом устройстве? Тогда образующийся водород, не имея возможности участвовать в строительстве органических молекул, будет вместе с кислородом выходить в атмосферу. Устройства для локализации и разделения этих газов уже существуют. Главное условие, при котором идет указанный процесс электролиза воды, – небольшая величина среднего тока при большой амплитуде его импульса.
Уже получены патенты на ряд таких устройств и их можно увидеть в действии. Конечно, это пока небольшие малопроизводительные лабораторные модели, но они устойчиво разлагают воду на водород и кислород при среднем токе 0,02-0,03 Ампера, а также и при отключенном внешнем источнике питания.
Установлено, что зарядка такого электролизера идет несколько минут. После этого его можно отключать от сети и он будет разлагать воду на водород и кислород без постореннего источника питания. Этот процесс легко наблюдается по выходу пузырьков газов в течение нескольких часов после отключения электролизёра от сети. Из этого следует, что нет нужды держать электролизёр включенным в электрическую сеть непрерывно. Для поддержания такого электролизёра в рабочем состоянии его достаточно подключать к источнику питания периодически.
Одновременно на электродах такого электролизёра появляется напряжение и его можно использовать, как источник электрической энергии. Владея всей нашей научной информацией по этому вопросу, имея неограниченное финансирование и - природную скрупулёзность в стремлении к совершенству сделанного, японские исследователи уже имеют автомобиль, работающий на электричестве, получаемом не из топливного элемента, а из электролизёра.
5.1. Противоречия существующей теории электролиза воды
Полезность любой теории определяется её возможностями правильно интерпретировать результаты уже существующих экспериментов и прогнозировать возможность получения новых теоретических и экспериментальных данных. Посмотрим, отвечает ли этим требованиям, существующая теория электролиза воды [5], [6], [8], [9], [10], [11], [12], [14], [15]. [19], [20], [23], [24], [29], [31]? Для этого, проанализируем классический способ получения водорода при электролизе воды. Он описан в многочисленных учебниках. Химические реакции, протекающие при этом процессе, используются для расчетов его параметров. Они признаются предельно ясными и не вызывают возражений как среди химиков, так и среди физиков. Посмотрим, действительно ли здесь все так ясно?
Вот как описываются катодные и анодные реакции в учебнике [2]. "На катоде протекает следующая реакция:
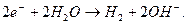 (55)
(55)
Два электрона, поступающие с катода, реагируют с двумя молекулами воды, образуя молекулу водорода 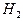 и два иона гидроксила
и два иона гидроксила 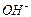 . Молекулярный водород образует пузырьки газообразного водорода (после того, как раствор вблизи катода насытится водородом), а ионы гидроксила остаются в растворе.
. Молекулярный водород образует пузырьки газообразного водорода (после того, как раствор вблизи катода насытится водородом), а ионы гидроксила остаются в растворе.
На аноде протекает реакция
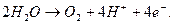 (56)
(56)
Четыре электрона переходят на анод с двух молекул воды, которая разлагается с образованием молекулы кислорода и четырех ионов водорода.
Суммарную реакцию можно получить, умножая уравнение (56) на 2 и суммируя с уравнением (56). Она выглядит следующим образом:
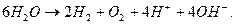 (57)
(57)
... в кислых растворах, с высокой концентрацией ионов водорода, на катоде может просто протекать реакция
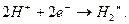 (58)
(58)
Закроем кавычки и зададим такой вопрос: что следует понимать под символом 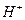 при таком изложении сути процесса электролиза воды? Естественно,
при таком изложении сути процесса электролиза воды? Естественно, 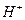 означает положительный ион атома водорода, то есть протон. Однако химики умудрились обозначить этим же символом и положительно заряженный ион гидроксония
означает положительный ион атома водорода, то есть протон. Однако химики умудрились обозначить этим же символом и положительно заряженный ион гидроксония 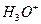 . Они давно приняли соглашение: в целях упрощения записи, писать
. Они давно приняли соглашение: в целях упрощения записи, писать 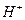 , вместо -
, вместо - 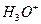 . Вот и приходится гадать: всегда ли под химическим символом
. Вот и приходится гадать: всегда ли под химическим символом 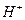 надо понимать совокупность символов
надо понимать совокупность символов 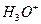 или нет? А если нет, то, как же различать случаи "да" и "нет"? Ведь символ
или нет? А если нет, то, как же различать случаи "да" и "нет"? Ведь символ 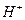 используется в многочисленных других химических реакциях.
используется в многочисленных других химических реакциях.
Если согласиться с процессом электролиза, описанным в приведенном учебнике, то из него следует, что в водном растворе существуют протоны, которые автор обозначает символом 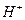 . Имея положительный заряд, они движутся к катоду и, получив от него электрон
. Имея положительный заряд, они движутся к катоду и, получив от него электрон 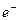 , образуют вначале атомы водорода
, образуют вначале атомы водорода 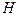 , которые, соединяясь, формируют молекулы
, которые, соединяясь, формируют молекулы 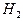 , выделяя при этом 436 кДж/моль. По-другому ведь невозможно интерпретировать формулы (56), (57), (58).
, выделяя при этом 436 кДж/моль. По-другому ведь невозможно интерпретировать формулы (56), (57), (58).
Кроме того, из формул (57, 58) следует, что у анода идет процесс синтеза молекул кислорода из его атомов, который должен сопровождаться выделением энергии 495 кДж/моль [2]. Это также надо учитывать при анализе энергетического баланса процесса электролиза воды, но в современной химии не принято проводить такой анализ, так как из него следуют противоречия с экспериментом. Рассмотрим одно из них.
Введем, как это и должно быть, символ 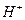 для обозначения только протона. Тогда реакция синтеза атома водорода
для обозначения только протона. Тогда реакция синтеза атома водорода 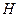 запишется так
запишется так
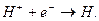 (59)
(59)
Реакция синтеза молекулы водорода представится в виде
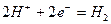 . (60)
. (60)
Гипотеза о присутствии в различных химических растворах свободных протонов атомов водорода плодотворно используется в химии. Однако появление плазменного электролиза воды ставит эту гипотезу под сомнение. Дело в том, что протон - это очень маленькое и очень активное образование, которое может существовать только в составе ядра атома или в составе атома водорода, выполняя роль его ядра. Атом водорода имеет такую структуру, которая обеспечивает ему реализацию функций идеального звена (рис. 4), соединяющего атомы в молекулы.
Таким образом, в электролитическом растворе у протона почти отсутствует фаза существования в свободном состоянии. Отделившись от одного химического элемента, он тут же соединяется с другим.
При плазменном электролизе воды формируются такие условия, когда протон атома водорода, отделившись от молекулы воды, соединяется с электроном, испущенным катодом, и образует атом водорода. Известно, что атомы водорода существуют в свободном состоянии при температуре (2700...10000) 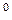 С [13]. Это означает, что при определенной плотности атомов водорода в единице объема должна формироваться плазма с такой температурой. Но при низковольтном электролизе воды плазма атомарного водорода, как известно, не образуется. Это значит, что в этом случае отсутствуют условия существования атомов водорода в свободном состоянии, то есть условия синтеза атомов водорода.
С [13]. Это означает, что при определенной плотности атомов водорода в единице объема должна формироваться плазма с такой температурой. Но при низковольтном электролизе воды плазма атомарного водорода, как известно, не образуется. Это значит, что в этом случае отсутствуют условия существования атомов водорода в свободном состоянии, то есть условия синтеза атомов водорода.
В современной химии известна энергия синтеза молекул водорода (436 кДж/моль), поэтому мы можем рассчитать примерное количество энергии, которое должно выделяться в электролитическом растворе при получении одного кубометра водорода в условиях, когда свободные атомы водорода объединяются в молекулы, как это следует из старой теории электролиза воды (55-59) [2], [7], [13]. В одном кубическом метре водорода содержится 1000/22,4=44,64 моля молекулярного водорода. При его синтезе выделяется энергия
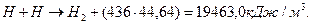 (61)
(61)
Современные лучшие электролизеры расходуют на получение одного кубического метра водорода около 4 кВтч электроэнергии или (3600х4) = 14400 кДж. Учитывая энергию (19463,0 кДж) синтеза одного кубического метра водорода и энергию (14400 кДж), затрачиваемую на его получение, находим показатель тепловой энергетической эффективности низковольтного процесса электролиза воды, следующий из старой теории электролиза воды.
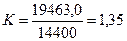 . (62)
. (62)
Таким образом, простой и строгий расчет показывает, что процесс низковольтного электролиза воды, следующий из его старой теории, должен сопровождаться выделением 35% дополнительной тепловой энергии только в зоне катода.
Обратим внимание на то, что показатель эффективности (62) учитывает только энергию синтеза молекул водорода и не учитывает энергию синтеза атомов водорода и молекул кислорода, а также энергосодержание полученного водорода. Этот показатель (62) подтверждает возможность получения дополнительной энергии, но при условии, чтобы электролиз воды сопровождался процессом синтеза молекул водорода. Отсутствие дополнительной тепловой энергии в работе современных промышленных электролизеров вынуждает нас делать вывод об отсутствии при этом процессе синтеза молекул водорода из его атомов.
Если согласиться с наличием процесса синтеза молекул кислорода, то в зоне анода должна протекать реакция
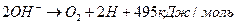 , (63)
, (63)
то есть должны формироваться молекулы кислорода и атомы 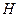 водорода. Но, как известно, при низковольтном электролизе воды в зоне анода выделяется только кислород.
водорода. Но, как известно, при низковольтном электролизе воды в зоне анода выделяется только кислород.
Известно также, что при низковольтном процессе электролиза воды формирование 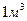 (44,64 моля) водорода сопровождается выделением 22,32 моля молекулярного кислорода. В результате этого должно выделяться 495х22,32=11048,80 кДж энергии. Складывая эту энергию с энергией синтеза молекул водорода, получим
(44,64 моля) водорода сопровождается выделением 22,32 моля молекулярного кислорода. В результате этого должно выделяться 495х22,32=11048,80 кДж энергии. Складывая эту энергию с энергией синтеза молекул водорода, получим
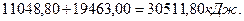 (64)
(64)
Тогда общий показатель тепловой энергетической эффективности низковольтного процесса электролиза воды с учётом энергии, выделяющейся в зонах катода и анода, должен быть таким
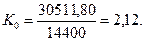 (65)
(65)
Но в реальности его нет. Тепловой энергетический показатель современного низковольтного процесса электролиза воды меньше единицы, поэтому возникает вопрос: каким образом формируются молекулы водорода и кислорода при низковольтном процессе электролиза воды, не генерируя ту энергию, которая следует из старой теории этого процесса (61 и 63)? Ответа нет [2].
5.2. Новая теория электролиза воды и её экспериментальная проверка
Вооружившись полученной информацией, приступим к поиску новой теории существующего процесса электролиза воды. Эта теория должна ответить, прежде всего, на следующий вопрос: почему теоретические расчеты показывают наличие дополнительной тепловой энергии при низковольтном электролизе воды, а существующие промышленные электролизеры не генерируют её?
Поскольку атомарный водород существует лишь при температуре 2700-10000 С, а в обычных электролизёрах такой температуры нет, то это значит, что при электролизе воды отсутствует процесс синтеза молекул водорода из его свободных атомов и сразу возникает вопрос откуда берутся молекулы водорода при электролизе воды? Почему наши предшественники не поставили этот вопрос? Мешало орбитальное движение электронов в атомах, которое лишало возможности формирования правильных представлений о процессах соединения атомов в молекулы. Теперь мы знаем, что электроны взаимодействуют с протонами ядер не орбитально, а линейно [51]. Отсутствие орбитального движения электронов в атомах и их линейное взаимодействие с протонами ядер раскрывает структуры любых атомов, в том числе и атомов водорода (рис. 4) и кислорода (рис. 49, b), которые входят в состав молекулы воды.
Отметим ещё раз: атомарный водород (рис. 4) существует в плазменном состоянии при температуре 2700-10000 С. Если бы образование молекул водорода при электролизе воды шло путем отделения его атомов от молекул воды, то в фазе атомарного состояния водорода в электролитическом растворе должна формироваться указанная температура, но её нет, поэтому у нас появляются основания предположить, что молекулы водорода и кислорода выделяются из кластеров воды в синтезированном состоянии. Плодотворность этого предположения подтверждают структуры атома кислорода (рис. 49, b) и молекулы воды (рис. 50).
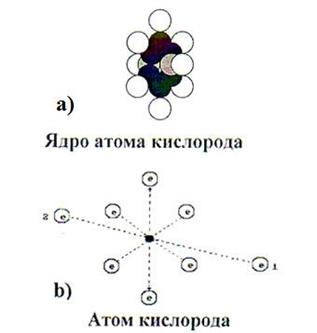
Рис. 49. Схемы ядра и атома кислорода
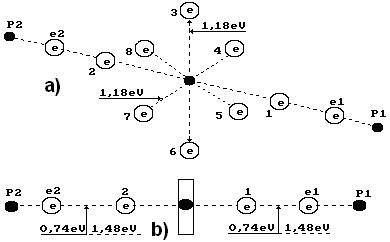
Рис. 50. Схема молекулы воды: 1,2,3,4,5,6,7,8 - номера электронов атома кислорода;
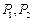 - ядра атомов водорода (протоны);
- ядра атомов водорода (протоны); 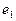 и
и 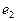 - номера электронов атомов водорода
- номера электронов атомов водорода
Два электрона 1 и 2 атома кислорода (рис. 49, b) расположены на оси атома, а шесть остальных – по кругу, перпендикулярному оси. Можно предположить, что суммарное электростатическое поле шести электронов, расположенных по кругу (назовем их кольцевыми электронами), удаляет первый и второй осевые электроны на большее расстояние от ядра атома, чем то расстояние от ядра атома, на котором распложены кольцевые электроны. Поэтому осевые электроны атома кислорода являются его главными валентными электронами. Именно к этим электронам и присоединяются электроны атомов водорода, и образуется молекула воды (рис. 50) [51].
Символами 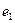 и
и 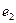 обозначены электроны атомов водорода, а символами
обозначены электроны атомов водорода, а символами 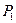 и
и 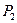 - протоны атомов водорода. Структура атома водорода (рис. 4) показывает, что если этот атом соединится с первым осевым электроном атома кислорода своим единственным электроном, то протон окажется на поверхности молекулы и образует зону с положительным зарядом, который будет генерироваться протоном атома водорода. Аналогичную зону сформирует и протон второго атома водорода, который соединяется со вторым осевым электроном атома кислорода (рис. 49). Отрицательно заряженную зону сформируют электроны атома кислорода, расположенные по кольцу вокруг оси атома кислорода [51].
- протоны атомов водорода. Структура атома водорода (рис. 4) показывает, что если этот атом соединится с первым осевым электроном атома кислорода своим единственным электроном, то протон окажется на поверхности молекулы и образует зону с положительным зарядом, который будет генерироваться протоном атома водорода. Аналогичную зону сформирует и протон второго атома водорода, который соединяется со вторым осевым электроном атома кислорода (рис. 49). Отрицательно заряженную зону сформируют электроны атома кислорода, расположенные по кольцу вокруг оси атома кислорода [51].
Поскольку при охлаждении электроны излучают фотоны и приближаются к ядру атома, то шесть кольцевых электронов атома кислорода в молекуле воды (рис. 50), приближаясь к ядру атома, своим статическим полем удаляют осевые электроны от ядра. В этом случае расстояние между атомами водорода, расположенными на оси молекулы воды, увеличиваются. Это главная причина увеличения размеров молекул воды при их замерзании.
Обратим внимание на то, что кластеры воды формируются, прежде всего, протон - протонными связями, когда две её молекулы соединяются соосно. Если учесть, что размер протона на три порядка меньше размера электрона, то протон – протонная связь легче разрушается при механическом воздействии на такой кластер (рис. 51, а). Второй вариант образования кластера – соединение осевого протона одной молекулы воды с кольцевым электроном другой молекулы воды. Это – протон – электронная связь (рис. 51, b). Её прочность тоже меньше прочности электрон - электронной связи. Эти факты и проясняют текучесть воды.
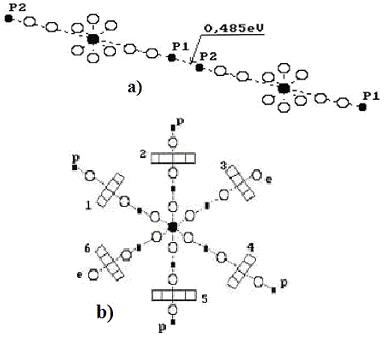
Рис. 51. Кластеры молекул воды: а) - линейный кластер воды;
b) шести лучевой кластер воды
Молекулы воды формируют кластеры различных форм. При определённых условиях и определённой температуре (в зимних облаках) шесть молекул воды присоединяются своими протонами атомов водорода к кольцевым электронам атома кислорода другой молекулы воды. В результате образуется шести лучевая структура, которая с увеличением размера и усложнением формирует ажурную шести лучевую структуру – снежинку. Этот естественный процесс реализуется при строго определённых энергиях связи валентных электронов, которые зависят от энергий поглощаемых и излучаемых фотонов.
Большое электрическое сопротивление воды обусловлено тем, что на осевых концах молекул располагаются положительно заряженные протоны атомов водорода. В результате линейные кластеры молекул воды имеют на обоих концах одноимённые заряды, что исключает возможность формирования электрической цепи в чистой воде.
Чтобы уменьшить электрическое сопротивление воды и увеличить её электропроводность, надо ввести в раствор ионы, которые имели бы на одном конце главной оси электрон, а на другом протон. В этом случае такие ионы легко объединяются в линейные кластеры с разными знаками электрических зарядов на их концах, что и приводит к формированию электрических цепей в растворе, которые увеличивают его электропроводность. В качестве примера можно рассмотреть присутствие в воде иона 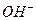 (рис. 52).
(рис. 52).
Известно, что вода может обладать щелочными или кислотными свойствами. Щелочные свойства формируются за счет увеличенного содержания в воде гидроксила 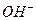 [1].
[1].
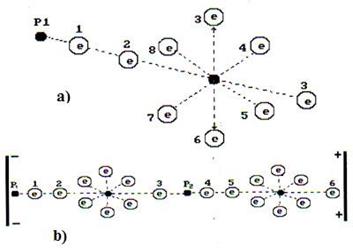
Рис. 52. Схемы: а) гидроксила 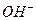 ; b) кластера
; b) кластера 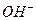
На рис. 52, а представлена схема гидроксила 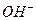 . На одном конце оси гидроксила расположен электрон атома кислорода, а другой - завершается протоном атома водорода. Таким образом, гидроксил – идеальное звено электрической цепи. Под действием приложенного напряжения эти ионы формируют линейные кластеры с положительным и отрицательным знаками электрических зарядов на концах (рис. 52, b). В результате электрический импульс напряжения передаётся вдоль этого кластера [1] .
. На одном конце оси гидроксила расположен электрон атома кислорода, а другой - завершается протоном атома водорода. Таким образом, гидроксил – идеальное звено электрической цепи. Под действием приложенного напряжения эти ионы формируют линейные кластеры с положительным и отрицательным знаками электрических зарядов на концах (рис. 52, b). В результате электрический импульс напряжения передаётся вдоль этого кластера [1] .
Конечно, ток не течёт вдоль кластера. Он формируется благодаря тому, что ион гидроксила 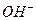 , расположенный на конце кластера у анода (рис. 52, b) отдаёт ему свой электрон, а протон атома водорода у иона
, расположенный на конце кластера у анода (рис. 52, b) отдаёт ему свой электрон, а протон атома водорода у иона 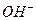 , расположенного у катода, получает электрон из сети.
, расположенного у катода, получает электрон из сети.
Если к этому добавить тот факт, что водород выделяется у катода (-), а кислород у анода, то факт движения электронов от анода (+) к катоду (-) во внешней цепи, соединяющей анод и катод, который мы уже описали, становится неоспоримым. На каком основании электротехники считают, что электроны в цепи постоянного тока движутся от минуса (-) к полюсу (+) остаётся тайной. Поэтому мы будем придерживаться уже описанного нами неоспоримого экспериментального факта о движении электронов в цепи постоянного тока от плюса (+) к минусу (-).
Известно, что молекулы водорода могут существовать в двух формах, которые называются ортоводородом и параводородом (рис. 53).
Итак, процесс электролиза начинается с выхода электрона 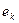 из катода в раствор. Осевые протоны
из катода в раствор. Осевые протоны 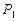 двух молекул воды (рис. 54, а и b), получив от катода по электрону
двух молекул воды (рис. 54, а и b), получив от катода по электрону 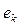 , соединяются в кластер, в структуре которого оказывается молекула ортоводорода (рис. 54, а) в синтезированном состоянии.
, соединяются в кластер, в структуре которого оказывается молекула ортоводорода (рис. 54, а) в синтезированном состоянии.
Рис. 53. Схема молекулы водорода 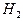 : а), b) - ортоводород; c) - параводород
: а), b) - ортоводород; c) - параводород
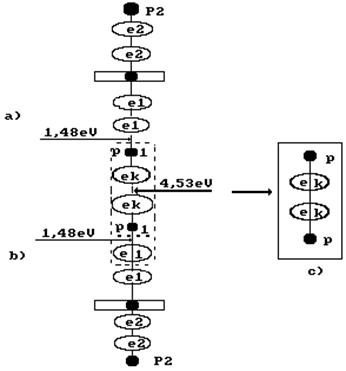
Рис. 54. Схема формирования молекулы ортоводорода в структуре кластера из двух
молекул воды
Теперь надо организовать такое импульсное воздействие на этот кластер, чтобы образовавшаяся молекула ортоводорода выделилась в свободное состояние (рис. 53, с). Обратим внимание на то, что на образование молекулы водорода в этом процессе расходуется два электрона 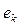 , пришедшие из катода, то есть из сети.
, пришедшие из катода, то есть из сети.
В соответствии с законом Фарадея, на образование одного моля водорода в этом случае расходуется два Фарадея Кулонов электричества 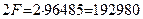 или
или 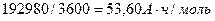 [1].
[1].
Если электролиз идет при напряжении 1,70V, то на получение одного моля водорода будет израсходовано 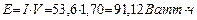 , а на получение
, а на получение 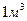 -
-
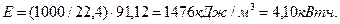 (66)
(66)
Как видно, расчеты с использованием закона Фарадея дают результат, совпадающий с расходом электроэнергии на получение одного кубического метра водорода из воды лучшими современными электролизёрами.
В Природе, например, при фотосинтезе, как мы уже отметили, этот показатель многократно меньше, поэтому перед нами естественный вопрос: как уменьшить затраты энергии но получение водорода из воды?
Для этого нам необходима информация об энергиях химических связей электронов атомов водорода и кислорода с их ядрами в момент пребывания электронов на любом энергетическом уровне (табл. 8 и 9).
В ряду энергий связей электрона с протоном атома водорода (табл. 8) и валентного электрона атома кислорода с протоном его ядра (табл. 9) есть энергии связи (1,51eV) и (1,53 eV), при которых начинается и идет процесс выделения газов в процессе электролиза воды, согласно старой теории этого процесса.
Эти энергии соответствуют пребыванию электронов на третьих энергетических уровнях. Раньше, из анализа процесса синтеза молекулы воды, мы установили, что энергия связи между электронами атомов водорода и кислорода в молекуле воды равна 1,48eV (рис. 50, b).
Таблица 8. Спектр атома водорода
| Значения | n | 2 | 3 | 4 | 5 | 6 |
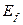 (эксп) (эксп)
| eV | 10,20 | 12,09 | 12,75 | 13,05 | 13,22 |
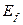 (теор) (теор)
| eV | 10,198 | 12,087 | 12,748 | 13,054 | 13,220 |
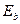 (теор) (теор)
| eV | 3,40 | 1,51 | 0,85 | 0,54 | 0,38 |
Таблица 9. Спектр первого электрона атома кислорода
| Значения | n | 2 | 3 | 4 | 5 | 6 |
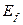 (эксп.) (эксп.)
| eV | 10,18 | 12,09 | 12,76 | 13,07 | 13,24 |
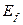 (теор.) (теор.)
| eV | 10,16 | 12,09 | 12,76 | 13,07 | 13,24 |
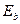 (теор.) (теор.)
| eV | 3,44 | 1,53 | 0,86 | 0,55 | 0,38 |
Итак, среди энергий связи электрона атома водорода с его ядром (протоном) есть энергия (1,51 eV), близкая к экспериментальному значению (1,48 eV). Определим аналогичные энергии для электронов атома кислорода.
Поскольку в химических реакциях участвуют, в основном, поверхностные электроны атомов, которые имеют близкие значения энергий связи с ядрами атомов на одноименных энергетических уровнях, то ограничимся анализом энергий связи первого электрона атома кислорода (табл. 9).
Как видно (табл. 9), энергии связи первого электрона атома кислорода практически совпадают с соответствующими энергиями связи электрона атома водорода (табл. 8). Причем, энергия, соответствующая третьему уровню (1,53 eV), близка к экспериментальному значению энергии (1,48 eV) газовыделения при низковольтном электролизе воды. Так что теоретические значения энергий связи электрона первого атома водорода и первого электрона атома кислорода в молекуле воды, полученные на основании закона формирования спектров, представленного в нашей монографии [1], близки к экспериментальным значениям этой энергии (табл. 9).
Теперь у нас появились веские основания полагать, что первый электрон атома кислорода, устанавливая связь с первым атомом водорода в молекуле воды, находится вблизи третьего ( 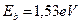 ) энергетического уровня (табл. 8).
) энергетического уровня (табл. 8).
Анализируя закономерность изменения энергий связи электронов атома кислорода и других атомов с их ядрами, мы установили, что в условиях присутствия в атоме всех электронов они имеют, примерно, одинаковые энергии связи с ядрами атомов. Поэтому будем считать, что симметричность молекулы воды обеспечивает равные (или близкие) энергии связи с ядром его первого и второго электронов.
Низковольтный процесс электролиза воды обычно идет при напряжении (1,6 - 2,3)B и достаточно большой силе тока, свидетельствующей о большом расходе электронов.
Поскольку первый и второй электроны атома кислорода удалены от его ядра дальше других электронов, то протон атома водорода, связанный с одним из этих электронов, первым приближается к катоду и получает от него электрон 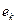 (рис. 54, а). После того, как две молекулы воды получат по электрону
(рис. 54, а). После того, как две молекулы воды получат по электрону 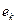 , их поверхностные электроны сразу же соединяются и образуют кластер из двух молекул воды (рис. 54, а, b), соединенных двумя электронами
, их поверхностные электроны сразу же соединяются и образуют кластер из двух молекул воды (рис. 54, а, b), соединенных двумя электронами 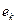 , испущенными катодом. Как видно, в цепочке протонов и электронов, соединяющих две молекулы воды, присутствует молекула ортоводорода (рис. 53, a и 54, а, b). Так как электроны, пришедшие от катода, прошли фазу свободного состояния, то синтез молекулы водорода в этой цепочке сопровождается затратами энергии, величину которой (на
, испущенными катодом. Как видно, в цепочке протонов и электронов, соединяющих две молекулы воды, присутствует молекула ортоводорода (рис. 53, a и 54, а, b). Так как электроны, пришедшие от катода, прошли фазу свободного состояния, то синтез молекулы водорода в этой цепочке сопровождается затратами энергии, величину которой (на 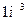 ) мы уже рассчитали (66).
) мы уже рассчитали (66).
Энергия синтеза одного моля молекул водорода равна 436кДж. Переведем её в электрон-вольты в расчете на одну молекулу [32].
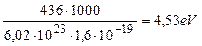 . (67)
. (67)
Величина этой энергии показана справа от молекулы водорода, расположенной в кластерной цепочке (рис. 54), а слева показаны энергии 1,48eV связи атомов водорода с атомами кислорода в молекулах воды. Энергия 4,53eV синтеза молекулы водорода перераспределяет энергии связи в кластерной цепочке таким образом, что энергии 1,48eV связи атомов водорода с атомами кислорода в молекулах воды становятся равными нулю и молекула ортоводорода выделяется из кластерной цепочки (рис. 54, с).
Таким образом, разность между энергией 4,53eV синтеза молекулы водорода и суммарной энергией связи (1,48+1,48) = 2,96 eV оказывается равной (4,53 – 2,96)=1,57eV. Эта энергия расходуется на нагревание электролитического раствора. Поэтому при выделении 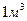 водорода выделится не 44,64х436=19463 кДж, предсказываемых старой теорией электролиза, а следующее количество тепловой энергии
водорода выделится не 44,64х436=19463 кДж, предсказываемых старой теорией электролиза, а следующее количество тепловой энергии
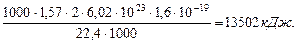 (68)
(68)
При этом у катода идёт химическая реакция
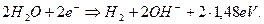 (69)
(69)
Вполне естественно, что количество тепловой энергии 13502кДж является частью общей энергии 4х3600 = 14400 кДж, расходуемой на получение одного кубического метра водорода [32]. Показатель тепловой эффективности этого процесса окажется таким
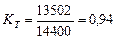 (70)
(70)
Важно иметь в виду, что энергию синтеза молекул кислорода мы не учли. Если же учитывать энергию синтеза молекул кислорода, то надо знать сколько кислорода выделятся при получении 1000 литров водорода. Известно, что из одного литра воды можно получить 1234,44 литра водорода и 604,69 литра кислорода. Тогда при выделении 1000 литров водорода выделится 60469/1234,4=489,86 литра кислорода. Учитывая, что энергия, выделяющаяся при синтезе одной молекулы кислорода, равна 4,95 eV (5,13 Кдж/моль), найдем количество энергии, которая выделится при синтезе 489,86 литров кислорода.
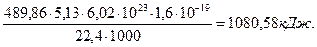 (71)
(71)
Тогда общий показатель тепловой эффективности будет равен
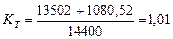 (72)
(72)
Таким образом, показатель общей тепловой эффективности (72) существующего низковольтного процесса электролиза воды близок к единице.
Если учесть, что энергосодержание одного грамма водорода равно 142 кДж, а кубический метр этого газа весит 90 гр., то показатель общей энергетической эффективности будет таким
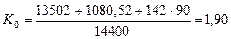 (73)
(73)
Рассмотрим теперь реакции, протекающие у анода (рис. 55). Известно, что ион гидроксила (рис. 55), имея отрицательный заряд 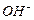 , движется к аноду (рис. 55, а). Два иона гидроксила, отдавая по одному электрону аноду и, соединяясь, друг с другом, образуют перекись водорода
, движется к аноду (рис. 55, а). Два иона гидроксила, отдавая по одному электрону аноду и, соединяясь, друг с другом, образуют перекись водорода 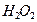 (рис. 55, b).
(рис. 55, b).
Известно также, что процесс образования перекиси водорода эндотермический, а молекулы кислорода - экзотермический. При получении одного кубического метра водорода процесс образования перекиси водорода поглощает 22,32х109,00=2432,88 кДж. В силу этого даже при плазмоэлектролитическом процессе температура раствора в зоне анода остаётся низкой.
Если бы существовал процесс синтеза молекул кислорода, то при получении одного кубического метра водорода в зоне анода выделилось бы 22,32х495,00=11048,40 кДж. Вычитая из этой величины энергию, поглощенную при синтезе перекиси водорода, получим 11048,40-2432,88=8615,52 кДж. Складывая эту энергию с энергией синтеза молекул водорода 19463,00 кДж, получим 28078,52 кДж. В этом случае общий показатель тепловой энергетической эффективности 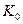 должен быть таким
должен быть таким 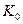 =28078,52/14400=1,95. Поскольку в реальности этой энергии нет, то этот факт подтверждает гипотезу об отсутствии процесса синтеза молекул водорода в зоне катода и молекул кислорода в зоне анода при низковольтном электролизе. Молекула водорода (рис. 55, c) и молекула кислорода (рис. 55, c) формируются в кластерных цепочках до выделения в свободное состояние, поэтому и не генерируется энергия их синтеза.
=28078,52/14400=1,95. Поскольку в реальности этой энергии нет, то этот факт подтверждает гипотезу об отсутствии процесса синтеза молекул водорода в зоне катода и молекул кислорода в зоне анода при низковольтном электролизе. Молекула водорода (рис. 55, c) и молекула кислорода (рис. 55, c) формируются в кластерных цепочках до выделения в свободное состояние, поэтому и не генерируется энергия их синтеза.
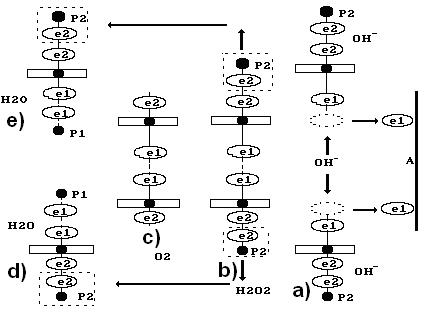
Рис. 55. Схемы: а) передача электронов 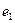 ионами
ионами 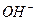 аноду А;
аноду А;
b) образование перекиси водорода 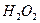 ;
;
с) образование молекулы кислорода 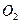 и двух молекул воды d) и e)
и двух молекул воды d) и e)
После передачи двумя ионами гидроксила двух электронов аноду (рис. 55, а) образуется молекула перекиси водорода 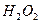 (рис. 55, b), которая, распадаясь, образует молекулу кислорода (рис. 55, с) и два атома водорода. Последние, соединяясь с ионами гидроксила, образуют две молекулы воды (рис. 55, d, e). С учетом этого химическая реакция в зоне анода запишется так
(рис. 55, b), которая, распадаясь, образует молекулу кислорода (рис. 55, с) и два атома водорода. Последние, соединяясь с ионами гидроксила, образуют две молекулы воды (рис. 55, d, e). С учетом этого химическая реакция в зоне анода запишется так
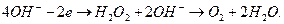 (74)
(74)
Итак, новая теория низковольтного электролиза воды устраняет противоречия старой теории и точнее отражает реальность.
Тут уместно привести точку зрения одного из наших читателей по поводу новой теории электролиза воды: «Филипп Михайлович, большое спасибо за статью "электролиз воды", из которой я узнал о воде больше, чем за всю свою долгую жизнь!!! Все очень четко, сжато, но понятно любому "чайнику", настоящий экстракт знаний! Еще раз - большое спасибо!!! С уважением, А.»
Теперь начнём искать пути реализации экономии электрической энергии, следующие из новой теории процесса электролиза воды. Для этого проанализируем результаты питания лабораторного электролизёра с помощью электронного генератора импульсов напряжения.
На рис. 56 показана осциллограмма напряжения при частоте импульсов около 200Гц. Масштаб записи один к одному. Импульсы не видны, так как их амплитуда ничтожно мала. Измерения показывают, что на осциллограмме зафиксировано напряжение около 13,5 Вольт. Вольтметр показывал в это время 11,4 Вольта.
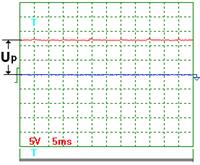 Рис. 56. Напряжение Рис. 56. Напряжение
| 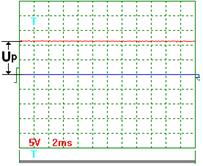 Рис. 57. Напряжение
Рис. 57. Напряжение
| 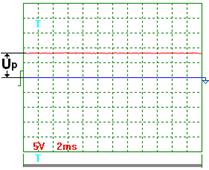 Рис. 58. Напряжение
Рис. 58. Напряжение
|
На рис. 56 показана осциллограмма напряжения на входе в электролизёр через 1 секунду после отключения его от сети. Как видно, электролизер имеет постоянную составляющую 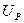 электрического потенциала. Через 3 секунды после отключения электролизёра от сети (рис. 58) потенциал на входе в электролизёр уменьшается с 11,4 В до 8 В, примерно. Осциллограммы на рис. 57 и 58 показывают, что после отключения электролизёра от сети идет процесс его разрядки. Это указывает на то, что электролизёр обладает свойствами конденсатора.
электрического потенциала. Через 3 секунды после отключения электролизёра от сети (рис. 58) потенциал на входе в электролизёр уменьшается с 11,4 В до 8 В, примерно. Осциллограммы на рис. 57 и 58 показывают, что после отключения электролизёра от сети идет процесс его разрядки. Это указывает на то, что электролизёр обладает свойствами конденсатора.
На осциллограмме (рис. 56) импульсы напряжения не видны, так как их амплитуда ничтожно мала. Если увеличить масштаб (записать с открытым входом), то импульсы напряжения выглядят так (рис. 59 и 60).
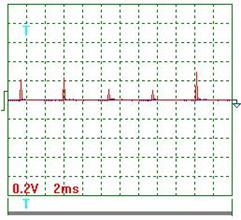 Рис. 59. Напряжение
Рис. 59. Напряжение
| 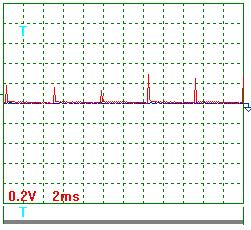 Рис. 60. Напряжение
Рис. 60. Напряжение
|
Ниже представлены результаты обработки осциллограмм напряжения (рис. 59 и 60). Учитывая масштабный коэффициент, равный 10, найдём среднее значение амплитуды импульсов напряжения
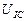 =[(0,20+0,24+0,12+0,10+0,30+0,18+0,16+0,12+0,30+ +0,24+0,30)/11] x10=2,05 В.
=[(0,20+0,24+0,12+0,10+0,30+0,18+0,16+0,12+0,30+ +0,24+0,30)/11] x10=2,05 В.
Период импульсов Т=(24х2)/10=4,8 мс.
Длительность импульсов 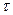 =(2х1,45)/10=0,29мс.
=(2х1,45)/10=0,29мс.
Частота импульсов 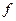 =(1/0,001x4,8)=208,3 Гц.
=(1/0,001x4,8)=208,3 Гц.
Скважность импульсов 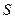 =4,8/0,29=16,55.
=4,8/0,29=16,55.
Коэффициент заполнения 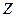 =0,5/16,55=0,0302
=0,5/16,55=0,0302
Таким образом, есть основания полагать, что электролизёр обладает свойствами конденсатора и источника электричества одновременно. Зарядившись в начале, он постепенно разряжается под действием электролитических процессов, протекающих в нём. Количество генерируемой им электрической энергии оказывается недостаточным, чтобы поддерживать процесс электролиза, и он постепенно разряжается. Если его подзаряжать импульсами напряжения, компенсирующими расход энергии, то заряд электролизёра, как конденсатора, будет оставаться постоянным, а процесс электролиза - стабильным.
Величина среднего напряжения, необходимого для компенсации разрядки электролизёра, зафиксирована на осциллограммах рис. 63 и 65. Она равна 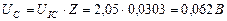 . Вольтметр в это время показывал полное напряжение на клеммах электролизёра, равное 11,4 В.
. Вольтметр в это время показывал полное напряжение на клеммах электролизёра, равное 11,4 В.
На рис. 61 и 62 показаны осциллограммы тока, когда источник питания электролизёра генерировал импульсы с частотой около 200Гц. Результаты обработки этих осциллограмм следующие.
Учитывая масштабный коэффициент, равный 10, и сопротивление резистора 0,10 Ом, найдём среднее значение амплитуды импульсов тока.
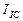 ={[(9,0+7,0+2,0+11,5+6,0+8,5+3,5+9,0+2,5+6,5)/10]x10}/0,10=0,66 А. Средний ток в цепи питания электролизёра
={[(9,0+7,0+2,0+11,5+6,0+8,5+3,5+9,0+2,5+6,5)/10]x10}/0,10=0,66 А. Средний ток в цепи питания электролизёра 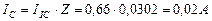 . Эту же величину (0,02А) показывал и амперметр.
. Эту же величину (0,02А) показывал и амперметр.
Таким образом, получается две величины мощности на клеммах электролизёра. Первая, которая до сих пор учитывалась всеми, равна произведению напряжения на клеммах электролизёра (11,40 В) на среднюю величину тока (0,02А), то есть 11,40х0,02=0,23 Ватта.
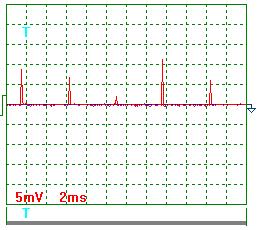 Рис. 61. Ток
Рис. 61. Ток
| 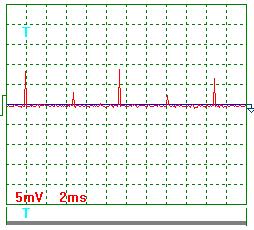 Рис. 62. Ток
Рис. 62. Ток
|
Сразу возникает вопрос: какое отношение имеет напряжение на клеммах электролизёра (11,40 В) к расходу энергии на процесс электролиза воды? Ведь оно принадлежит электролизёру, но не источнику питания. Электронный генератор импульсов подавал электролизёру импульсы напряжения (рис. 59, 60), амплитуда которых близка к величине напряжения на клеммах электролизёра. Поэтому для расчёта мощности, расходуемой на питание электролизёра, надо брать среднюю величину импульсов напряжения, также учитывающую их скважность 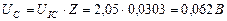 и среднюю величину тока, равную
и среднюю величину тока, равную 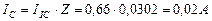 . Тогда реальный расход мощности на подзарядку электролизёра будет равен
. Тогда реальный расход мощности на подзарядку электролизёра будет равен 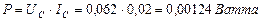 , а не 0,23 Ватта, как считалось до сих пор. Сразу возникает вопрос: как доказать связь с реальностью описанных противоречий? Чтобы найти ответ на этот вопрос, проанализируем процесс питания электролизёра детальнее.
, а не 0,23 Ватта, как считалось до сих пор. Сразу возникает вопрос: как доказать связь с реальностью описанных противоречий? Чтобы найти ответ на этот вопрос, проанализируем процесс питания электролизёра детальнее.
5.3. Анализ процесса питания электролизёра
Электролизёр – это совокупность пластинчатых анодов и катодов, каждая пара которых называется ячейкой. Раствор размещается между пластинами электродов. Напряжение на клеммы электролизёра можно подавать непрерывно, а можно импульсами. Мы уже увидели потенциальные возможности импульсного процесса подачи напряжения на клеммы электролизёра в снижении затрат энергии на его работу. Теперь надо выяснить, как реализовать эту возможность?
Мы уже показали, что все электролизёры, заряжаясь в начале работы, приобретают постоянный потенциал 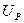 , свойственный конденсатору. Величина этого потенциала увеличивается с увеличением количества ячеек в электролизёре (рис. 63).
, свойственный конденсатору. Величина этого потенциала увеличивается с увеличением количества ячеек в электролизёре (рис. 63).
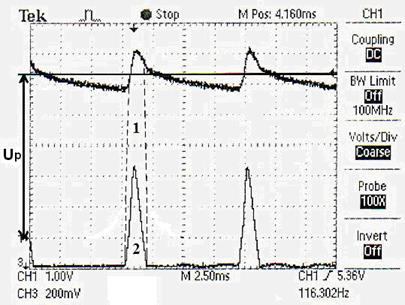
Рис. 63. Осциллограмма напряжения и тока питания электролизёра:
1 – импульс напряжения; 2 – импульс тока; 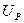 - средняя величина постоянного потенциала
- средняя величина постоянного потенциала
Поскольку электрическая сеть электролизёра связана со всей электрической сетью, то приборы, измеряющие мощность, потребляемую электролизёром, формируют показания, в которых учитывается величина постоянного потенциала 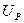 , принадлежащая электролизёру, и средняя величина, формирующегося при этом импульсного электрического тока.
, принадлежащая электролизёру, и средняя величина, формирующегося при этом импульсного электрического тока.
На рис. 63 хорошо видно, что импульсы напряжения восстанавливают средний потенциал 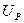 электролизера, который уменьшается при отсутствии импульса. Это значит, что нет нужды подавать напряжение в электролизёр непрерывно, так как он имеет свой потенциал, для поддержания заданной величины которого достаточна периодическая подзарядка электролизёра.
электролизера, который уменьшается при отсутствии импульса. Это значит, что нет нужды подавать напряжение в электролизёр непрерывно, так как он имеет свой потенциал, для поддержания заданной величины которого достаточна периодическая подзарядка электролизёра.
При такой системе подачи электрической энергии в электролизёр измерительные приборы учитывают не величину напряжения, которое необходимо для его подзарядки, а полную величину постоянного потенциала 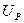 , которая, вполне естественно, больше средней величины амплитуды напряжения, необходимого для подзарядки электролизёра. Так работают все современные электролизёры, и все варианты совершенствования такого способа его питания уже задействованы. Из изложенного следует, что реальная энергия, затрачиваемая на процесс электролиза воды, меньше той, которую показывают приборы. Как определить её величину?
, которая, вполне естественно, больше средней величины амплитуды напряжения, необходимого для подзарядки электролизёра. Так работают все современные электролизёры, и все варианты совершенствования такого способа его питания уже задействованы. Из изложенного следует, что реальная энергия, затрачиваемая на процесс электролиза воды, меньше той, которую показывают приборы. Как определить её величину?
Электронный ключ 3 (рис. 64) генерирует импульсы напряжения, разрывая электрическую цепь и нарушая связь постоянного потенциала электролизёра 1 с постоянным потенциалом аккумулятора 2.
Показания вольтметров следующие: 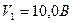 ;
; 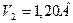 ;
; 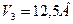 . Показания амперметра
. Показания амперметра 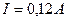 . В результате, в каждом сечении цепи питания - своя мощность:
. В результате, в каждом сечении цепи питания - своя мощность:
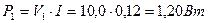 ; (75)
; (75)
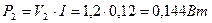 ; (76)
; (76)
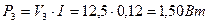 . (77)
. (77)

Рис. 64. Схема импульсного питания электролизёра 1
от аккумуляторной батареи 2 через диод 4
Возникает вопрос: какую же мощность реализует аккумулятор для питания электролизёра? Для получения ответа на этот вопрос проанализируем осциллограммы напряжений и токов, представленные на рис. 65, 66 и 67.
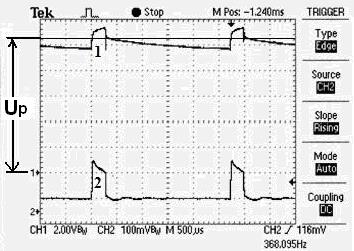
Рис. 65. Осциллограммы напряжения и тока на клеммах электролизёра 1 (рис. 64)
Как видно (рис. 64, 65), величина импульсов напряжения (1) больше величины постоянного потенциала 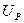 электролизёра. Импульсы восстанавливают его до средней величины, после чего напряжение вновь уменьшается. Следующий импульс восстанавливает напряжение электролизера до средней величины. При этом импульсы тока (2) генерируются синхронно с импульсами напряжения.
электролизёра. Импульсы восстанавливают его до средней величины, после чего напряжение вновь уменьшается. Следующий импульс восстанавливает напряжение электролизера до средней величины. При этом импульсы тока (2) генерируются синхронно с импульсами напряжения.
На рис. 66 эти импульсы представлены без постоянного потенциала электролизёра и их мощность определить легко.
Амплитуда импульса напряжения (рис. 66) равна 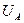 =12,5 V, а амплитуда импульса тока –
=12,5 V, а амплитуда импульса тока – 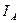 =1,30 А (рис. 66). Скважность импульсов равна
=1,30 А (рис. 66). Скважность импульсов равна 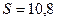 . Тогда старый закон (32) формирования средней величины импульсной электрической мощности даёт такой результат
. Тогда старый закон (32) формирования средней величины импульсной электрической мощности даёт такой результат
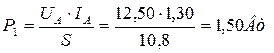 . (78)
. (78)
Эта величина близка к показаниям приборов, установленных перед электролизёром (75).
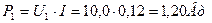 (79)
(79)
и совпадает с величиной мощности на клеммах аккумулятора (77)
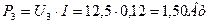 . (80)
. (80)
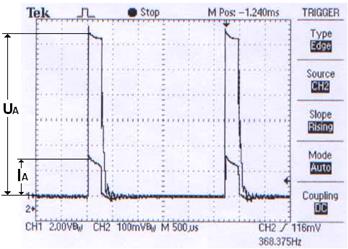
Рис. 66. Осциллограммы напряжения и тока перед диодом 4 (рис. 64)
На рис. 67 видно, что напряжение аккумулятора не реагирует на импульсы напряжения, а величина тока на пути от электролизёра 1 (рис. 64) до аккумулятора 2 остаётся почти неизменной (рис. 65, 66, 67).
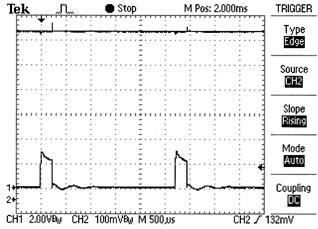
Рис. 67. Осциллограмма напряжения и тока на клеммах аккумулятора 2 (рис. 64)
В опыте использовался мини электролизёр с производительностью 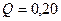 литра водорода в час. С учетом показаний разных приборов и результатов, представленных в формулах (75), (76) и (77), удельная мощность составляла:
литра водорода в час. С учетом показаний разных приборов и результатов, представленных в формулах (75), (76) и (77), удельная мощность составляла:
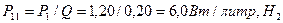 ; (81)
; (81)
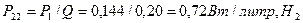 ; (82)
; (82)
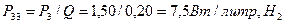 . (83)
. (83)
Вполне естественно, что общий ток 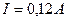 и разные напряжения в разных сечениях электрической цепи формируют разную мощность, и возникает вопрос: какая мощность расходуется на питание электролизера?
и разные напряжения в разных сечениях электрической цепи формируют разную мощность, и возникает вопрос: какая мощность расходуется на питание электролизера?
Средняя величина тока 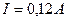 , которую показывает амперметр, равна импульсной величине 1,3 А, деленной на скважность импульсов
, которую показывает амперметр, равна импульсной величине 1,3 А, деленной на скважность импульсов 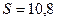 (
( 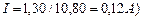 . Поэтому вполне естественно, что на клеммах электролизёра мощность равна
. Поэтому вполне естественно, что на клеммах электролизёра мощность равна 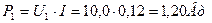 . На клеммах аккумулятора она несколько больше
. На клеммах аккумулятора она несколько больше 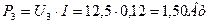 .
.
Имеем ли мы право определять мощность 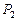 (76) на клеммах диода, умножая среднюю величину тока
(76) на клеммах диода, умножая среднюю величину тока 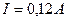 на амплитудное значение импульса напряжения, равное
на амплитудное значение импульса напряжения, равное 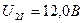 ? Ведь напряжение подаётся не постоянно, а импульсами, поэтому мы импульсное значение напряжения также должны разделить на скважность
? Ведь напряжение подаётся не постоянно, а импульсами, поэтому мы импульсное значение напряжения также должны разделить на скважность 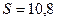 . В результате будем иметь среднюю величину напряжения
. В результате будем иметь среднюю величину напряжения 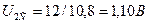 . Это близко к показаниям вольтметра
. Это близко к показаниям вольтметра 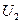 . В результате получим
. В результате получим
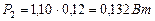 (84)
(84)
или на один литр водорода
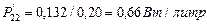 . (85)
. (85)
Вводим в цепь питания электронный генератор импульсов. Результаты эксперимента представлены в табл. 10. Частота импульсов составляла  350 Гц, а скважности импульсов S = 1; 5; 10. Электролизёр имел 6 мини ячеек.
350 Гц, а скважности импульсов S = 1; 5; 10. Электролизёр имел 6 мини ячеек.
Таблица 10. Показатели электролиза согласно показаниям приборов на рис. 64
| 0.Показатели | S=1 | S=5 | S=10 |
1. Получено 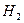 , л/ч , л/ч
| 0,55 | 0,16 | 0,14 |
| 2. Ток, А | 0,23 | 0,12 | 0,11 |
3.Напряж. 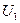
| 12,40 | 11,00 | 10,10 |
4.Напряж. 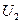
| 12,50 | 2,50 | 1,20 |
5.Напряж. 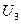
| 12,50 | 12,50 | 12,50 |
6.Мощ., 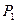
| 2,87 | 1,32 | 1,11 |
7.Мощ., 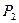
| 2,87 | 0,30 | 0,13 |
8.Мощ., 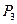
| 2,87 | 1,50 | 1,37 |
9. Уд. мощ., 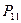 , Вт/л , Вт/л
| 5,22 | 8,25 | 7,93 |
10. Уд. мощ., 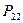 , Вт/л , Вт/л
| 5,22 | 1,87 | 0,93 |
11. Уд. мощ., 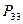 , Вт/л , Вт/л
| 5,22 | 9,37 | 9,78 |
Обратим внимание на то, что при увеличении скважности в 10 раз (S=10) производительность электролизёра уменьшилась в 4 раза. Удельные затраты мощности 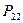 по показаниям приборов перед диодом также уменьшились в 5,6 раза.
по показаниям приборов перед диодом также уменьшились в 5,6 раза.
Нетрудно видеть (рис. 65, 67 и табл. 10, 11), что удельная мощность 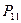 включает в себя постоянный потенциал электролизера и не отражает истинные затраты энергии на электролиз воды. С увеличением скважности импульсов уменьшается ток и падает производительность, а напряжение остаётся почти постоянным и равным напряжению на клеммах аккумулятора (
включает в себя постоянный потенциал электролизера и не отражает истинные затраты энергии на электролиз воды. С увеличением скважности импульсов уменьшается ток и падает производительность, а напряжение остаётся почти постоянным и равным напряжению на клеммах аккумулятора ( 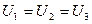 ), что и увеличивает удельный расход мощности
), что и увеличивает удельный расход мощности 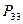 .
.
Если напряжение подаётся импульсами (рис. 66), то среднее напряжение импульсов, показываемое вольтметром 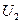 (рис. 65) уже не равно напряжению постоянного потенциала электролизера и напряжению на клеммах аккумулятора. Средняя величина этого напряжения
(рис. 65) уже не равно напряжению постоянного потенциала электролизера и напряжению на клеммах аккумулятора. Средняя величина этого напряжения 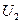 равна амплитуде импульсов напряжения, делённой на скважность (
равна амплитуде импульсов напряжения, делённой на скважность ( 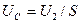 ). Поскольку ток в цепи один, то мощность импульсов равна произведению тока на среднее значение напряжения
). Поскольку ток в цепи один, то мощность импульсов равна произведению тока на среднее значение напряжения 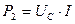 .
.
Однако, нагрузка на клеммах аккумулятора определяется не средним значением импульсного напряжения 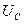 , а его постоянной величиной
, а его постоянной величиной 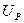 . Из этого следует ошибочность расхода энергии аккумулятором путём подачи энергии импульсами. Мощность
. Из этого следует ошибочность расхода энергии аккумулятором путём подачи энергии импульсами. Мощность 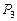 , реализуемая аккумулятором (77) всегда равна произведению тока на среднюю величину импульса напряжения.
, реализуемая аккумулятором (77) всегда равна произведению тока на среднюю величину импульса напряжения.
Как видно (табл. 10), с увеличением скважности импульсов в десять раз производительность уменьшается в четыре раза, а мощность на клеммах электролизёра 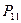 и на клеммах аккумулятора
и на клеммах аккумулятора 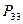 увеличивается. Из этого следует, что при уменьшении интенсивности процесса электролиза воды расход энергии на этот процесс растёт. Вряд ли с этим можно согласиться. Удельный расход не может так резко увеличиваться. Он должен оставаться, примерно, одинаковым. А получаемое увеличение расхода энергии – следствие искажённых показаний приборов. Возникает вопрос: какие из них отражают реальность?
увеличивается. Из этого следует, что при уменьшении интенсивности процесса электролиза воды расход энергии на этот процесс растёт. Вряд ли с этим можно согласиться. Удельный расход не может так резко увеличиваться. Он должен оставаться, примерно, одинаковым. А получаемое увеличение расхода энергии – следствие искажённых показаний приборов. Возникает вопрос: какие из них отражают реальность?
Таблица 11. Влияние скважности импульсов на показатели процесса электролиза воды
| 0.Показатели | S=1 | S=2 | S=3 | S=4 | S=5 | S=10 |
| 1. Н2, л/ч | 0,63 | 0,57 | 0,52 | 0,48 | 0,44 | 0,33 |
| 2.Ток пост., А | 0,25 | 0,24 | 0,22 | 0,22 | 0,20 | 0,20 |
| 3.Ток имп., А | 0,25 | 0,45 | 0,65 | 0,85 | 1,00 | 2,00 |
| 4.Напряж.U1,В | 12,50 | 12,26 | 11,94 | 11,85 | 11,59 | 10,78 |
| 5 Напряж.U2,В | 12,50 | 6,30 | 4,20 | 3,20 | 2,50 | 1,30 |
| 6 Напряж.U3,В | 12,50 | 12,50 | 12,50 | 12,50 | 12,50 | 12,50 |
| 7.Мощн., Р1 | 3,13 | 2,94 | 2,63 | 2,61 | 2,32 | 2,16 |
| 8.Мощн., Р2 | 3,12 | 1,51 | 0,92 | 0,70 | 0,50 | 0,26 |
| 9.Мощн., Р3 | 3,13 | 3,00 | 2,75 | 2,75 | 2,50 | 2,50 |
| 10.Удел. мощ., Р11, Вт/л | 4,97 | 5,16 | 5,06 | 5,44 | 5,27 | 6,55 |
| 11.Удел. мощ., Р22, Вт/л | 4,95 | 2,65 | 1,77 | 1,46 | 1,14 | 0,79 |
| 12.Удел. мощ., Р33, Вт/л | 4,97 | 5,26 | 5,29 | 5,73 | 5,68 | 7,58 |
Изложенное показывает, что величины удельной мощности на клеммах электролизёра 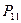 и на клеммах аккумулятора
и на клеммах аккумулятора 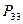 явно не отражают реальность (табл. 10, 11). Поэтому надо уделить внимание анализу удельной мощности
явно не отражают реальность (табл. 10, 11). Поэтому надо уделить внимание анализу удельной мощности 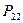 на клеммах диода. Если удельный расход энергии – величина почти постоянная, то производительность электролизёра при увеличении скважности импульсов в 10 раз должна уменьшиться также, примерно, в 10 раз, но она уменьшилась лишь в 4 раза (табл. 10) и в 2 раза (табл. 11). Это означает, что прекращение подачи напряжения не останавливает процесс электролиза воды. Он продолжается за счёт постоянного потенциала
на клеммах диода. Если удельный расход энергии – величина почти постоянная, то производительность электролизёра при увеличении скважности импульсов в 10 раз должна уменьшиться также, примерно, в 10 раз, но она уменьшилась лишь в 4 раза (табл. 10) и в 2 раза (табл. 11). Это означает, что прекращение подачи напряжения не останавливает процесс электролиза воды. Он продолжается за счёт постоянного потенциала 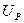 . Уменьшение его величины, зафиксированное на осциллограммах (рис. 56, 57), подтверждает это.
. Уменьшение его величины, зафиксированное на осциллограммах (рис. 56, 57), подтверждает это.
Сравнивая осциллограммы на рис. 60 и 62, видим, что вольтметр, подключённый к клеммам электролизёра всегда будет показывать его полное напряжение, равное полному потенциалу 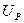 электролизёра. Фактическое же среднее напряжение
электролизёра. Фактическое же среднее напряжение 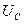 на клеммах электролизёра всегда меньше. Оно равно амплитуде импульса напряжения
на клеммах электролизёра всегда меньше. Оно равно амплитуде импульса напряжения 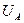 , делённой на скважность импульсов
, делённой на скважность импульсов 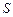 .
.
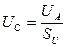 . (86)
. (86)
Вполне естественно, что средняя величина тока 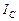 определится по аналогичной формуле
определится по аналогичной формуле
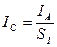 . (87)
. (87)
Так как  , то для работы электролизёра достаточно мощности
, то для работы электролизёра достаточно мощности
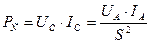 . (88)
. (88)
Однако, вольтметр, подключённый к клеммам электролизёра, покажет другую величину напряжения. Она будет равна 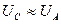 и мы получим среднюю мощность на клеммах электролизёра, определённую по ошибочной формуле (32).
и мы получим среднюю мощность на клеммах электролизёра, определённую по ошибочной формуле (32).
В результате величина мощности, необходимой электролизёру, для подзарядки его постоянного потенциала, окажется увеличенной в количество раз, равное скважности импульсов  и мы не получим никакой экономии электроэнергии. Вместе с тем мы явно видим наличие возможности для экономии и уже знаем, как это сделать.
и мы не получим никакой экономии электроэнергии. Вместе с тем мы явно видим наличие возможности для экономии и уже знаем, как это сделать.
Сейчас покажем, что этот эффект реализуется при питании электролизера с помощью электромеханического генератора импульсов (ЭМГИ). Поскольку промышленность ещё не выпускает такие генераторы, то мы переоборудовали серийный электромотор Axi 2826/12 в электромеханический генератор импульсов (ЭМГИ), оставив на его роторе два постоянных магнита.
Экспериментально установлено, что если ЭМГИ подаёт в электролизер импульсы напряжения 1, амплитуда которых больше постоянного электрического потенциала 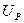 электролизёра, то этих импульсов достаточно для подзарядки электролизёра (рис. 63, 65).
электролизёра, то этих импульсов достаточно для подзарядки электролизёра (рис. 63, 65).
Вполне естественно, что нагрузка на валу ЭМГИ будет присутствовать только в моменты времени, когда генерируются импульсы напряжения и тока, средние величины которых определяются по формулам (86) и (87). Средняя мощность на валу ЭМГИ будет равна величине, определённой по формуле (88) и сложенной с мощностью 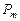 , расходуемой на механические потери на привод ЭМГИ, которые многократно меньше мощности, расходуемой на генерацию импульсов напряжения
, расходуемой на механические потери на привод ЭМГИ, которые многократно меньше мощности, расходуемой на генерацию импульсов напряжения 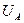 и тока
и тока 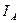 . В результате мощность, необходимая для работы электролизёра определятся по формуле
. В результате мощность, необходимая для работы электролизёра определятся по формуле
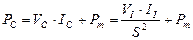 . (89)
. (89)
Самым удивительным является то, что абсолютное большинство электриков и электронщиков, с которыми нам пришлось обсуждать изложенное, не понимают его суть и считают, что не может быть в этом случае никакой экономии электрической энергии, так как её наличие сразу нарушает законы Кирхгофа. Посмотрим, так это или нет.
Первый закон или первое правило Кирхгофа формулируется так [52]: сумма всех токов, притекающих к любой точке цепи, равна сумме всех токов, утекающих от этой точки. Нетрудно видеть, что это правило строго реализуется в математической модели (32), если полагать, что процедура деления на скважность 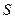 импульса в формуле (32) относится только к току и не относится к напряжению. В этом случае во всех сечениях электрической цепи первое правило Кирхгофа работает.
импульса в формуле (32) относится только к току и не относится к напряжению. В этом случае во всех сечениях электрической цепи первое правило Кирхгофа работает.
Второй закон или второе правило Кирхгофа гласит, что в замкнутой электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на отдельных участках цепи.
А теперь присмотримся к рис. 63 и 65. На них показано по два электрических потенциала. Один средний 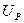 принадлежит самому электролизёру и его величина изменяется незначительно. Второй импульсный потенциал 1 с амплитудой близкой к максимальной величине потенциала электролизёра. Сразу возникает вопрос: какой потенциал мы должны учитывать для проверки достоверности второго закона Кирхгофа?
принадлежит самому электролизёру и его величина изменяется незначительно. Второй импульсный потенциал 1 с амплитудой близкой к максимальной величине потенциала электролизёра. Сразу возникает вопрос: какой потенциал мы должны учитывать для проверки достоверности второго закона Кирхгофа?
Средний потенциал 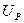 принадлежит электролизёру, который мы подзаряжаем, посылая импульсы напряжения (рис. 63, 65 и 66), поэтому
принадлежит электролизёру, который мы подзаряжаем, посылая импульсы напряжения (рис. 63, 65 и 66), поэтому 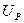 не имеет никакого отношения к расходу энергии на процесс электролиза воды. Вполне естественно, что мы обязаны в этом случае учитывать среднюю величину импульсов напряжения, которая равна амплитуде импульса напряжения, делённой на скважность импульсов
не имеет никакого отношения к расходу энергии на процесс электролиза воды. Вполне естественно, что мы обязаны в этом случае учитывать среднюю величину импульсов напряжения, которая равна амплитуде импульса напряжения, делённой на скважность импульсов 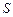 , как это и представлено в формуле (86).
, как это и представлено в формуле (86).
Поскольку средний потенциал 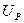 на клеммах электролизёра (рис. 63 и 65) больше среднего потенциала
на клеммах электролизёра (рис. 63 и 65) больше среднего потенциала  , подзаряжающего его, в количество раз, равное скважности импульсов, то и результаты реализации 2-го закона Кирхгофа в этих случаях будут отличаться в количество раз, равное скважности импульсов напряжения.
, подзаряжающего его, в количество раз, равное скважности импульсов, то и результаты реализации 2-го закона Кирхгофа в этих случаях будут отличаться в количество раз, равное скважности импульсов напряжения.
Итак, мы имеем явное нарушение второго закона Кирхгофа. Почему это не заметили все наши предшественники? Потому, что первичный источник питания, из которого выделяются импульсы напряжения, генерирует напряжение непрерывно и средний ток, пришедший к его клеммам, умножением на величину непрерывно генерируемого напряжения  , а на среднюю величину, определённую по формуле (86). В результате второй закон Кирхгофа казалось достоверным. Чтобы убедиться в этом, мы использовали в качестве источника питания электромеханический генератор электрических импульсов (ЭМГИ). Тогда среднее импульсное напряжение на клеммах первичного источника питания и на клеммах электролизёра оказывалось одинаковое и мы имели право рассчитывать мощность на клеммах такого источника питания по формуле (31).
, а на среднюю величину, определённую по формуле (86). В результате второй закон Кирхгофа казалось достоверным. Чтобы убедиться в этом, мы использовали в качестве источника питания электромеханический генератор электрических импульсов (ЭМГИ). Тогда среднее импульсное напряжение на клеммах первичного источника питания и на клеммах электролизёра оказывалось одинаковое и мы имели право рассчитывать мощность на клеммах такого источника питания по формуле (31).
На рис. 68 показана схема соединения импульсного источника питания (ЭГМИ) и измерительных приборов. При проведении эксперимента в качестве ячеек использованы электроды из нержавеющей стали газогенератора «Аква – Терм», изготовляемого Азовским ПО «Донпрессмаш».
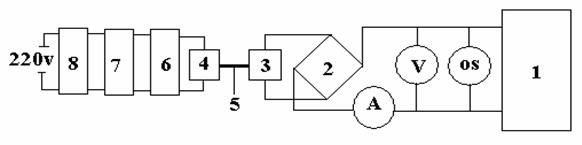
Рис. 68. Схема питания электролизёра: 1 – электролизёр; 2 – выпрямитель;
3 – ЭМГИ; 4 – электромотор; 5 – единый вал ЭМГИ 3 и электромотора 4;
6 – ваттметр PX – 110; 7 – ЛАТР; 8 – счетчик электроэнергии СО – И446М;
А – амперметр М-2015; V – вольтметр М-2004; OS – осциллограф TDS 2014.
Затраты энергии на получение водорода из воды при использовании электромеханического генератора электрических импульсов зависят от амплитуды импульсов тока и их скважности (табл. 12 и 13).
Таблица 12. Показатели эффективности экспериментального электролизёра, питаемого ЭМГИ
| Показатели | 1 |
1. Скважность импульсов напряжения 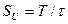
| 2,70 |
2. Скважность импульсов тока 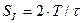
| 5,40 |
3. Расход воды 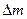 , гр./час , гр./час
| 0,73 |
4. Получение водорода 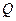 , л/час , л/час
| 0,99 |
| 5. Вольтметр U, В | 2,03 |
| 6. Амперметр I, А | 2,00 |
7. Мощность 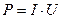 , Ватт , Ватт
| 4,06 |
8. Амплитуда импульса напряжения по осцил. 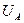 , В , В
| 1,90 |
9. Амплитуда импульса тока по осцил. 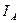 , А , А
| 10,00 |
10. Среднее напряжение по осцил. 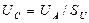 , В , В
| 0,70 |
11. Средний ток по осциллограмме 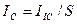 , А , А
| 1,80 |
12. Средняя мощность по осцил. 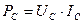 Ватт Ватт
| 1,27 |
13. Удельная мощность по осцил 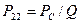 , Вт.ч./л , Вт.ч./л 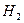
| 1,28 |
14. Мощность по счетчику электроэнергии 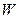 , Вт , Вт
| 0,70 |
15. Удельная мощность по счетчику электроэнергии, 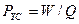 Вт.ч/литр Вт.ч/литр 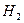
| 0,71 |
Примечание: один опыт – среднее 3-х повторностей.
Переоборудованный электродвигатель Axi 2826/12 использовался как генератор импульсов (ЭМГИ), приводимый во вращение стандартным Axi 2826/12. Он генерировал треугольные импульсы напряжения, которые подавались в экспериментальную ячейку электролизёра. Результаты эксперимента представлены в табл. 12 и 13.
Длительность прямоугольных импульсов напряжения и треугольных импульсов тока (рис. 69) одинакова. Специалист легко может установить, что период следования импульсов равен 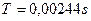 , длительность импульсов
, длительность импульсов 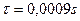 .
.
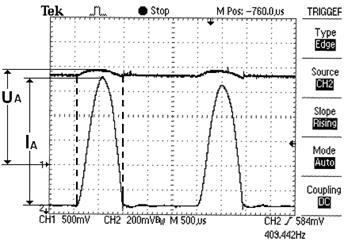
Рис. 69. Осциллограмма напряжения и тока на клеммах экспериментального
электролизёра
Поскольку форма импульсов напряжения, генерируемых генератором, - прямоугольная, то скважность импульсов 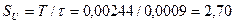 . Средняя величина напряжения оказывается такой
. Средняя величина напряжения оказывается такой 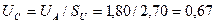 В. Форма импульсов тока близка к треугольной, поэтому их скважность в два раза больше
В. Форма импульсов тока близка к треугольной, поэтому их скважность в два раза больше 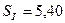 и средняя величина тока
и средняя величина тока 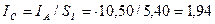 А. Вполне естественно, что средняя мощность на валу генератора импульсов будет равна
А. Вполне естественно, что средняя мощность на валу генератора импульсов будет равна
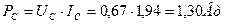 . (90)
. (90)
или
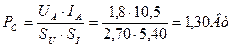 . (91)
. (91)
Как видно (табл. 12), эта величина 1,30Вт близка к показаниям осциллографа (табл. 12, пункт 12) и показаниям счётчика электроэнергии (табл. 12, пункт 14).
Итак, результаты эксперимента, представленные в табл. 10, убедительно доказывают необходимость определения амплитудных значений напряжения и тока путём деления их на свою скважность импульсов и рассчитывать среднюю величину импульсной мощности по формуле (31), а ошибочный второй закон Кирхгофа требует рассчитывать среднюю импульсную мощность на питание электролизёра по формуле (32), содержащей одну скважность. Сразу возникает вопрос: какую же скважность импульсов надо использовать в этом случае? Скважность импульсов напряжения или тока? Ответа нет. В связи с этим ошибочно также и представление о том, что однократное деление на скважность импульсов при определении мощности по формуле (32) обусловлено тем, что импульсы напряжения и тока (рис. 63, 66, 67) изменяются синхронно.
Конечно, весьма желательно проверить влияние большой скважности импульсов напряжения и тока на эффективность процесса электролиза воды. Но у нас не было электромеханического генератора импульсов с большей скважностью. Тем не менее, если не менять метод обработки осциллограмм, то это можно проверить и с помощью электронного генератора импульсов. Результаты такой проверки представлены в табл. 13.
Таблица 13. Показатели эффективности трёх ячеек серийного электролизёра «Аква-Терм» при использовании электронного генератора электрических импульсов
| Показатели | 1 | 2 | 3 |
1. Скважность импульсов 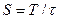
| 188 | 185 | 220 |
2. Расход воды  , гр./час , гр./час
| 0,87 | 1,12 | 1,36 |
3. Получение водорода 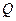 , л/час , л/час
| 1,19 | 1,53 | 1,86 |
| 4. Вольтметр U, В | 5,55 | 5,60 | 5,68 |
| 5. Амперметр I, А | 1,00 | 1,25 | 1,50 |
6. Мощность 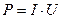 , Ватт , Ватт
| 5,55 | 7,00 | 8,44 |
7. Амплитуда импульса напряжения по осциллограмме 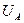 , В , В
| 25,00 | 25,00 | 27,50 |
8. Амплитуда импульса тока по осциллограмме 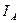 , А , А
| 177,80 | 182,20 | 200,0 |
9. Среднее напряжение по осциллограмме 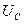 , В , В
| 0,13 | 0,14 | 0,12 |
10. Средний ток по осциллограмме 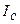 , А , А
| 0,94 | 0,98 | 1,20 |
11. Средняя мощность 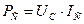 , Вт , Вт
| 0,13 | 0,18 | 0,18 |
12. Удельная мощность по осциллограмме 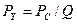 , Вт.ч/литр , Вт.ч/литр 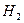
| 0,11 | 0,11 | 0,10 |
Сравнивая результаты экспериментов, представленные в табл. 12 и 13, видим, что удельные затраты энергии на получение водорода из воды зависят, главным образом от скважности импульсов напряжения и тока. С увеличением скважности импульсов напряжения с 2,70 (табл. 12) до 220 (табл. 13) расход энергии на получение водорода из воды уменьшается почти на порядок.
А теперь представим, что сделан электромеханический (ЭМГИ) аналог для питания по схеме, представленной на рис. 68. При скважности импульсов равной S=100, и их треугольной форме магниты будут занимать одну 1/50 контура окружности ротора. Вполне естественно, что энергия на формирование импульсов напряжения, подобных импульсам на рис. 69 уменьшится, примерно, в 50 раз. Теперь подключаем импульсную нагрузку с той же величиной тока 1,30 А.
Средняя величина напряжения (рис. 69) будет равна амплитуде импульса напряжения, делённой на скважность импульсов. Средняя величина тока (рис. 69) также будет равна амплитуде импульса тока, делённой на скважность импульсов. Вполне естественно, что средняя мощность будет равна произведению средних значений напряжения и тока (90) Это значит, что нагрузка на валу такого генератора увеличится на величину, равную произведению средней величины напряжения на среднюю величину тока. Её можно определить и путём деления произведений амплитудных значений напряжения и тока на скважности их импульсов (91). Если же мы разделим произведение амплитудных значений напряжения и тока на скважность один раз (32), то это будет означать, что электромеханический генератор генерирует напряжение не в узком секторе, а по всему контуру окружности ротора.
Изложенное даёт нам право заменить второй закон Кирхгофа законом формирования мощности в любом сечении электрической цепи: величина мощности в любом сечении электрической цепи равна произведению величины среднего напряжения в этом сечении на величину среднего тока.
Таким образом, экспериментально доказано, что прямые затраты энергии на электролиз воды существующими электролизерами значительно меньше тех, что показывают счётчики электроэнергии, учитывающие её потребление электролизёрами. Значит, энергии связи между атомами кислорода и водорода в молекуле воды значительно отличаются от тех энергий, которые мы получаем, взяв за основу расход энергии на кубический метр водорода, равный 4 кВтч.
В соответствии с данными, представленными в табл. 12 и 13, реальные энергии связи между атомами водорода и кислорода в молекуле воды можно принять в 10 раз меньшими, чем считалось до сих пор.
Поскольку при электролизе воды выделяется примерно 2/3 водорода и 1/3 кислорода, то расход энергии на получение одного кубометра водорода с учетом принятой величины составит примерно 0,40 кВтч или 3600х0,4=1440кДж. Один кубический метр содержит 1000/22,4=44,64 молей водорода. Тогда затраты энергии на получение одного моля водорода составят 1440/44,64=32,26 кДж, а на одну молекулу
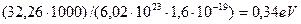 . (92)
. (92)
Так как в молекуле воды один атом кислорода и два атома водорода, то она имеет две связи. Энергия одной связи будет равна 0,34/2=0,17eV и мы можем определить энергетический уровень электрона атома водорода, на котором он находится в момент отделения от атома кислорода при электролизе воды.
Согласно спектру атома водорода (Приложение 1) электрон атома водорода имеет энергию связи с ядром, равную 0,17eV, находясь на девятом энергетическом уровне.
Если эта энергия соответствует реальности, то затраты энергии для получения моля водорода окажутся такими
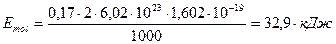 . (93)
. (93)
Затраты энергии на один кубический метр водорода составят 32,9х22,4=736,96 кДж или 736,96/3600=0,2 кВтч. На один литр водорода затраты электрической энергии составят примерно 0,20 Втч. Это соответствует эксперименту (табл. 13, строка 11).
Известно, что с увеличением температуры энергия связи между атомом кислорода и атомами водорода в молекуле воды уменьшается и они могут разделяться на водород и кислород. Если величина 0,20 Втч/л соответствует процессу диссоциации молекул воды, то мы можем определить температуру, при которой начинается процесс, эквивалентный рассмотренному.
Из приведенных расчетов следует, что величина 0,20 Вт/л соответствует энергии связи между атомами водорода и кислорода в молекуле воды равной 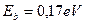 , а энергия фотона, разрушающего эту связь
, а энергия фотона, разрушающего эту связь 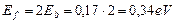 , а длина его волны будет равна
, а длина его волны будет равна
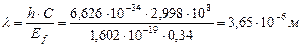 . (94)
. (94)
Эта длина волны фотона соответствует инфракрасному диапазону. Тогда температура 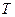 среды, при которой начинается процесс диссоциации молекул воды, определится по формуле
среды, при которой начинается процесс диссоциации молекул воды, определится по формуле
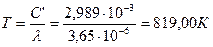 (95)
(95)
или
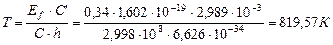 (96)
(96)
Величина этой температуры по шкале Цельсия равна 819,57-237,15=546,42 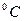 , что близко к её справочному значению [49].
, что близко к её справочному значению [49].
Конечно, молекула воды в этот момент находится под термическим напряжением, которое при электролизе заменяется электростатическим напряжением, формируемым постоянным потенциалом 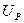 (рис. 63).
(рис. 63).
Мы вплотную подошли к анализу энергетики процесса разложения воды на водород и кислород при фотосинтезе, который идет под действием тепловых инфракрасных фотонов. Изложенная информация показывает, что для получения одного литра водорода достаточно 0,20 Втч электроэнергии. Если вести электролиз при напряжении 2 Вольта на ячейку, то средняя величина тока при этом составит 0,20/2=0,10А. Дальше мы увидим, что эта величина близка к величине тока, сопровождающего процесс электролиза воды при фотосинтезе.
Таким образом, эксперимент показывает, что прямые затраты энергии на электролиз воды, то есть затраты энергии без учета потерь, примерно, в 5,25/0,1= 52,5 раз меньше, чем у лучших современных промышленных электролизёров. Это создаёт предпосылки для поиска резервов снижения затрат энергии на электролиз воды, не путем совершенствования самого электролизёра, а путем совершенствования источника его питания.
5. 4. Низкоамперный электролиз воды
Низковольтный процесс электролиза воды известен со времен Фарадея. Он широко используется в современной промышленности. Рабочим напряжением между анодом и катодом электролизера является напряжение 1,6-2,3 Вольта, а сила тока достигает десятков и сотен ампер. В соответствии с законом Фарадея, затраты энергии на получение одного кубического метра водорода в этом случае составляют около 4 кВтч/ 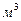 [40]. Минимальное напряжение, при котором начинается процесс электролиза воды, равно 1,23 В [49].
[40]. Минимальное напряжение, при котором начинается процесс электролиза воды, равно 1,23 В [49].
Возникает вопрос: как же идёт электролиз воды при фотосинтезе, когда явно отсутствует источник электроэнергии? Есть основания полагать, что при фотосинтезе молекула водорода выделяется из кластера воды (рис. 70, а и b) в синтезированном состоянии без использования электронов от постороннего источника электроэнергии.
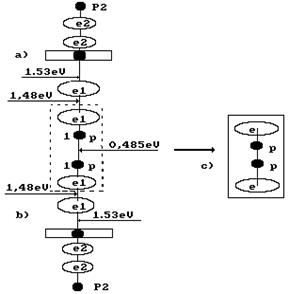
Рис. 70. Схема формирования второй структуры молекулы ортоводорода в структуре кластера из двух молекул воды (0,485 eV – энергия разрыва кластера воды при её испарении)
Функцию первичного источника энергии при фотосинтезе выполняют фотоны, поглощаемые валентными электронами и ослабляющими связи между электронами молекулы ортоводорода и электронами гидроксилов 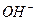 , которые формируются в кластерах воды (рис. 70). В результате молекула ортоводорода выделяется из такого кластера в синтезированном состоянии (рис. 70, с).
, которые формируются в кластерах воды (рис. 70). В результате молекула ортоводорода выделяется из такого кластера в синтезированном состоянии (рис. 70, с).
После выделения молекулы ортоводорода из кластера воды электроны молекул ортоводорода вступают в связь с валентными электронами других атомов и образуются молекулы других химических соединений. Например, молекулы бензола (рис. 71).
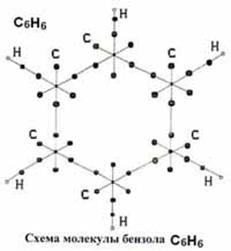
Рис. 71. Структура молекулы бензола
В результате молекула водорода разделяется на атомы водорода в условиях отсутствия фазы свободного состояния атомов водорода, которые существуют в плазменном состоянии при температуре до 10000С.
В описанном случае процесс выделения молекулы водорода из кластеров молекул воды идёт без электронов, получаемых из катода. Именно этот процесс электролиза идёт при фотосинтезе и мы попытаемся смоделировать его в техническом устройстве. А сейчас рассмотрим детали процесса выделения молекул водорода из кластера, состоящего из молекулы воды 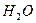 и иона
и иона 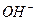 в электрическом поле электролизёра (рис. 72).
в электрическом поле электролизёра (рис. 72).
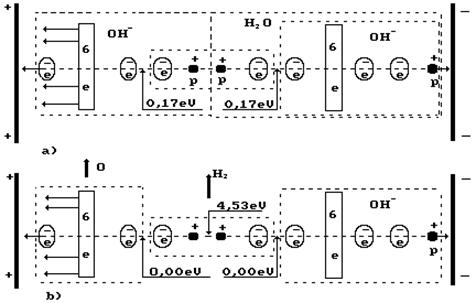
Рис. 72. Схема процесса низкоамперного электролиза
На рис. 72 показан анод слева, а катод справа. Протон Р атома водорода в молекуле воды ориентирован к катоду, а другой протон этой молекулы соединяется с протоном иона 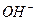 (слева). В результате образуется кластерная цепочка, с правой стороны которой расположена молекула воды
(слева). В результате образуется кластерная цепочка, с правой стороны которой расположена молекула воды 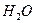 (рис. 50), слева - ион
(рис. 50), слева - ион 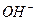 (рис. 52, а), а в центре - молекула ортоводорода
(рис. 52, а), а в центре - молекула ортоводорода 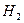 (рис. 53, а, b).
(рис. 53, а, b).
Обратим внимание на то, что осевой электрон атома кислорода и шесть кольцевых электронов иона 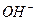 притягиваются к аноду одновременно (рис. 72, а слева). Электростатические силы, притягивающие шесть кольцевых электронов к аноду, деформируют электростатическое поле так, что осевой электрон приближается к ядру атома кислорода, а шесть кольцевых электронов удаляются от ядра атома. В этом случае энергии связи между протонами и электронами в сформировавшейся таким образом молекуле водорода распределяются так, что энергия связи между атомами водорода в его молекуле увеличивается до 4,53 eV, а между электронами атомов кислорода в ионах
притягиваются к аноду одновременно (рис. 72, а слева). Электростатические силы, притягивающие шесть кольцевых электронов к аноду, деформируют электростатическое поле так, что осевой электрон приближается к ядру атома кислорода, а шесть кольцевых электронов удаляются от ядра атома. В этом случае энергии связи между протонами и электронами в сформировавшейся таким образом молекуле водорода распределяются так, что энергия связи между атомами водорода в его молекуле увеличивается до 4,53 eV, а между электронами атомов кислорода в ионах 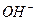 и электронами атомов водорода становятся равными нулю и молекула водорода выделяется из кластерной цепочки. Два атома кислорода образуют его молекулу, и она также выделяется.
и электронами атомов водорода становятся равными нулю и молекула водорода выделяется из кластерной цепочки. Два атома кислорода образуют его молекулу, и она также выделяется.
Таким образом, в электролитическом растворе под действием электростатического поля формируются сложные кластерные цепочки со строгой ориентацией между анодом и катодом [41]. Под действием электрического поля кластерная цепочка удлиняется, одновременно изменяются и энергии связи между элементами такой цепочки. Если мы возьмём за основу результаты эксперимента, приведенные на рис. 72, а, то минимальная энергия (≈4 Вт), при которой идет процесс электролиза, приведенная к энергии связи (0,17 eV) между электронами иона 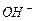 в цепочке (рис. 72, а) и молекулы воды, оказывается порядка 0,17 eV. Две таких связи дают энергию 0,34 eV, что меньше энергии 0,485 eV , при которой кластер из двух молекул разрывается при испарении молекул воды. Кроме этого, формирование молекулы ортоводорода увеличивает энергию связи между атомами водорода с 0,485 eV до 4,53 eV. Энергии связи 0,17 eV (рис. 72, а) уменьшаются до нуля (рис. 72, b) и сформировавшаяся молекула ортоводорода оказывается свободной.
в цепочке (рис. 72, а) и молекулы воды, оказывается порядка 0,17 eV. Две таких связи дают энергию 0,34 eV, что меньше энергии 0,485 eV , при которой кластер из двух молекул разрывается при испарении молекул воды. Кроме этого, формирование молекулы ортоводорода увеличивает энергию связи между атомами водорода с 0,485 eV до 4,53 eV. Энергии связи 0,17 eV (рис. 72, а) уменьшаются до нуля (рис. 72, b) и сформировавшаяся молекула ортоводорода оказывается свободной.
Конечно, это упрощенная схема. При более сложном процессе возможно формирование молекул перекиси водорода перед образованием молекулы кислорода. Именно к этому приводит малейшее нарушение оптимального сочетания параметров процесса электролиза.
Рассмотрим теперь реакции, протекающие у анода. Известно, что ион гидроксила (рис. 72, а), имея отрицательный заряд 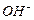 , движется к аноду (рис. 72, а). Два иона гидроксила, отдавая по одному электрону аноду и, соединяясь, друг с другом, образуют перекись водорода
, движется к аноду (рис. 72, а). Два иона гидроксила, отдавая по одному электрону аноду и, соединяясь, друг с другом, образуют перекись водорода 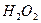 (рис. 72, b).
(рис. 72, b).
Известно, что процесс образования перекиси водорода эндотермический, а молекулы кислорода - экзотермический. При получении одного кубического метра водорода процесс образования перекиси водорода поглощает 22,32х109,00=2432,88 кДж. В силу этого даже при плазмоэлектролитическом процессе температура раствора в зоне анода остаётся низкой.
Если бы существовал процесс синтеза молекул кислорода, то при получении одного кубического метра водорода в зоне анода выделилось бы 22,32х495,00=11048,40 кДж. Вычитая из этой величины энергию, поглощенную при синтезе перекиси водорода, получим 11048,40-2432,88=8615,52 кДж. Складывая эту энергию с энергией синтеза молекул водорода 19463,00 кДж, получим 28078,52 кДж. В этом случае общий показатель тепловой энергетической эффективности 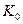 должен быть таким
должен быть таким 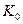 =28078,52/14400=1,95. Поскольку в реальности этой энергии нет, то этот факт подтверждает гипотезу об отсутствии процесса синтеза молекул водорода в зоне катода и молекул кислорода в зоне анода при низковольтном электролизе. Молекула водорода (рис. 72, b) и атом кислорода (рис. 72, b) формируются в кластерных цепочках до выделения их в свободное состояние, поэтому и не генерируется энергия их синтеза.
=28078,52/14400=1,95. Поскольку в реальности этой энергии нет, то этот факт подтверждает гипотезу об отсутствии процесса синтеза молекул водорода в зоне катода и молекул кислорода в зоне анода при низковольтном электролизе. Молекула водорода (рис. 72, b) и атом кислорода (рис. 72, b) формируются в кластерных цепочках до выделения их в свободное состояние, поэтому и не генерируется энергия их синтеза.
После передачи двумя ионами гидроксила двух электронов аноду (рис. 72, а) образуется молекула перекиси водорода (рис. 72, b), которая, распадаясь, образует молекулу кислорода (рис. 72, с) и два атома водорода; последние, соединяясь с ионами гидроксила, образуют две молекулы воды (рис. 72, d,e). С учетом этого химическая реакция в зоне анода запишется так
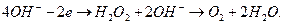 (97)
(97)
А теперь опишем результаты экспериментов, показывающих связь, новой теории электролиза воды с реальностью.
5.5. Экспериментальная проверка гипотезы низкоамперного электролиза воды
Известно, что при фотосинтезе поглощается углекислый газ 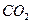 . Считается, что углерод
. Считается, что углерод  молекулы
молекулы 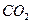 идет на построение клеток растений, а кислород
идет на построение клеток растений, а кислород 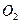 выделяется [1]. Теперь у нас есть основания усомниться в этом и предположить, что молекула
выделяется [1]. Теперь у нас есть основания усомниться в этом и предположить, что молекула 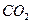 целиком используется на построение клеток растений. Кислород же выделяют молекулы воды и он уходит в атмосферу, а атомы водорода молекул воды используются в качестве соединительных звеньев молекул, из которых строятся клетки растений [2].
целиком используется на построение клеток растений. Кислород же выделяют молекулы воды и он уходит в атмосферу, а атомы водорода молекул воды используются в качестве соединительных звеньев молекул, из которых строятся клетки растений [2].
Возникает вопрос: а нельзя ли смоделировать электролитический процесс разложения воды на водород и кислород, который идет при фотосинтезе? Анализ структуры молекулы воды (рис. 71), выявленной нами, показывает возможность электролиза воды при минимальном токе. На рис. 71 представлена схема молекулы воды с энергиями связи между атомами водорода и кислорода в условиях, когда молекула воды находится в нейтральной среде, без ионов щелочи или кислоты, а также без электрического потенциала, который бы действовал на такие ионы [2].
Протоны атомов водорода в молекулах воды могут соединяться между собой и образовывать кластеры. В результате в цепи кластера образуется молекула ортоводорода (рис. 70, b и 71, а, b, c) [2].
Поиск условий моделирования процесса разложения воды на водород и кислород, который идет при фотосинтезе, привел нас к простой конструкции ячейки, в которой имитированы годовые кольца стволов деревьев в виде зазоров между коническими электродами (рис. 72).
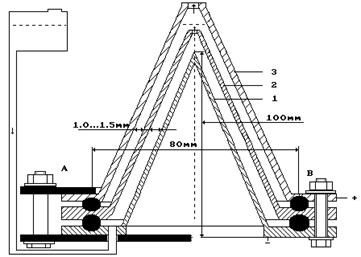
Рис. 72. Низкоамперный электролизер (Пат. № 2227817)
Оказалось, что процесс электролиза может протекать при напряжении 1,5-2,0 В между анодом и катодом и средней силе тока 0,02 А. Поэтому этот процесс назван низкоамперным.
Прежде всего, отметим, что материал анода и катода один – сталь, что исключает возможность формирования гальванического элемента. Тем не менее, на электродах ячейки появляется разность потенциалов около 0,1В при полном отсутствии электролитического раствора в ней. После заливки раствора разность потенциалов увеличивается. При этом положительный знак заряда всегда появляется на верхнем электроде, а отрицательный – на нижнем. Если источник постоянного тока генерирует импульсы, то выход газов увеличивается [2].
Поскольку лабораторная модель ячейки низкоамперного электролизёра генерирует небольшое количество газов, то самым надёжным методом определения их количества является метод определения изменения массы раствора за время опыта и последующего расчета выделившегося водорода и кислорода.
Для дальнейших расчётов необходимо иметь информацию о плотности водорода при различной температуре. Она представлена в табл. 14 [49].
Таблица 14. Плотность водорода при разной температуре
| Температура, град. Цельсия | Плотность, гр./литр |
| 0,0 | 0,0896 |
| 20,0 | 0,0846 |
| 25,0 | 0,0814 |
| 100,0 | 0,0661 |
| 500,0 | 0,0317 |
Примем плотность, соответствующую  С и равную 0,0846 гр. /л и повторим ещё раз расчёт содержания водорода и кислорода в одном литре воды.
С и равную 0,0846 гр. /л и повторим ещё раз расчёт содержания водорода и кислорода в одном литре воды.
Известно, что грамм-атом численно равен атомной массе вещества, а грамм-молекула – молекулярной массе вещества. Например, грамм-молекула водорода в молекуле воды равна двум граммам, а грамм-атом атома кислорода – 16 граммам. Грамм-молекула воды равна 18 граммам. Так как масса водорода в молекуле воды составляет 2х100/18=11,11%, а масса кислорода – 16х100/18=88,89%, то это же соотношение водорода и кислорода содержится в одном литре воды. Это означает, что в 1000 граммах воды содержится 111,11 грамм водорода и 888,89 грамм кислорода.
Один литр водорода весит 0,0846 гр., а один литр кислорода -1,47 гр. Это означает, что из одного литра воды можно получить 111,11/0,0846=1313,36 литра водорода и 888,89/1,47=604,69 литра кислорода. Из этого следует, что один грамм воды содержит 1,31 литра водорода [44].
Затраты электроэнергии на получение 1000 литров водорода сейчас составляют 4 кВтч, а на один литр – 4 Втч. Поскольку из одного грамма воды можно получить 1,31 литра водорода, то на получение водорода из одного грамма воды сейчас расходуется 1,31х4=5,25 Втч.








