1.6. Энергия и мощность постоянного и переменного токов

Дата: 2025-05-21; Просмотры: 4

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Источники постоянного напряжения и тока родились первые. Источники переменного напряжения и переменного тока появились позже, и возникла проблема сравнения их электрической энергии и электрической мощности. К тому времени уже были вольтметры, которые измеряли величину постоянного напряжения и амперметры, которые измеряли величину постоянного тока. Вольтметры включались в электрическую сеть параллельно, а амперметры последовательно (рис. 13), но физическая суть электрических величин, названных Вольтами и Амперами, до сих пор остаётся в тумане.

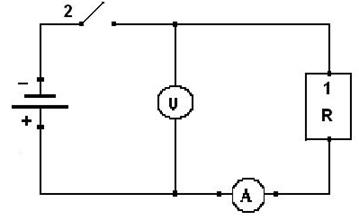
Рис. 13. Схема включения вольтметра V и амперметра А в электрическую цепь

Вольтметр 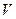фиксирует величину постоянного напряжения 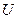. Напряжение, поданное потребителю, формирует ток 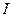. Его величину измеряет амперметр 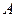. Если напряжение и ток непрерывны, то на клеммах потребителя фиксируется величина электрической энергии 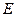, равная произведению напряжения 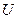на величину тока 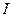и на время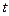

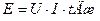. (12)

Чтобы иметь представление о величине энергии, генерируемой в одну секунду, введено понятие мощность. Она определяется по формуле [1]

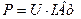. (13)

Появление переменного тока значительно усложнило процесс измерения электрической энергии и мощности. Так как переменное напряжение и переменный ток изменяются синусоидально, то для определения средней мощности надо интегрировать функции изменения напряжения и тока в интервале периода 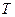их изменения и формула для расчёта средней мощности 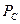становится такой

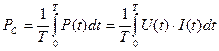. (14)

,

Нетрудно видеть (рис. 11), что при синусоидальном изменении напряжения и тока средняя мощность в интервале периода 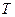их изменения будет равна нулю. Из этого следует, что произведение средних значений переменного напряжения и переменного тока не может служить критерием для расчёта мощности переменного тока. В качестве такого критерия надо было выбрать конечный результат действия напряжения и тока. Так как электролитические процессы протекают только при постоянном напряжении, то электролитический результат действия тока тоже не может быть критерием достоверности средней мощности, генерируемой переменным напряжением и переменным током. Оказалось, что роль такого критерия может выполнять тепло, выделяемое при действии тока. В результате надо было найти параметры переменного напряжения и тока, которые генерируют такое же количество тепла, как и эквивалентные им величины постоянного напряжения и постоянного тока.

Количество тепла 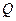, выделяемое постоянным током 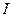на сопротивлении 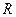за время 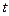, равно

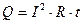. (15)

Квадрат переменного тока 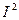позволяет учитывать его положительные и отрицательные значения (рис. 14). Тогда среднее значение квадрата силы синусоидального переменного тока 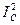за период 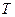можно определить по формуле

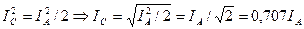. (16)

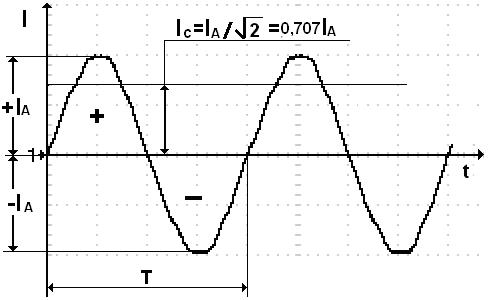
Рис. 14. Синусоидальное изменение переменного тока

Аналогично определяется и средняя величина переменного напряжения, равная .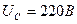

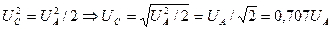. (17)

,

Из этого следует амплитудное значение средней величины переменного напряжения (220В), равное

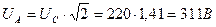. (18)

Из этого следует, что средняя величина мощности переменного напряжения и тока определится по формуле

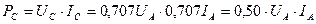(19)

А теперь отметим, что импульсная энергетика пока базируется на постоянном напряжении и постоянном токе, поэтому мы пока не будем касаться характеристик средних величин переменного напряжения 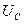(17) и переменного тока 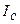(16) и средней величины переменной мощности 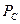(19).

1.7. Принципы работы электромоторов и электрогенераторов

Принципы работы электромотора и электрогенератора были открыты Майклом Фарадеем в начале 19-го века. Считается, что в его опытах наглядно проявилась связь между электрическими и магнитными явлениями. Однако, сейчас мы покажем, что эта наглядность оказалась ошибочной. Проводник с током перемещается в магнитном поле постоянного магнита не в результате взаимодействия электрического поля с магнитным, а в результате взаимодействия магнитного поля постоянного магнита и магнитного поля вокруг проводника, формируемого движущимися в нём электронами [1].

Чтобы понять это, надо разобраться с процессом взаимодействия магнитных силовых линий, формируемых обычными стержневыми постоянными магнитами (рис. 15).

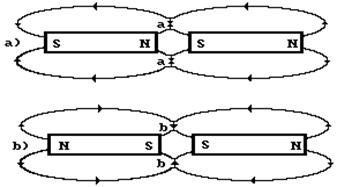
Рис. 15. Схема взаимодействия магнитных силовых линий стержневых магнитов

Как видно (рис. 15, а), у разноименных магнитных полюсов, сближающих друг друга, магнитные силовые линии в зоне контакта полюсов (рис. 15, а, точки а) направлены навстречу друг другу 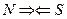, а у одноименных магнитных полюсов, отталкивающих друг друга (рис. 15, b, точки b), направления магнитных силовых линий в зоне контакта полюсов совпадают 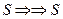[1].

Из описанного процесса взаимодействия магнитных полюсов постоянных магнитов следует, что если у двух параллельных проводов ток будет течь в одном направлении (рис. 16, а), то силовые линии магнитных полей, формирующихся в плоскости, перпендикулярной проводам, в зоне их контакта будут направлены навстречу друг другу и провода будут сближаться, как разноименные полюса магнитов (рис. 15, а) [1].

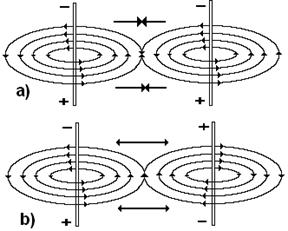
Рис. 16. Схема взаимодействия магнитных полей параллельных проводников с током

Если же направление тока у параллельных проводов будет противоположно (рис. 16, b), то направления магнитных силовых линий образующихся при этом магнитных полей будут совпадать по направлению в зоне их контакта и такие провода будут удаляться друг от друга, как и одноименные полюса стержневых магнитов (рис. 16, b) [1].

А теперь обратим внимание на взаимодействие силовых линий магнитного поля постоянного магнита с силовыми линиями магнитного поля, формируемого электронами, движущимися от плюса к минусу по проводнику (рис. 17). В зоне D силовые линии направлены навстречу друг другу, поэтому они сближаются, как и силовые линии магнитных полей двух проводников с равнонаправленным током (рис. 16, а). В результате возникает сила 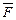, смещающая проводник влево (рис. 17).

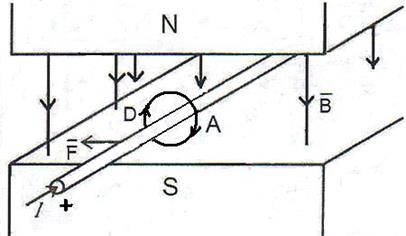
Рис. 17. Схема движения проводника с током в магнитном поле

С другой стороны проводника, в зоне А, направления силовых линий постоянного магнита и магнитного поля, сформированного движущимися по проводнику электронами, совпадают по направлению. В этом случае, как следует на рис. 16, b, силовые линии отталкиваются и также формируют силу, направленную влево. Так формируется суммарная сила, перемещающая проводник с током в магнитном поле [1].

Как видно, перемещение проводника происходит в результате взаимодействия магнитных полей постоянного магнита и проводника с током. Нет здесь взаимодействия электрического и магнитного полей, на котором базируется теория всей современной электротехники. Из этого следует, что нет здесь места и уравнениям Максвелла, из которых следует, что перемещение проводника с током в магнитном поле – следствие меняющихся напряженностей электрических и магнитных полей, о которых упоминает Е.А. Ильина [1]. Проводник движется в результате взаимодействия только магнитных полей.

Если же в магнитном поле движется проводник без тока (рис. 18), то в нём генерируется напряжение. Внешнее магнитное поле ориентирует свободные электроны в проводнике так, чтобы магнитные силовые линии их суммарного магнитного поля вокруг проводника формировали сопротивление его перемещению (рис. 18).

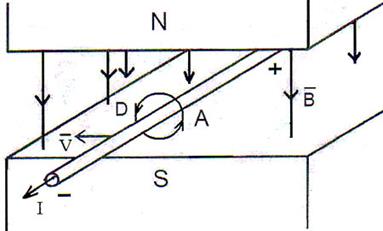
Рис. 18. Схема генерирования тока в проводнике, движущемся в магнитном поле

Движение электронов вдоль проводника (рис. 18) от плюса к минусу возникает благодаря принудительному перемещению проводника со скоростью 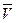в магнитном поле постоянного магнита в левую сторону. В зоне D магнитные силовые линии постоянного магнита и магнитные силовые линии проводника с током направлены в одну сторону и будут отталкиваться друг от друга, препятствуя перемещению провода в левую сторону. В зоне А указанные силовые линии будут направлены навстречу друг другу и будут сближаться и также препятствовать перемещению провода в левую сторону (рис. 18). Из этого следует, что перемещение электронов вдоль провода от плюса к минусу возможно только при принудительном перемещении провода в левую сторону [1].

Таким образом, работа электромоторов и электрогенераторов базируется на взаимодействии только магнитных полей, но не магнитных и электрических, как считалось ранее.

Из изложенного следует, что переменное магнитное поле вокруг проводника формируют электроны, движущиеся в нём. Зная детали процессов этих движений, можно управлять формированием магнитных полей вокруг проводников и таким образом заставлять ротор электрогенератора вращаться без постороннего привода. Первый такой генератор был изготовлен и испытан нами в 2010г (рис. 19).

Рис. 19. Первый в мире электромотор-генератор МГ-1

Роль мотора у МГ-1 выполняет ротор, а роль генератора статор. Это первый в мире потребитель электрических импульсов и одновременно генератор электрических импульсов – основа будущей импульсной энергетики. Дальше мы детально опишем итоги его испытаний.

1.8. Принцип работы диода

Ортодоксальная физика не имеет приемлемого варианта объяснения принципа работы диода. Он проясняется лишь при наличии модели электрона и знания законов его поведения в проводах с постоянным и переменным напряжением, которые мы уже описали.

Существующая интерпретация работы полупроводников и диодов базируется на понятии дырочной проводимости. Приводим текст определения понятия «дырка» из Физического энциклопедического словаря. М. «Советская энциклопедия» 1984г. 186с. «…..Дырка – положительный заряд 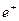, имеющий энергию, равную энергии отсутствующего электрона с обратным знаком».

Странное определение. Но надо учитывать, что это были первые представления о сути работы полупроводников. Теперь у нас есть возможность глубже проникнуть в эту суть. Для этого надо воспользоваться принципом последовательности анализа этого сложного явления.

Поскольку диод пропускает одни электроны и задерживает другие, то он делает это, учитывая два различных свойства электрона, а в заряде электрона заложено только одно свойство – отрицательный заряд. Поэтому надо включить в анализ поведения электрона в диоде и другие его характеристики. Так как электрон имеет отрицательный заряд и два магнитных полюса: северный и южный, то именно они и позволяют диоду выполнить функцию пропуска одних электронов и задержки других (рис. 20) [1].

В этом случае сохраняются представления о дырочной проводимости, если дырки, пропускающие и задерживающие электроны, наделить одноимённой магнитной полярностью (рис. 20).

Рис. 20. а) схема пропуска диодом электронов, имитирующих положительное напряжение;

b) схема задержки электронов, имитирующих отрицательное напряжение

Теперь нам известно, что электроны не имеют орбитальных движений в атомах. Они связаны с протонами ядер линейно. Поскольку протон тоже имеет северный и южный магнитные полюса, то возможна такая совокупность компоновки магнитных полюсов нейтронов, протонов и электронов, при которой на поверхности атома окажутся электроны, на внешней поверхности которых будут, например, южные магнитные полюса. Далее, возможно формирование таких молекул из этих атомов, которые создавали бы дырку, периметр которой и формировал бы дискретные магнитные поля одной полярности, например, южной (рис. 20, a).

Мы уже показали, что положительное напряжение соответствует ориентации электронов в проводе, показанной на рис. 20, a (слева). В этом случае к дырке диода с магнитным барьером, сформированным южными магнитными полюсами S атомов материала диода, подходят электроны с северными магнитными полюсами N, совпадающими с направлением движения этих электронов. Вполне естественно, что дырка диода с южным магнитным барьером пропустит электроны, пришедшие к ней со своими северными полюсами. Так электроны, формирующие напряжение с положительной частью амплитуды синусоиды, пройдут через диод (рис. 21).

Во второй половине периода изменения направления векторов магнитных моментов и спинов электронов у диодной дырки окажутся электроны с южными магнитными полюсами, направленными в сторону их движения (рис. 20, b). Вполне естественно, что диодный барьер, сформированный из южных магнитных полюсов электронов атомов, не пропустит такие электроны. Неудачливым электронам придётся ждать ещё пол периода и они окажутся повернутыми к диодной дырке северными магнитными полюсами и она пропустит их, как своих, а величина напряжения в момент, когда электроны в проводе были повернуты к диоду южными магнитными полюсами, будет равна нулю (рис. 20, b и 21) [1].

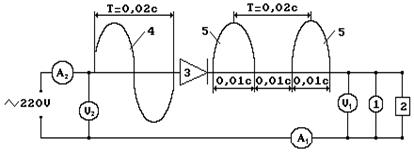
Рис. 21. Схема формирования диодом выпрямленного напряжения

Описанная закономерность работы диода следует из эксперимента, схема которого представлена на рис. 21. Обратим внимание на простоту электрической схемы рассматриваемого эксперимента. В ней нет ни ёмкости, ни индуктивности.

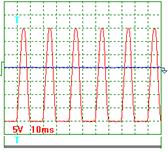Рис. 22. Напряжение

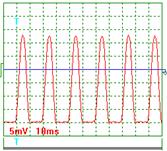Рис. 23. Ток

Осциллограммы напряжения и тока, выпрямленные диодом, показаны на рис. 22 и 23. Как видно, диод пропускает положительные значения переменного напряжения (рис. 22) и переменного тока (рис. 23), когда электроны, подошедшие к дырке, оказываются повернутыми к ней северными магнитными полюсами (рис. 20, а) и не пропускает отрицательные составляющие напряжения и тока, когда электроны оказываются повернутыми к дыркам южными магнитными полюсами (рис. 20, b).

1.9. Зарядка диэлектрического конденсатора

Ошибочность существующей интерпретации работы конденсатора особенно очевидна. Она базируется на присутствии в электрической цепи положительных и отрицательных зарядов. Носители этих зарядов известны: протон и электрон. Однако, также известно, что они чувствуют присутствие друг друга на расстоянии в тысячу раз большем размера электрона и в миллион раз большем размера протона [1]. Даже такое их далёкое соседство заканчивается процессом формирования атомов водорода, которые существуют лишь в плазменном состоянии при температуре до 10000С. Это происходит, например, в процессах удаления электронов и протонов от Солнца и последующего объединения их в атомы водорода. Так что совместное присутствие протонов и электронов в свободном состоянии в проводниках полностью исключается, поэтому положительный и отрицательный потенциалы на пластинах диэлектрического конденсатора – ошибка физиков. Исправим её.

Сейчас мы увидим, что пластины диэлектрического конденсатора заряжаются не разноимённой электрической полярностью, а разноимённой магнитной полярностью. При этом функции плюса принадлежат южному магнитному полюсу электрона, а функции минуса – северному (рис. 1). Эти полюса и формируют полярность, но не электрическую, а магнитную. Проследим процесс зарядки диэлектрического конденсатора, чтобы увидеть, как магнитные полюса электрона формируют магнитную полярность его пластин. Известно, что между пластинами диэлектрического конденсатора находится диэлектрик D (рис. 24).

Схема эксперимента по зарядке диэлектрического конденсатора показана на рис. 24. Самое главное требование к схеме – ориентация её с юга (S) на север (N). Чтобы обеспечить полную изоляцию конденсатора от сети после его зарядки, желательно использовать электрическую вилку, включаемую в розетку сети с напряжением 220 V.

Сразу после диода d показан компас 1 (К), положенный на провод, идущий к конденсатору С. Стрелка этого компаса, отклоняясь вправо в момент включения вилки, показывает направление движения электронов (рис. 24) от точки S к нижней пластине конденсатора. Тут уместно обратить внимание на общность информации о поведении электронов в проводах, представленной на рис. 7, 8, 10, 12, 16 и 24.

Выше компаса 1 (рис. 24) показана схема направления магнитного поля вокруг провода, формируемого движущимися в нём электронами. Эта схема аналогична схемам, показанным на рис. 8.

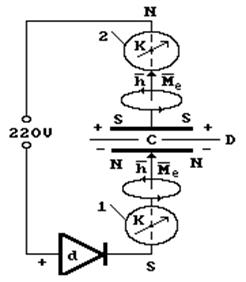
Рис. 24. а) схема нашего эксперимента зарядки конденсатора;

Таким образом, электроны, прошедшие через диод, приходят к нижней пластине конденсатора, сориентированными векторами спинов 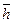и магнитных моментов 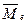к её внутренней поверхности (рис. 24). В результате на этой поверхности формируется северный магнитный потенциал (N).

Вполне естественно, что к внутренней поверхности верхней пластины конденсатора электроны придут из сети сориентированными южными магнитными полюсами (S). Доказательством этого служит экспериментальный факт отклонения стрелки верхнего компаса 2 (К) вправо (рис. 24). Это означает, что электроны, движущиеся из сети к верхней пластине конденсатора, ориентированы южными магнитными полюсами (S) в сторону движения (рис. 25).

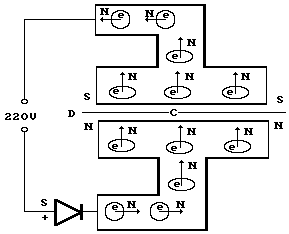
Рис. 25. Схема движения электронов к пластинам диэлектрического конденсатора

Таким образом, ориентацию электронов на пластинах диэлектрического конденсатора обеспечивает проницаемость их магнитных полей через диэлектрик D (рис. 25). Потенциал на пластинах конденсатора один – отрицательный и две магнитных полярности: северного и южного магнитных полюсов.

На рис. 25 представлена схема, поясняющая ориентацию электронов, движущихся к пластинам конденсатора С. Электроны приходят к нижней пластине конденсатора, сориентированными северными магнитными полюсами (N) к её внутренней поверхности (рис. 25). К внутренней поверхности верхней пластины конденсатора приходят электроны, сориентированные южными магнитными полюсами (S).

Так электроны – единственные носители электричества в проводах формируют на пластинах конденсатора не разноимённую электрическую полярность, а разноимённую магнитную полярность. Нет на пластинах диэлектрического конденсатора протонов – носителей положительных зарядов.

1.10. Разрядка диэлектрического конденсатора

Процесс разрядки диэлектрического конденсатора на сопротивление – следующее экспериментальное доказательство соответствия реальности выявленной модели электрона (рис. 1) и ошибочности сложившихся представлений о том, что на пластинах диэлектрического конденсатора формируются разноимённые электрические заряды (рис. 26) [1].

Схема отклонения стрелок компасов (К) 1, 2, 3 и 4 при разрядке конденсатора на сопротивление R в момент включения выключателя 5 показана на рис. 26.

Как видно (рис. 26), в момент включения процесса разрядки конденсатора, магнитная полярность на пластинах конденсатора изменяется на противоположную и электроны, развернувшись, начинают двигаться к сопротивлению R (рис. 26, 27).

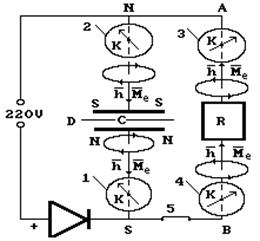
Рис. 26. Схема отклонения стрелок компасов (К) в момент разрядки конденсатора

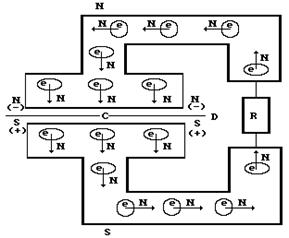
Рис. 27. Схема движения электронов от пластин конденсатора к сопротивлению R при

разрядке диэлектрического конденсатора

Электроны, идущие от верхней пластины конденсатора ориентируются южными магнитными полюсами в сторону движения, а от нижней – северными (рис. 26). Компасы 3 и 4, установленные на совокупности проводов ВА, сориентированных с юга на север, чётко фиксируют этот факт, отклонением стрелок вправо, доказывая этим, что векторы спинов и магнитных моментов всех электронов в этих проводах направлены с юга на север (рис. 26, 27).

1.11. Конденсатор + индуктивность

Конденсатор и индуктивность – основные элементы колебательных систем. Схематически они показываются просто (рис. 28) [1]. Считается, что одна пластина конденсатора С заряжена отрицательно, а другая положительно. Если конденсатор электролитический, то это соответствует реальности, так как указанные потенциалы формируют его ионы. Другое дело провод, по которому движутся электроны. В нём не могут присутствовать одновременно и электроны, и протоны, так как их соседство заканчивается образованием атомов водорода и плазмы с температурой до 10000 С [1].

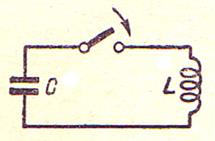
Рис. 28. Схема конденсатор + индуктивность

Таким образом, процессы, протекающие в конденсаторах и индуктивностях, а также проводах, которые соединяют их, остаются скрытыми для понимания. Попытаемся раскрыть эту таинственность. Для этого представим пластины конденсатора и провода, подходящие к ним, в увеличенном масштабе и разместим в них модели электронов 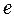(рис. 29). Катушку индуктивности представим в виде полутора витков и покажем направления движения электронов 1 и 2 в витках при разрядке конденсатора.

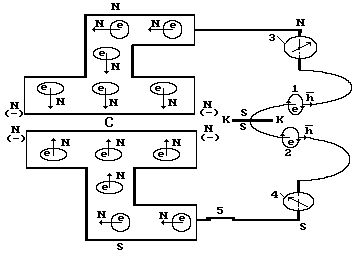
Рис. 29. Схема процессов движения электронов в цепи:

конденсатор – индуктивность при разрядке конденсатора

А теперь попытаемся найти ответ на главный вопрос электродинамики: в чём сущность причины, формирующей колебательный процесс изменения напряжения в системе конденсатор – индуктивность?

Чтобы найти ответ на поставленный вопрос, проследим за движением электронов к катушке индуктивности. Главное в этом процессе – направления движения электронов из конденсатора в катушку индуктивности. Мы уже показали, что эта задача решается вполне удовлетворительно с помощью древнейшего прибора – компаса. Установим эти приборы на провода, подходящие к катушке индуктивности, предварительно сориентировав их в направлении с юга на север (рис. 29).

Итак, проследим за движением электронов от конденсатора к катушке индуктивности вблизи клемм этой катушки. Обратим внимание на отличия в ориентации электронов в проводах, соединяющих конденсатор и актив,ное сопротивление (рис. 24, 26) и в проводах, соединяющих конденсатор и катушку индуктивности (рис. 29), зафиксированные отклонением стрелок компасов.

Теперь видно, что электроны от верхней и нижней пластин конденсатора встречаются в середине катушки индуктивности (сечение К-К) одноимёнными зарядами и одноимёнными южными магнитными полюсами. Это автоматически формирует процесс их отталкивания друг от друга и они устремляются вновь к пластинам конденсатора.

Когда конденсатор заряжен, то напряжение на его пластинах в момент включения выключателя 5 максимально и равно, например, 100 В (рис. 29, 30, а) [1].

Совокупность магнитных полей всех электронов во всех витках катушки (рис. 29) формирует суммарное магнитное поле, направление силовых линий которого легко определяется по направлению спинов 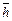электронов 1 и 2. Эти электроны подходят к сечению К-К с противоположно направленными векторами спинов и магнитных моментов. Это значит, что сформированные ими магнитные поля вокруг витков катушки в зоне встречи электронов (сечение К-К) направлены навстречу друг другу одноимёнными магнитными полюсами и тоже отталкиваются (рис. 29). Когда электроны, идущие от верхней и нижней пластин конденсатора С, встретятся в сечении К-К катушки, то конденсатор C полностью разрядится.

Итак, к моменту начала разрядки конденсатора напряжение U на его клеммах имеет максимальное значение (рис. 26, 30, а), ток I и напряжённость H магнитного поля катушки равны нулю (рис. 30, b). В момент прихода электронов к сечению К-К катушки и их остановки напряжение на клеммах конденсатора оказывается равным нулю (рис. 30, a), а величины тока и напряженности магнитного поля катушки – максимуму (рис. 30, b и c).

Далее, напряжённость магнитного поля катушки начинает уменьшаться (рис. 30, b) и автоматически изменяет направление векторов спинов и магнитных моментов электронов на противоположное и они, двигаясь назад к конденсатору, формируют на его клеммах противоположную магнитную полярность. В момент прихода электронов к пластинам конденсатора отрицательное напряжение на его клеммах достигает максимума (рис. 30, a), а величины обратно направленных тока и напряженности магнитного поля принимают нулевые значения (рис. 30, b и c).

После этого начинается второе движение электронов от пластин конденсатора к катушке. При этом электроны меняют направления векторов магнитных моментов и спинов на противоположные. В результате величина противоположного (отрицательного) потенциала на пластинах конденсатора начинает уменьшаться до нуля (рис. 30, a) а величина тока, обусловленная движением электронов с противоположно направленными векторами спинов, увеличиваясь, уходит в отрицательную зону (рис. 30, b). Так же изменяется и напряженность противоположно направленного магнитного поля катушки (рис. 30, c).

Когда электроны повторно придут к середине сечения К-К катушки, то напряжение на клеммах конденсатора станет равным нулю (рис. 30, a) а напряженность магнитного поля катушки, сформированная электронами с направлениями векторов спинов и магнитных моментов, противоположных первому приходу электронов к середине сечения К-К, и величина тока достигнут максимальных отрицательных значений (рис. 30, b и c). Так формируются синусоидальные законы изменения напряжения, тока и напряжённости магнитного поля в колебательном контуре: конденсатор + катушка индуктивности [1].

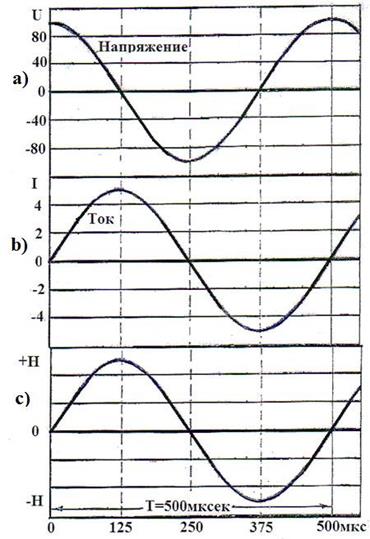
Рис. 30. Закономерность изменения напряжения, тока и напряжённости магнитного поля при разрядке конденсатора на катушку индуктивности (рис. 29)

Обратим внимание на то, что перезарядку конденсатора осуществляет один носитель электрического заряда – свободный электрон, без участия положительно заряженного протона, который не существует в проводах в свободном состоянии. Поэтому у нас нет никакого права приписывать пластинам конденсатора разную электрическую полярность. Они получают разную магнитную полярность.

Итак, у нас появилась возможность составить уравнения изменения напряжения U, тока I, и напряжённости Н магнитного поля в колебательном контуре конденсатор – катушка индуктивности. Поскольку в момент начала разрядки конденсатора напряжение U на его клеммах максимально, ток I и напряжённость магнитного поля Н минимальны, то уравнения их изменения запишутся так:

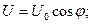(20)

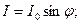(21)

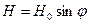. (22)

Это и есть исходные уравнения, заменяющие уравнения Максвелла при описании процессов, протекающих в колебательном контуре конденсатор + индуктивность.

Специалистам понятно, что при отсутствии информации о структуре электрона невозможно описать процесс работы колебательного контура: конденсатор - индуктивность. Этот процесс раскрывает свои тайны при анализе в нём поведения, выявленной и глубоко обоснованной нами модели электрона (рис. 1) [1].

А теперь отметим особо роль ЭДС самоиндукции, которая возникает в обмотках катушек сразу после разрыва электрической цепи, по которой в неё подаётся напряжение. Человек давно научился извлекать пользу из импульсов ЭДС самоиндукции, подавая их на свечи зажигания двигателей внутреннего сгорания. Но на этом извлечение пользы из этих импульсов остановилось. В большей части других электротехнических устройств появление ЭДС самоиндукции считается вредным явлением и с ним борются, вместо того, чтобы извлекать пользу. Причина такого отношения к импульсам ЭДС самоиндукции скрыта очень глубоко. Она – следствие фундаментальной физической ошибки, незамеченной математиками, решавшими проблему учёта расхода электрической энергии и, в частности – средней электрической мощности, реализуемой первичным источником питания в виде импульсов напряжения и тока. Поэтому освоение резервов импульсной энергетики начнём с анализа этой ошибки.

2. ГЛОБАЛЬНАЯ ФИЗИЧЕСКАЯ ОШИБКА МАТЕМАТИКОВ

И